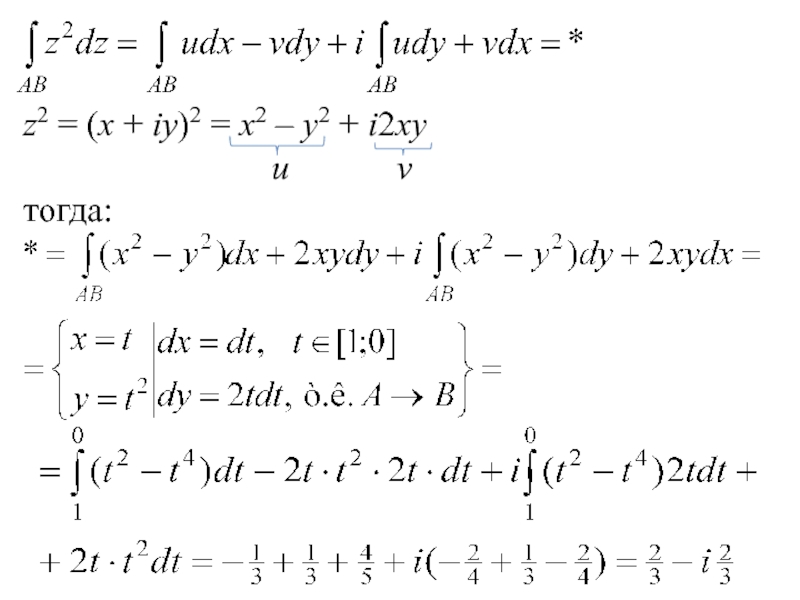Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 11 § 11.1. Интегрирование функции комплексного переменного. Пусть на
Содержание
- 1. Лекция 11 § 11.1. Интегрирование функции комплексного переменного. Пусть на
- 2. Слайд 2
- 3. и – действительные числа.x(t), y(t)
- 4. Они отвечает соответствующим комплексным числам.Пусть на комплексной
- 5. Определение. (Интеграла).Если существует предел интегральной суммыне зависящий
- 6. Теорема (о существовании интеграла от функции комплексного
- 7. Так как любую функцию комплексного переменного можно
- 8. Значит в использованном выражении (1), интегральная сумма
- 9. Так как f(z) непрерывна на L, то
- 10. Так как каждый из пределов входящий, входящий
- 11. Свойства интегралов от ФКП. Если L+ и
- 12. § 11.2. Понятие первообразной. Формула Ньютона-Лейбница. Интегрирование
- 13. Теорема (о первообразной)Если функция f(z) дифференцируема в
- 14. Замечание 2: Если f(z) непрерывна в односвязной
- 15. Теорема (Ньютона- Лейбница).Если f(z) дифференцируема в односвязной
- 16. Пример: Дана функция z2.Найти интеграл от z2по
- 17. z2 = (x + iy)2 = x2
- 18. 2-й способ решения с помощью формулы Ньютона-Лейбница:
- 19. § 11.3 Интегральная теорема КошиЕсли функция f(z)
- 20. Из аналитичности следует выполнение условий Коши-РиманаПусть L
- 21. Слайд 21
- 22. Скачать презентанцию
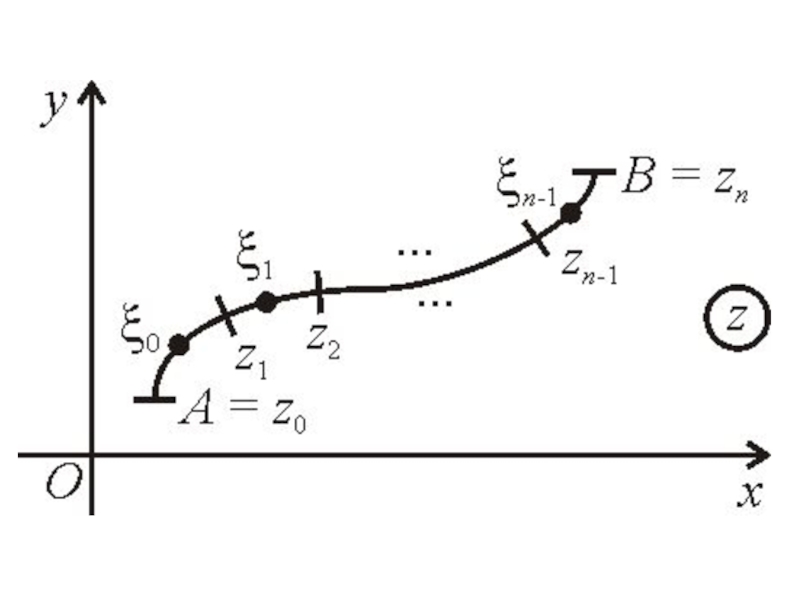
и – действительные числа.x(t), y(t) – действительные числа.Разобьем AB произвольным образом:Найдем разности двух составляющих комплексного числа.На каждом из участков выберем произвольные точки
Слайды и текст этой презентации
Слайд 1Лекция 11
§ 11.1. Интегрирование функции комплексного переменного.
Пусть на комплексной плоскости
задана кривая AB – ориентированная, незамкнутая, кусочно-гладкая, без самопересечений.
z(t) эквивалентно следующему:Слайд 3 и – действительные числа.
x(t), y(t) – действительные числа.
Разобьем
AB произвольным образом:
Найдем разности двух составляющих комплексного числа.
На каждом из
участков выберем произвольные точки Слайд 4Они отвечает соответствующим комплексным числам.
Пусть на комплексной плоскости, в том
числе и на дуге AB определена комплексная функция f(z). Найдем
ее значения в точках:и составим сумму вида: - это интегральная сумма.
Слайд 5Определение. (Интеграла).
Если существует предел интегральной суммы
не зависящий от способа разбиения
дуги AB и выбора точек , то этот
предел называют интегралом по дуге AB и обозначают:Слайд 6Теорема (о существовании интеграла от функции комплексного переменного).
Пусть функция f(x)
непрерывна на некоторой кривой L, которая является ориентируемой, кусочно-гладкой, незамкнутой,
тогда интеграл по дуге L от этой функции существует.Доказательство
Рассмотрим интегральную сумму
Слайд 7Так как любую функцию комплексного переменного можно представить в виде:
Комплексное
число можно представить в виде
Перемножим эти выражения
(1)Слайд 8Значит в использованном выражении (1), интегральная сумма может быть записана
в виде:
(2)
Перейдем к пределу в выражении (2), получим:
Слайд 9Так как f(z) непрерывна на L, то непрерывны в любой
точке u и v (т.к задание f(z) равносильно заданию u
и v)В правой части (3) – интегральные суммы для криволинейных интегралов 2 рода
Из непрерывности u и v следует, что существуют криволинейные интегралы 2 рода как предел своих интегральных сумм.
Слайд 10Так как каждый из пределов входящий, входящий в правую часть
(3) существует и равен соответствующему криволинейному интегралу, то существует и
предел левой части (3) и можем записать(4)
(4) может использоваться и для вычисления интегралов от ФКП.
Слайд 11Свойства интегралов от ФКП.
Если L+ и L- две дуги,
различающиеся только ориентацией, то:
2)
3)
4)
М – действительное число
l –
длина дуги LСлайд 12§ 11.2. Понятие первообразной. Формула Ньютона-Лейбница. Интегрирование по частям и
заменой переменной.
Пусть функция f(z) задана в некоторой односвязной
области D на комплексной плоскости.Если существует функция F(z) в области D, такая что F(z) = f(z), то F(z) называется первообразной для функции f(z).
Слайд 13Теорема (о первообразной)
Если функция f(z) дифференцируема в замкнутой, односвязной области
D, то для нее существует первообразная F(z), определенная на D,
которая задается формулой:Замечание 1: В отличии от функции действительного переменного функцию комплексного переменного необходимо дифференцировать в замкнутой односвязной области для существования первообразной.
Слайд 14Замечание 2: Если f(z) непрерывна в односвязной области D, и
интеграл по любому замкнутому контуру, лежащему в этой области =0,
то в этом случае первообразная так же существует.Замечание 3: Две первообразные ФКП отличаются на константу.
Слайд 15Теорема (Ньютона- Лейбница).
Если f(z) дифференцируема в односвязной области D и
z1, z0 произвольные точки D, а F(z) какая либо первообразная
для f(z), тоТеорема (интегрирование по частям)
Если f(z) и (z) дифференцируемы в односвязной области D, z1, z0 – точки, принадлежащие D, то
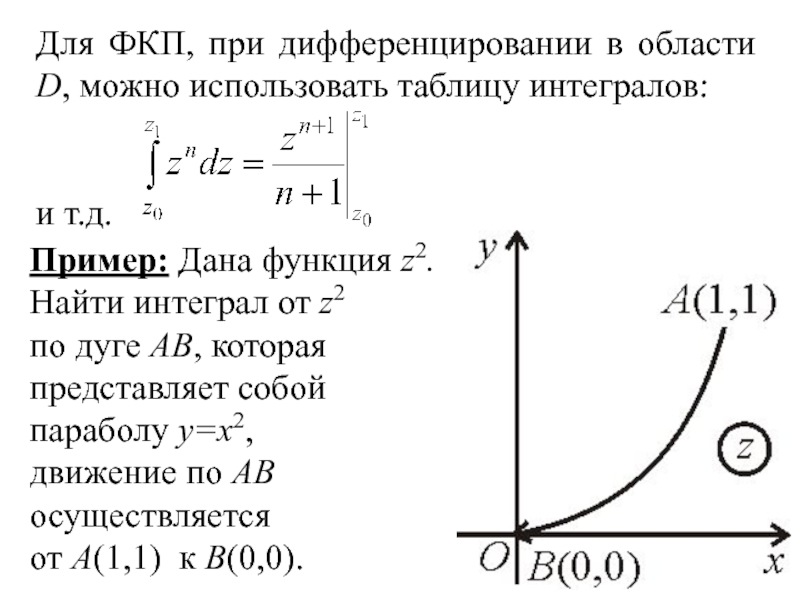
Слайд 16Пример: Дана функция z2.
Найти интеграл от z2
по дуге AB, которая
представляет
собой
параболу y=x2,
движение по AB
осуществляется
от A(1,1) к B(0,0).
Для ФКП, при
дифференцировании в области D, можно использовать таблицу интегралов:и т.д.
Слайд 19§ 11.3 Интегральная теорема Коши
Если функция f(z) аналитична в односвязной
замкнутой области D, то интеграл от этой функции по любому
замкнутому контуру, лежащему в этой области = 0, то есть:L - произвольный контур.
Доказательство.
Так как f(z) аналитична в области D, значит она дифференцируема в односвязной области D; из дифференцируемости следует существование интеграла в области D по любой кривой.
Слайд 20Из аналитичности следует выполнение условий Коши-Римана
Пусть L - произвольный, ориентированный
замкнутый контур, в области D, тогда
(1)формула Грина
Из аналитичности f(z) следует дифференцируемость в области. Применим к криволинейному интегралу 2-го рода, стоящему в правой части (1) формулу Грина:
Слайд 21
0
0D* - область, лежащая внутри L
Из условий Коши-Римана имеем, что подынтегральное выражение = 0.
Значит интеграл от аналитической односвязной функции = 0 по любому замкнутому контуру.
Если область D не является односвязной теорему в этой формулировки применить нельзя