TheSlide.ru

Операции над графами

Содержание

1. Операции над графами
2. План1. Бинарные операции.2. Унарные операции.
3. ПОВТОРЕНИЕГеометрическое представление графа — это схемы, состоящие
4. СПОСОБЫ ОПИСАНИЯ ГРАФОВСпособы описания графовПеречисление элементовИзображениеМатрица смежностиМатрица инциденцийСписки смежности
5. ОПЕРАЦИИ НАД ГРАФАМИИсходные графыРазличают бинарные и унарные операции
6. ОБЪЕДИНЕНИЕ ГРАФОВОбъединением (суммой) множеств А и В
7. ОБЪЕДИНЕНИЕ ГРАФОВПри объединении графов матрица смежности результата
8. ПЕРЕСЕЧЕНИЕ ГРАФОВПересечением (произведением) множеств А и В
9. ПЕРЕСЕЧЕНИЕ ГРАФОВрезультирующая матрица смежности получается операцией поэлементного
10. КОЛЬЦЕВАЯ СУММА ГРАФОВКольцевой суммой множеств А и
11. КОЛЬЦЕВАЯ СУММА ГРАФОВрезультирующая матрица смежности получается операцией поэлементного логического сложения матриц смежности исходных графов
12. УДАЛЕНИЕ ВЕРШИНЫРезультат - граф, получившимся после удаления
13. УДАЛЕНИЕ РЕБРА ИЛИ ДУГИКонцевые вершины удаляемого ребра
14. ЗАМЫКАНИЕ (ОТОЖДЕСТВЛЕНИЕ)пара вершин хi и xj в
15. СТЯГИВАНИЕвверху – стягивание дуги a1, внизу –
16. Контрольные вопросыВыполнить операцию пересечения для графов, показанных на рисунке.
17. Контрольные вопросыВыполнить операцию пересечения для графов, представленных матрицами смежности смежности.
18. Слайд 18
19. Слайд 19
20. Слайд 20
21. Слайд 21
22. Слайд 22
23. Слайд 23
24. Слайд 24
25. Источники информацииПрограммирование, компьютеры и сети https://progr-system.ru/
26. Благодарю за внимание!
27. Скачать презентанцию

План1. Бинарные операции.2. Унарные операции.

Слайды и текст этой презентации

Слайд 1Операции над графами
Преподаватель: Солодухин Андрей Геннадьевич

Операции над графамиПреподаватель: Солодухин Андрей Геннадьевич

Слайд 2План
1. Бинарные операции.
2. Унарные операции.

План1. Бинарные операции.2. Унарные операции.

Слайд 3ПОВТОРЕНИЕ
Геометрическое представление графа — это схемы, состоящие из точек и

соединяющих эти точки отрезков прямых или кривых
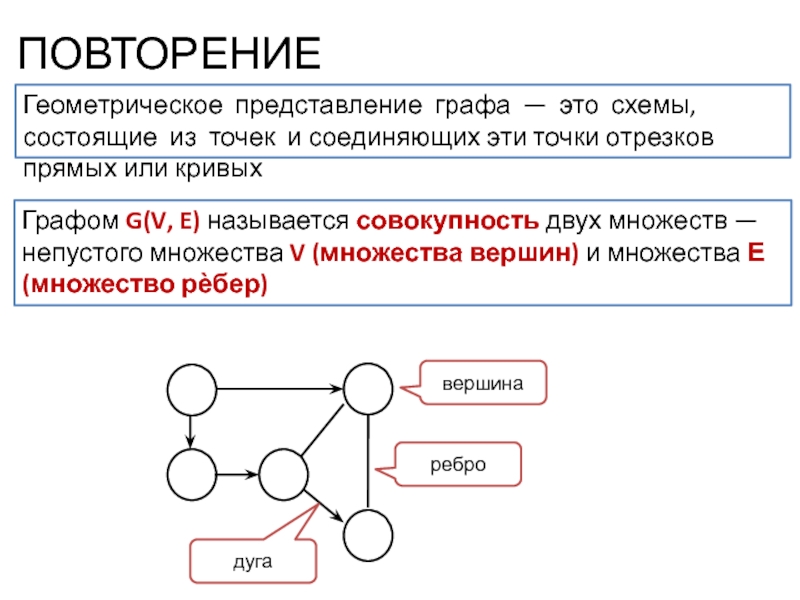
Графом G(V, E) называется

совокупность двух множеств — непустого множества V (множества вершин) и множества E (множество рѐбер)

вершина

ребро

дуга

ПОВТОРЕНИЕГеометрическое представление графа — это схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривыхГрафом

Слайд 4СПОСОБЫ ОПИСАНИЯ ГРАФОВ
Способы описания графов
Перечисление элементов
Изображение
Матрица смежности
Матрица инциденций
Списки смежности

СПОСОБЫ ОПИСАНИЯ ГРАФОВСпособы описания графовПеречисление элементовИзображениеМатрица смежностиМатрица инциденцийСписки смежности

Слайд 5ОПЕРАЦИИ НАД ГРАФАМИ
Исходные графы
Различают бинарные и унарные операции

ОПЕРАЦИИ НАД ГРАФАМИИсходные графыРазличают бинарные и унарные операции

Слайд 6ОБЪЕДИНЕНИЕ ГРАФОВ
Объединением (суммой) множеств А и В называется множество А

∪ В, элементы которого принадлежат хотя бы одному из этих

множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

ОБЪЕДИНЕНИЕ ГРАФОВОбъединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы

Слайд 7ОБЪЕДИНЕНИЕ ГРАФОВ
При объединении графов матрица смежности результата получается операцией поэлементного

логического сложения матриц смежности исходных графов G1 и G2 .

ОБЪЕДИНЕНИЕ ГРАФОВПри объединении графов матрица смежности результата получается операцией поэлементного логического сложения матриц смежности исходных графов G1

Слайд 8ПЕРЕСЕЧЕНИЕ ГРАФОВ
Пересечением (произведением) множеств А и В называется множество А

∩ В, элементы которого принадлежат как множеству А, так и

множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

ПЕРЕСЕЧЕНИЕ ГРАФОВПересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству

Слайд 9ПЕРЕСЕЧЕНИЕ ГРАФОВ
результирующая матрица смежности получается операцией поэлементного логического умножения матриц

смежности исходных графов G1 и G2

ПЕРЕСЕЧЕНИЕ ГРАФОВрезультирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G1 и G2

Слайд 10КОЛЬЦЕВАЯ СУММА ГРАФОВ
Кольцевой суммой множеств А и В называют множество,

состоящее из тех и только тех элементов, которые принадлежат множеству

А, но не принадлежат множеству В или принадлежат множеству В, но не принадлежат множеству А.

КОЛЬЦЕВАЯ СУММА ГРАФОВКольцевой суммой множеств А и В называют множество, состоящее из тех и только тех элементов,

Слайд 11КОЛЬЦЕВАЯ СУММА ГРАФОВ
результирующая матрица смежности получается операцией поэлементного логического сложения

матриц
смежности исходных графов

КОЛЬЦЕВАЯ СУММА ГРАФОВрезультирующая матрица смежности получается операцией поэлементного логического сложения матриц смежности исходных графов

Слайд 12УДАЛЕНИЕ ВЕРШИНЫ
Результат - граф, получившимся после удаления из графа G

вершины хi и всех ребер, инцидентных этой вершине
Удалена вершина x3,

в матрице смежности удалены строка 3 и столбец 3

УДАЛЕНИЕ ВЕРШИНЫРезультат - граф, получившимся после удаления из графа G вершины хi и всех ребер, инцидентных этой

Слайд 13УДАЛЕНИЕ РЕБРА ИЛИ ДУГИ
Концевые вершины удаляемого ребра НЕ УДАЛЯЮТСЯ
Удалены дуги

a4 и a7, в матрице смежности элементы A23, A43

УДАЛЕНИЕ РЕБРА ИЛИ ДУГИКонцевые вершины удаляемого ребра НЕ УДАЛЯЮТСЯУдалены дуги a4 и a7, в матрице смежности элементы

Слайд 14ЗАМЫКАНИЕ (ОТОЖДЕСТВЛЕНИЕ)
пара вершин хi и xj в графе G замыкается

(или отождествляется), если они заменяются такой новой вершиной, что все

дуги в графе G, инцидентные хi и xj , становятся инцидентными новой вершине

Замкнуты вершины x1 и x2. Матрица смежности графа после выполнения операции замыкания вершин хi и xj получается путем поэлементного логического сложения i-го и j-го столбцов и i-ой и j-ой строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали

ЗАМЫКАНИЕ (ОТОЖДЕСТВЛЕНИЕ)пара вершин хi и xj в графе G замыкается (или отождествляется), если они заменяются такой новой

Слайд 15СТЯГИВАНИЕ
вверху – стягивание дуги a1, внизу – дуг a1 ,

a6 и a7
Под стягиванием подразумевают операцию удаления дуги или ребра

и отождествление его концевых вершин

СТЯГИВАНИЕвверху – стягивание дуги a1, внизу – дуг a1 , a6 и a7Под стягиванием подразумевают операцию удаления

Слайд 16Контрольные вопросы
Выполнить операцию пересечения для графов, показанных на рисунке.

Контрольные вопросыВыполнить операцию пересечения для графов, показанных на рисунке.

Слайд 17Контрольные вопросы
Выполнить операцию пересечения для графов, представленных матрицами смежности смежности.

Контрольные вопросыВыполнить операцию пересечения для графов, представленных матрицами смежности смежности.

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25Источники информации
Программирование, компьютеры и сети https://progr-system.ru/

Источники информацииПрограммирование, компьютеры и сети https://progr-system.ru/

Слайд 26Благодарю за внимание!

Благодарю за внимание!

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей