Описание и преобразование управляющих процессов

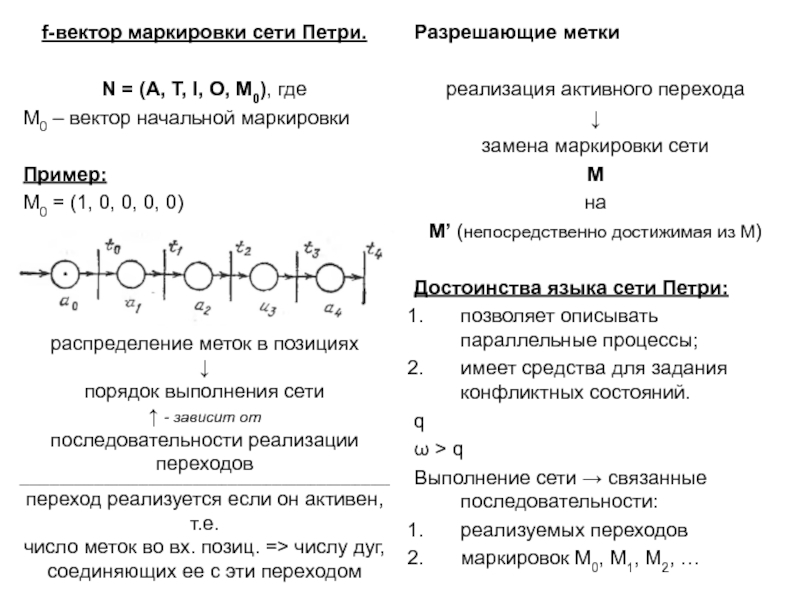
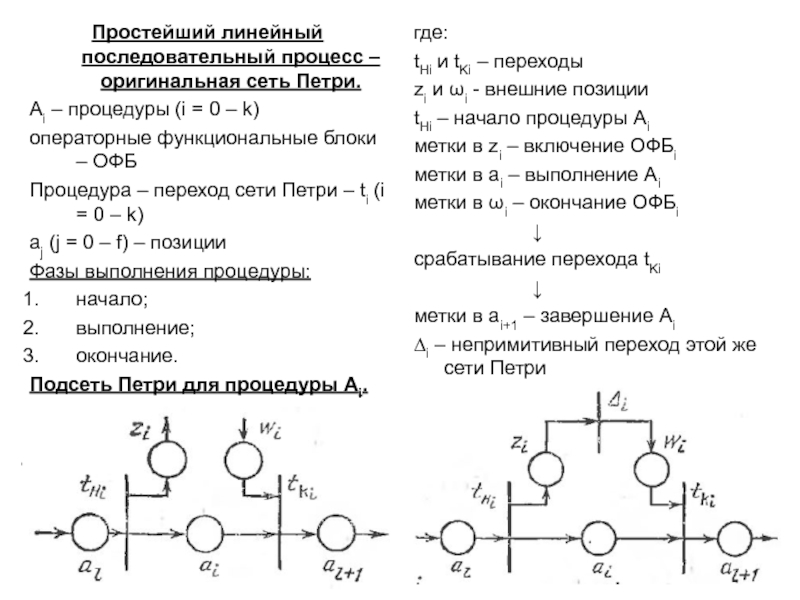
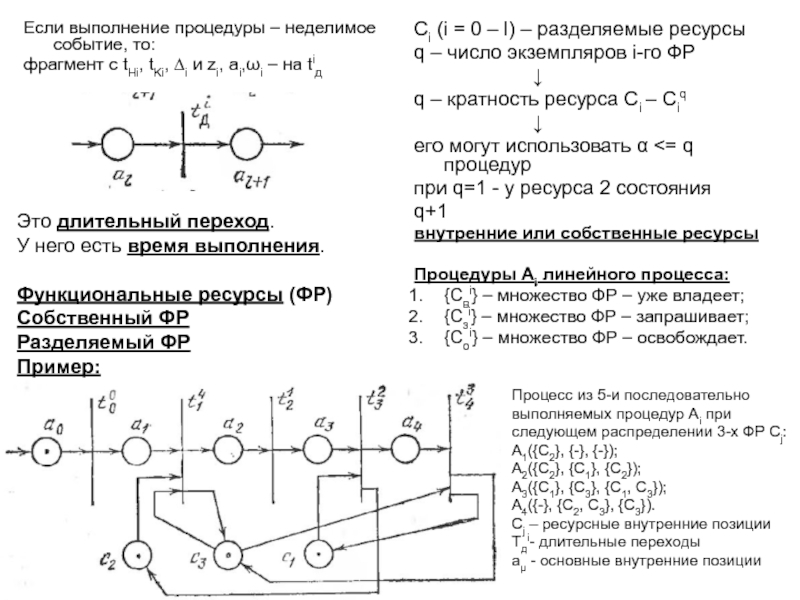
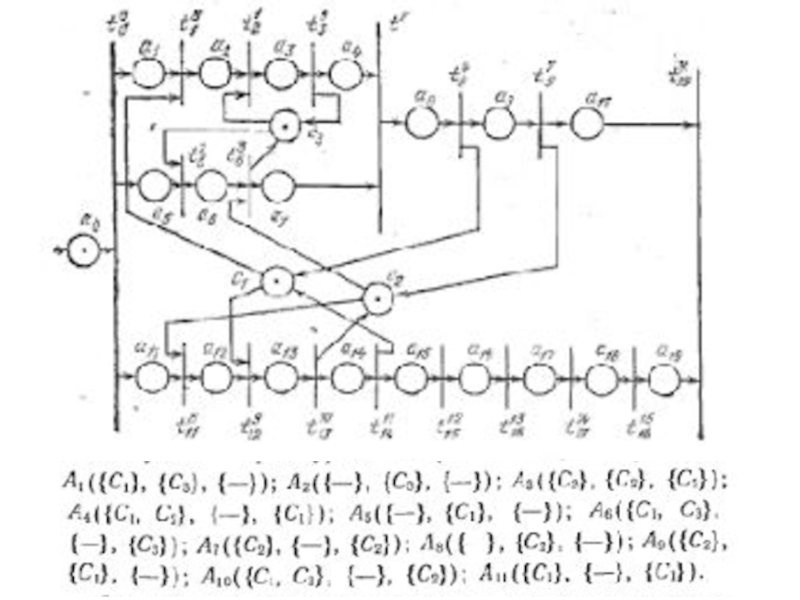
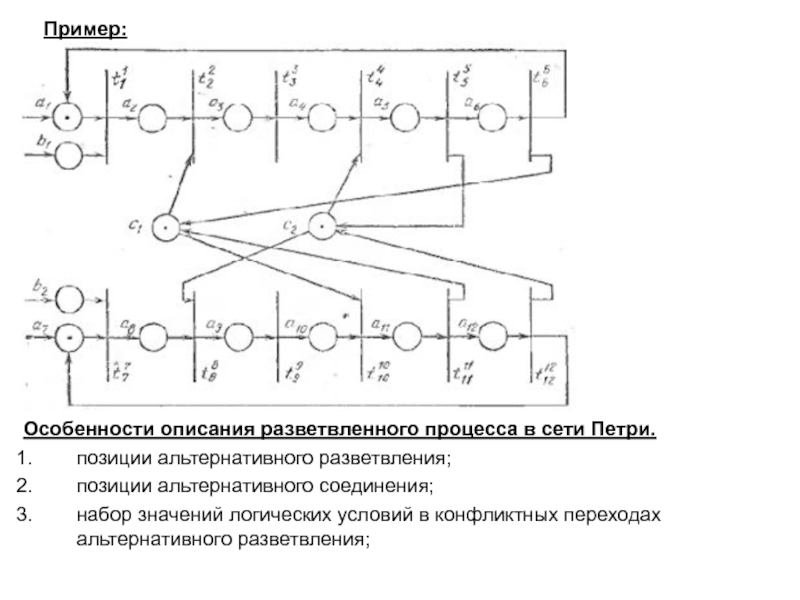
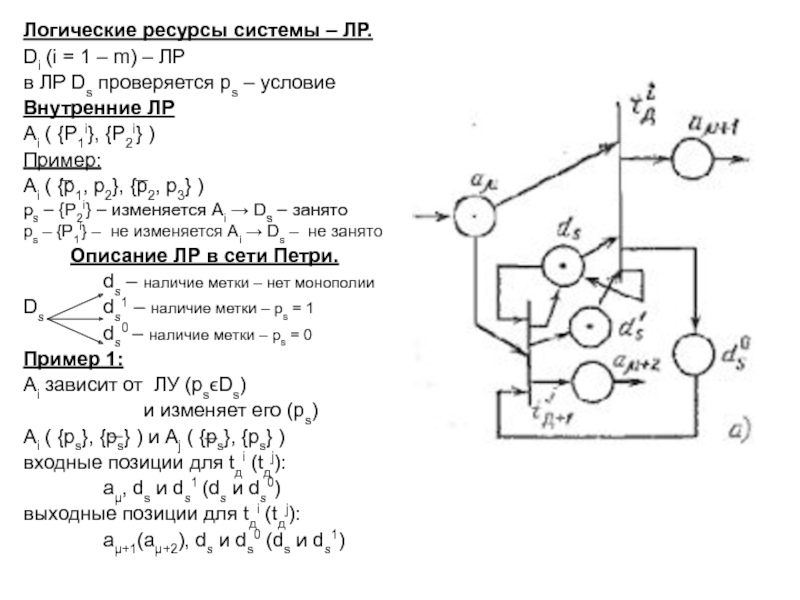
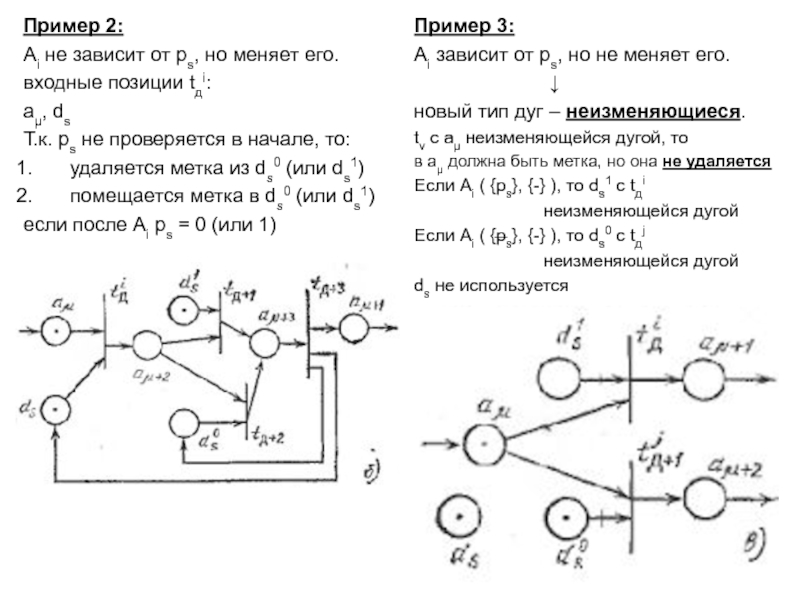
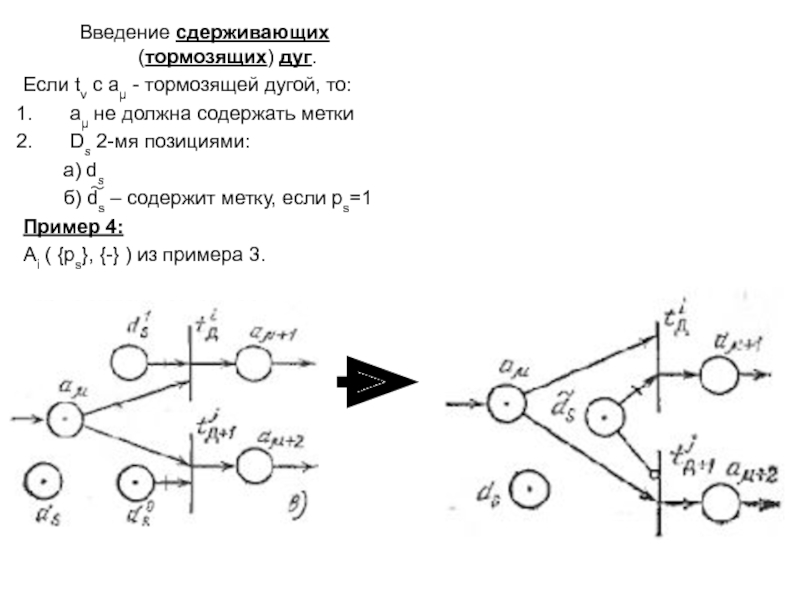
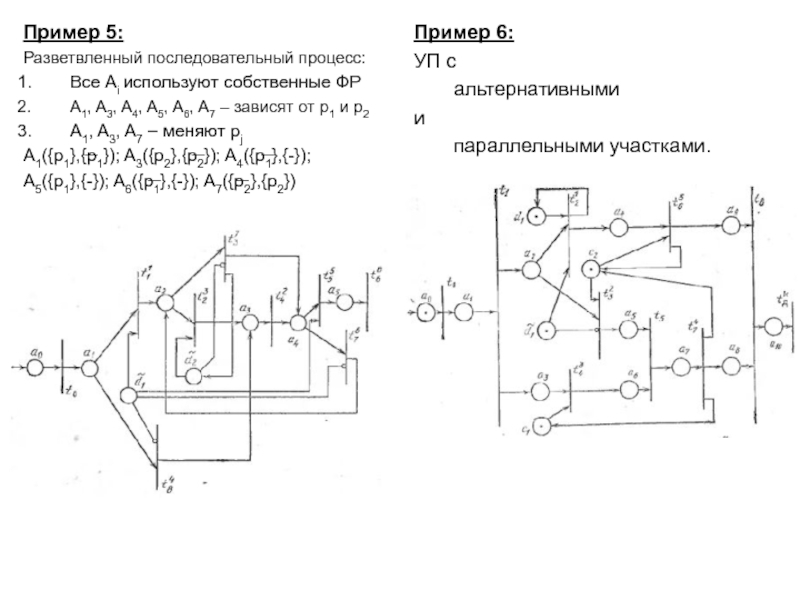
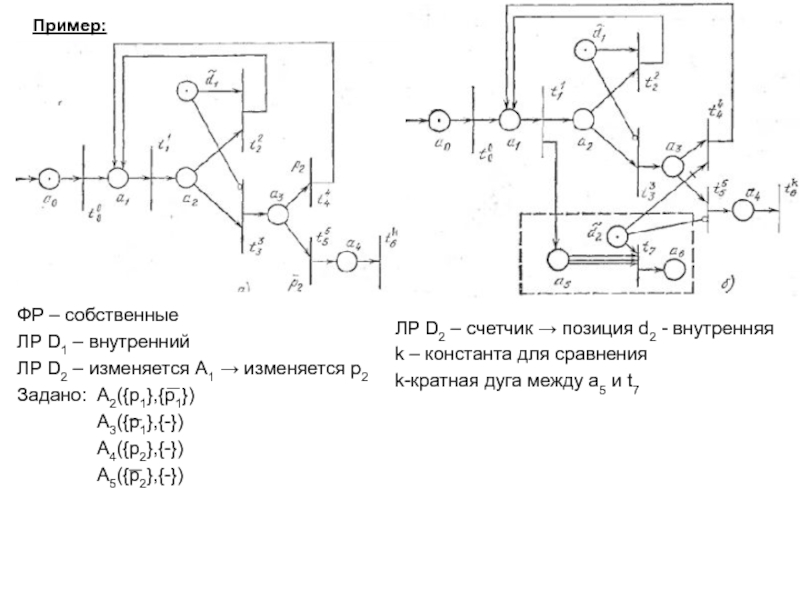
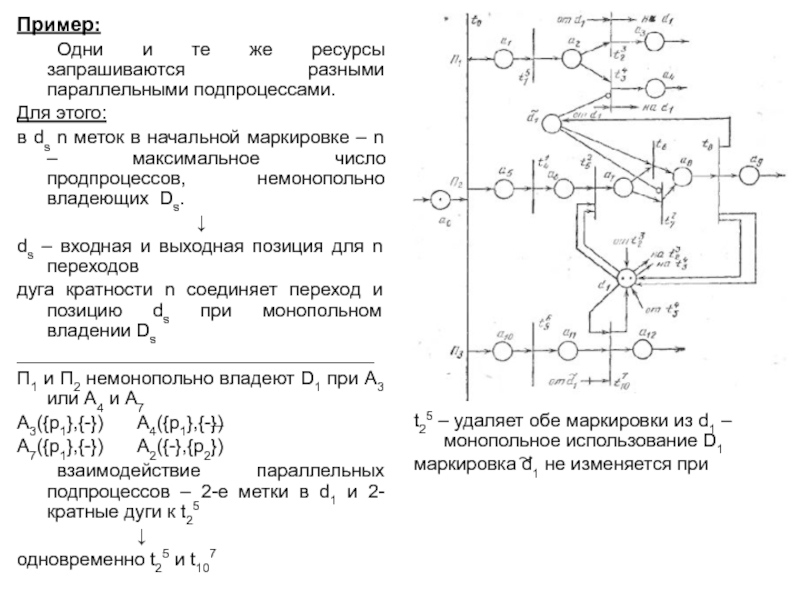
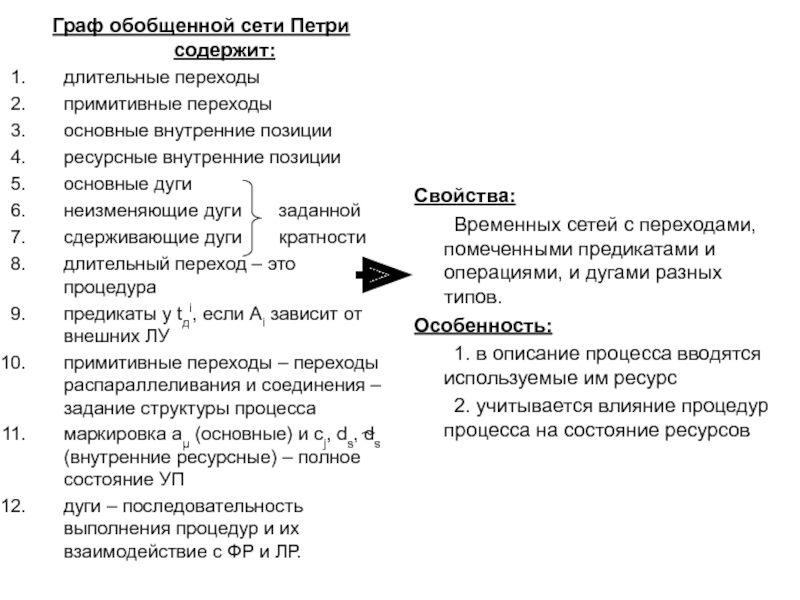
понятия – базис сетей Петри:
событие;
условие.

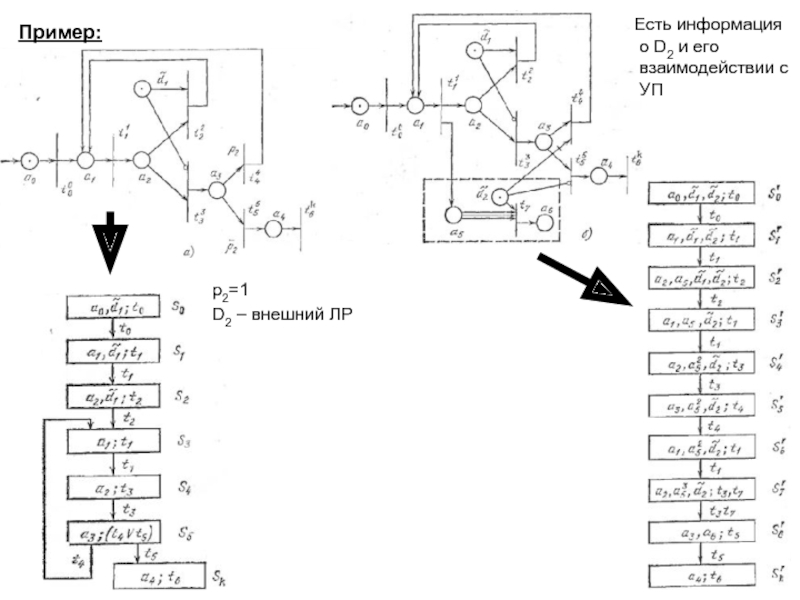
Сеть Петри – структура УП
↓
это последовательность
процедур

Условия

→ событие
Состояние системы – это множество условий

Событие → новые условия →
→ изменение состояния системы

События – множество переходов
T={t0, t1, …, tr}
Условия – множество позиций
A={a0, a1, …, af}
I – входная функция
связь T и A
O – выходная функция
I – отображает tv(v=0 r) в мн-во позиций I(tv) – входные позиции перехода
O – отображает tv в мн-во позиций O(tv) – выходные позиции перехода
aµ - входная позиция tv, если aµ ϵ I(tv)
aµ - выходная позиция tv, если aµϵO(tv)

Сеть Петри – N = (A, T, I, O)

t2, t3, t4}
I(t0) = a0 I(t1) = a1
I(t2) = a2

I(t3) = a3
I(t4) = a4
O(t0) = a1 O(t1) = a2
O(t2) = a3 O(t3) = a4

I – матрица следования
O – матрица предшествования

Графическое представление
сети Петри

Типы вершин:
позиции – «O»
переходы – «|»

if (aµ - вход для tv), then (дуга aµ→ tv)
if (aµ - выход для tv), then (дуга tv→ aµ)
↓
G = (V, W) – ориентированный двудольный мультиграф, где
V – множество вершин
W – множество направленных дуг
V = A U T A ∩ T = Ø

позиция – условие
↓
Выполнение условия – маркировка позиции
(метка – «точка» в позиции)
↓
ʘ
↓
Если несколько точек –
то «емкость условия»

где
M0 – вектор начальной маркировки

Пример:
M0 = (1, 0, 0, 0,

0)

Разрешающие метки

реализация активного перехода
↓
замена маркировки сети
M
на
M’ (непосредственно достижимая из M)

Достоинства языка сети Петри:
позволяет описывать параллельные процессы;
имеет средства для задания конфликтных состояний.
q
ω > q
Выполнение сети → связанные последовательности:
реализуемых переходов
маркировок M0, M1, M2, …

распределение меток в позициях
↓
порядок выполнения сети
↑ - зависит от
последовательности реализации
переходов
___________________________________________________________________________
переход реализуется если он активен,
т.е.
число меток во вх. позиц. => числу дуг,
соединяющих ее с эти переходом

маркировки может содержать лишь 0 и 1;
реализация активного перехода возможна,

если ни 1 из его выходных позиций не содержит меток – число меток в любой позиции не больше 1;
конечное число состояний – 2f при f позициях.

Ограниченная сеть Петри.

k → k-безопасная позиция или k-ограниченная
k’ >= k – k’-безопасной
kmax

Ограничение оригинальной сети Петри – моделирование примитивных событий.
________________________________
это сеть позиция-переход
↓
автоматная сеть
↓
маркированный граф
________________________________
сети с предикатами на переходах
↓
расширение ее описательных возможностей
________________________________
Введение позиции времени в сети Петри.
Временные сети: переход – t;
Тайм-аутные сети: переход – a и b.

цветов

Численные сети Петри.
метки любой природы и величины;
условия активизация и результата

реализации независимы;
при реализации переходов изменяется маркировка входных и выходных позиций и содержимое памяти данных

Использование дуг разных типов в сети Петри.
Существуют:
Простые дуги:
1.1. активизирующая;
1.2. сдерживающая;
1.3. входная;
1.4. выходная;
Составные дуги:
2.1. активизирующая входная;
2.2. сдерживающая выходная.

(i = 0 – k)
операторные функциональные блоки – ОФБ
Процедура –

переход сети Петри – ti (i = 0 – k)
aj (j = 0 – f) – позиции
Фазы выполнения процедуры:
начало;
выполнение;
окончание.
Подсеть Петри для процедуры Ai.

где:
tHi и tKi – переходы
zi и ωi - внешние позиции
tHi – начало процедуры Ai
метки в zi – включение ОФБi
метки в ai – выполнение Ai
метки в ωi – окончание ОФБi
↓
срабатывание перехода tKi
↓
метки в ai+1 – завершение Ai
∆i – непримитивный переход этой же сети Петри

∆i и zi, ai,ωi – на tiд
Ci (i = 0

– l) – разделяемые ресурсы
q – число экземпляров i-го ФР
↓
q – кратность ресурса Ci – Ciq
↓
его могут использовать α <= q процедур
при q=1 - у ресурса 2 состояния
q+1
внутренние или собственные ресурсы

Процедуры Ai линейного процесса:
{Cвi} – множество ФР – уже владеет;
{Cзi} – множество ФР – запрашивает;
{Cоi} – множество ФР – освобождает.

Это длительный переход.
У него есть время выполнения.

Функциональные ресурсы (ФР)
Собственный ФР
Разделяемый ФР
Пример:

Процесс из 5-и последовательно
выполняемых процедур Ai при
следующем распределении 3-х ФР Cj:
A1({C2}, {-}, {-});
A2({C2}, {C1}, {C2});
A3({C1}, {C3}, {C1, C3});
A4({-}, {C2, C3}, {C3}).
Сj – ресурсные внутренние позиции
Tдi- длительные переходы
aµ - основные внутренние позиции

Ai({C1}, {C3, C4}, {C1, C4})
{Cзi}∩{Cвi}=Ø
Иногда: {Cвi}=Ø и {Cзi}={Cоi}

Особенности описания параллельного

линейного процесса в сети Петри.

длительные переходы – процедуры;
tR – переходы распараллеливания;
tS – переходы соединения;
наличие элементарных подпроцессов;
cобственные ФР подпроцесса

Пример:

соединения;
набор значений логических условий в конфликтных переходах альтернативного разветвления;

– ЛР
в ЛР Ds проверяется ps – условие
Внутренние ЛР
Ai (

{P1i}, {P2i} )
Пример:
Ai ( {p1, p2}, {p2, p3} )
ps – {P2i} – изменяется Ai → Ds – занято
ps – {P1i} – не изменяется Ai → Ds – не занято
Описание ЛР в сети Петри.
ds – наличие метки – нет монополии
Ds ds1 – наличие метки – ps = 1
ds0 – наличие метки – ps = 0
Пример 1:
Ai зависит от ЛУ (psϵDs)
и изменяет его (ps)
Ai ( {ps}, {ps} ) и Aj ( {ps}, {ps} )
входные позиции для tдi (tдj):
aµ, ds и ds1 (ds и ds0)
выходные позиции для tдi (tдj):
aµ+1(aµ+2), ds и ds0 (ds и ds1)

tдi:
aµ, ds
Т.к. ps не проверяется в начале, то:
удаляется метка из

ds0 (или ds1)
помещается метка в ds0 (или ds1)
если после Ai ps = 0 (или 1)

Пример 3:
Ai зависит от ps, но не меняет его.
↓
новый тип дуг – неизменяющиеся.
tv c aµ неизменяющейся дугой, то
в aµ должна быть метка, но она не удаляется
Если Ai ( {ps}, {-} ), то ds1 c tдi
неизменяющейся дугой
Если Ai ( {ps}, {-} ), то ds0 c tдj
неизменяющейся дугой
ds не используется

то:
aµ не должна содержать метки
Ds 2-мя позициями:
а) ds
б) ds –

содержит метку, если ps=1
Пример 4:
Ai ( {ps}, {-} ) из примера 3.

A5, A6, A7 – зависят от p1 и p2
A1, A3,

A7 – меняют pj
A1({p1},{p1}); A3({p2},{p2}); A4({p1},{-});
A5({p1},{-}); A6({p1},{-}); A7({p2},{p2})

Пример 6:
УП с
альтернативными
и
параллельными участками.

hu – метка есть, если pu=1; нет при pu=0
внеш. ЛУ

ϵ {P1}
есть внутренние и внешние ЛУ
если Ai выполняется при pu=1 (0), то hu соединяется с tдi сдерживающей дугой
не включается позиция состояния внешнего ЛР
развитие процесса – зависит от начальной маркировки внутренних позиций и текущей маркировки внешних входных позиций
замена внешних входных позиций на предикаты, зависящие от внешних ЛУ

Если не определено влияние Ai на значение ps:
возможное изменение ps – это безразличное значение (ps) в {P2i}
позиция состояния Ds - в описании параллельного процесса
на время выполнения tдi метка из ds удаляется
позиция ds аналогична внешней позиции

→ изменяется p2
Задано: A2({p1},{p1})
A3({p1},{-})
A4({p2},{-})
A5({p2},{-})
ЛР D2 – счетчик → позиция d2 -

внутренняя
k – константа для сравнения
k-кратная дуга между a5 и t7

ds n меток в начальной маркировке – n – максимальное

число продпроцессов, немонопольно владеющих Ds.
↓
ds – входная и выходная позиция для n переходов
дуга кратности n соединяет переход и позицию ds при монопольном владении Ds
__________________________________
П1 и П2 немонопольно владеют D1 при A3 или A4 и А7
A3({p1},{-}) A4({p1},{-})
A7({p1},{-}) A2({-},{p2})
взаимодействие параллельных подпроцессов – 2-е метки в d1 и 2-кратные дуги к t25
↓
одновременно t25 и t107

t25 – удаляет обе маркировки из d1 – монопольное использование D1
маркировка d1 не изменяется при

позиции
основные дуги
неизменяющие дуги заданной
сдерживающие дуги

кратности
длительный переход – это процедура
предикаты у tдi, если Ai зависит от внешних ЛУ
примитивные переходы – переходы распараллеливания и соединения – задание структуры процесса
маркировка aµ (основные) и cj, ds, ds (внутренние ресурсные) – полное состояние УП
дуги – последовательность выполнения процедур и их взаимодействие с ФР и ЛР.

Свойства:
Временных сетей с переходами, помеченными предикатами и операциями, и дугами разных типов.
Особенность:
1. в описание процесса вводятся используемые им ресурс
2. учитывается влияние процедур процесса на состояние ресурсов

достижимых состояний сетей Петри.
М0 tl М1

ω – бесконечное число меток

Неограниченные и ограниченные

сети Петри.

Описание графа достижимых маркировок:
GN
Mi
aµ
Si

Влияние структуры процесса на наличие тупиковых состояний.
Пример:

Предположение – время
реализации всех перехо-
дов одинаково.

tдк при p=1 в S4 - тупик

– вместо t2 будет активизирован t3.

левая ветвь – p=1
правая ветвь

– p=0

S4 и S7 – тупиковые

Реализация активизированных переходов завершается одновременно.

Это граф статических состояний процесса.

дуги – переходы, закончившие реализацию.

В скобках – переходы, продолжающие реализацию.

↓
Неустойчивые состояния.

S8 a3 a6 t4
S4 и S7 – тупиковые

Причина – недопустимая структура процесса.

Граф, содержащий статические и промежуточные состояния.

циклы.

Пример:
Для фиксированной начальной позиции d1 и d2.
Полный граф достижимости

и его взаимодействии с УП

циклические процессы
С1 и С2 – разделяемые ФР
b1 и b2 –

внешние входные позиции

П1 – по горизонтали
П2 – по вертикали
Sij – вершины, состояния, где i – номер в П1, а j – в П2

Sб:
aµ ti
Состояние взаимной блокировки – Sв.б
Состояние полной взаимной блокировки – Sп.в.б
Тупиковое

состояние – Sт –
это Sв.б и Sп.в.б
Предтупиковое состояние – Sп.т
Qз{Sт, Sп.т} – множество запрещенных состояний
Опасное состояние - Sоп, если:
Sv ребро Su
и
SvϵQз, а SuϵQз
Qоп – множество опасных состояний
Безопасное состояние

Состояние конфликта – Sкн

Опасные отрезки пути в графе

Корень опасных отрезков – Sк.оп

Дополнительная блокирующая позиция – аб