Определение графа

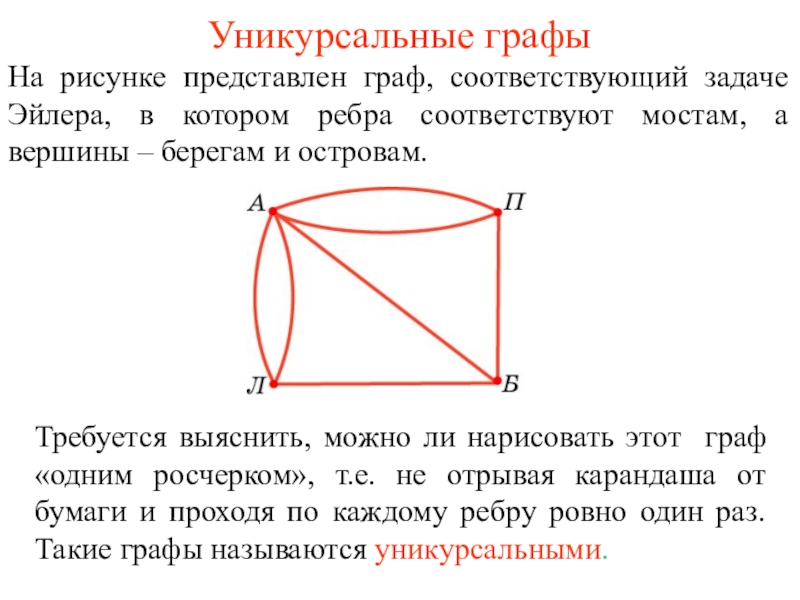
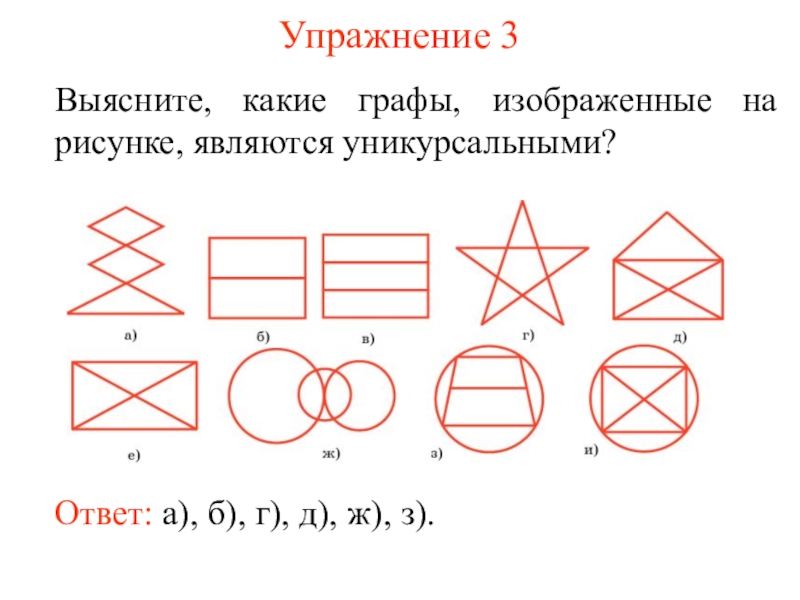
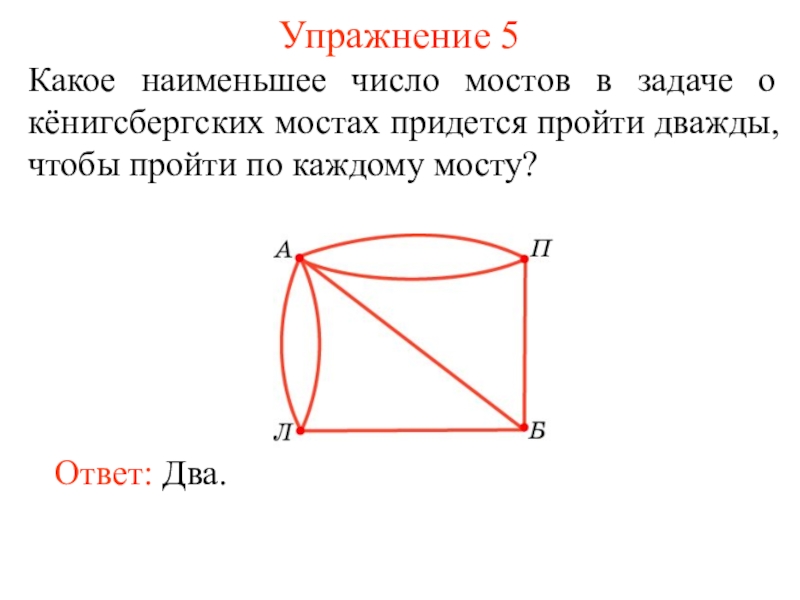
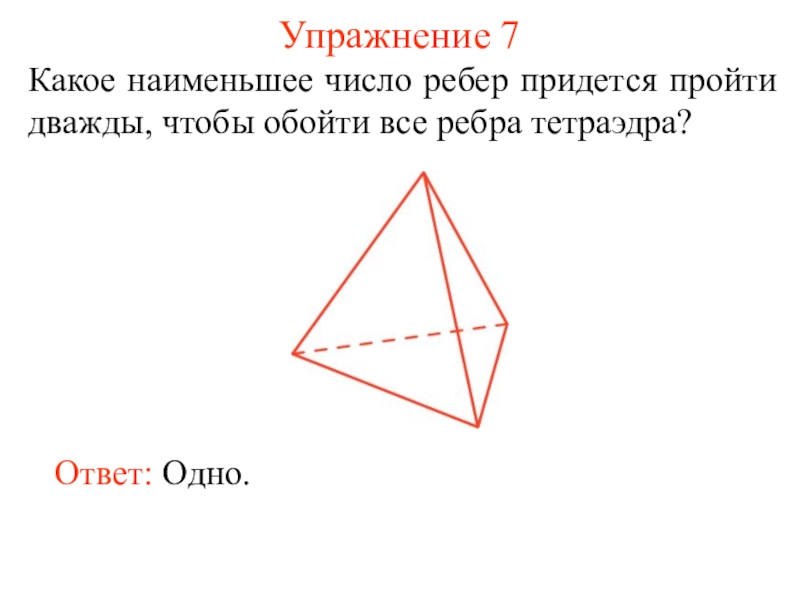
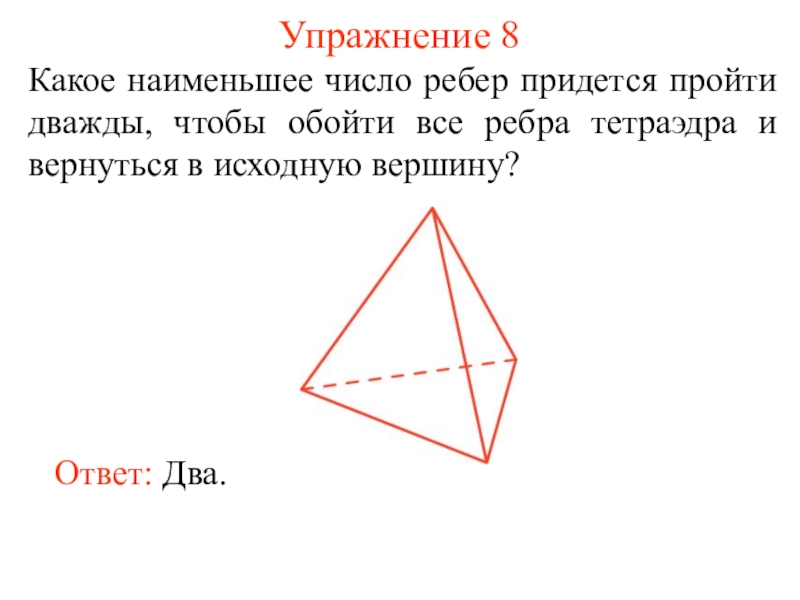
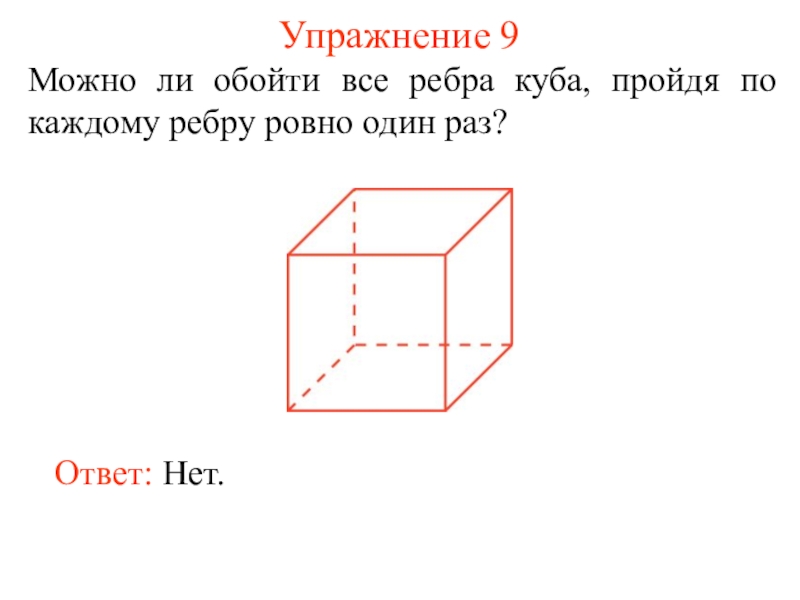
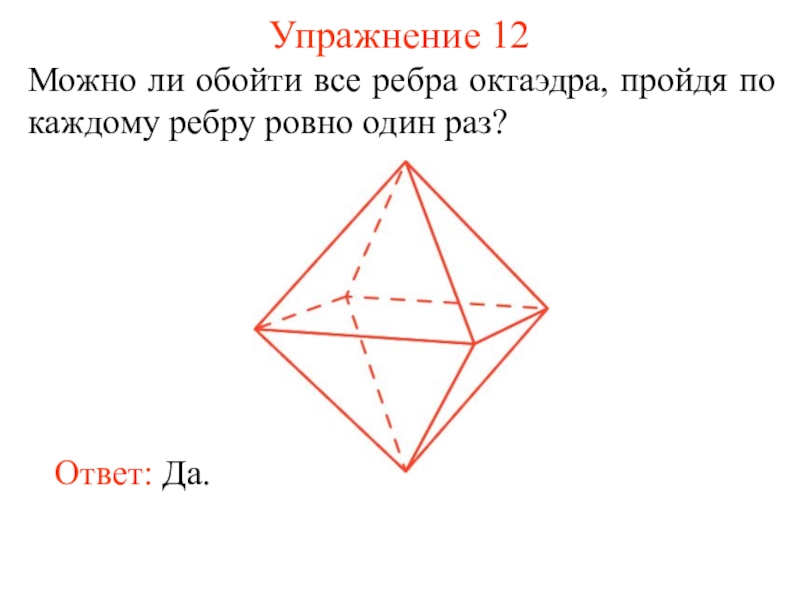
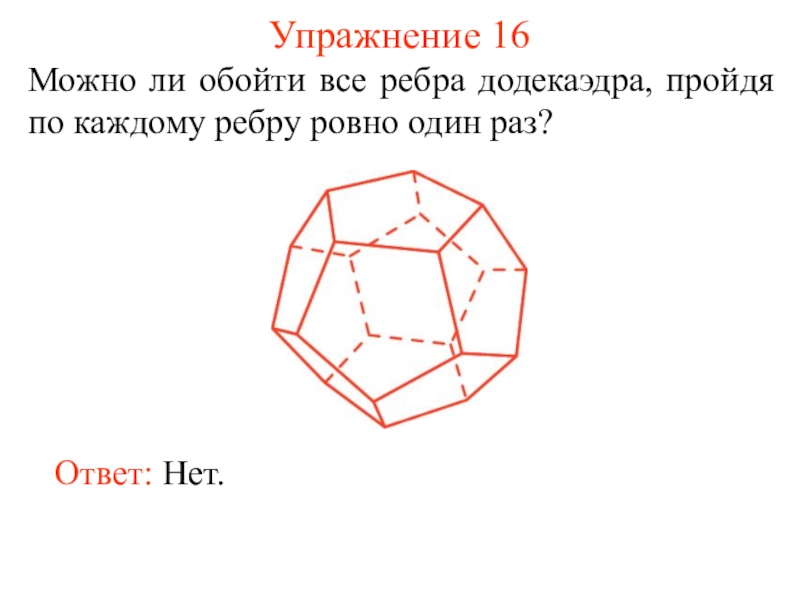
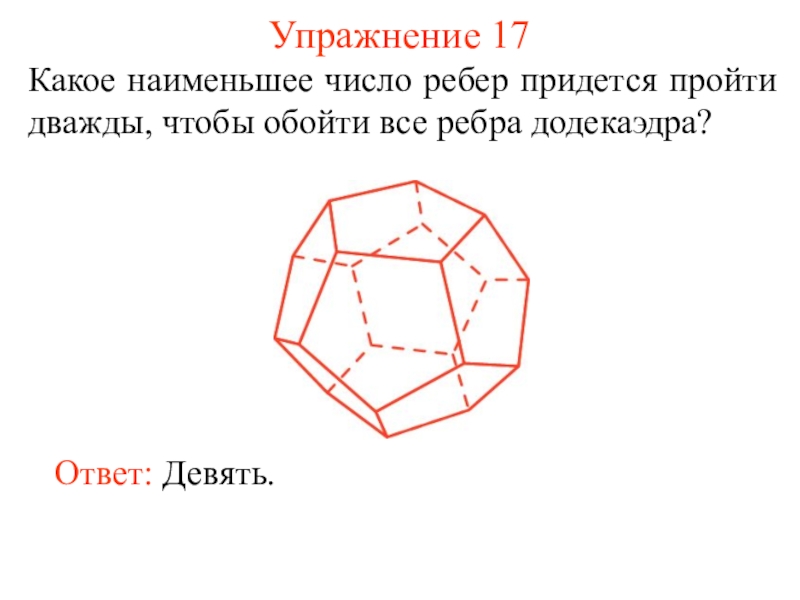
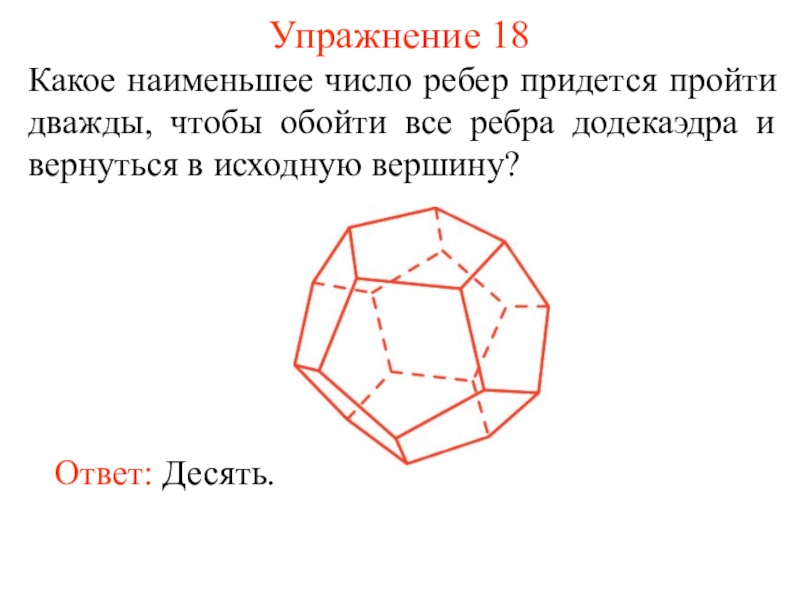
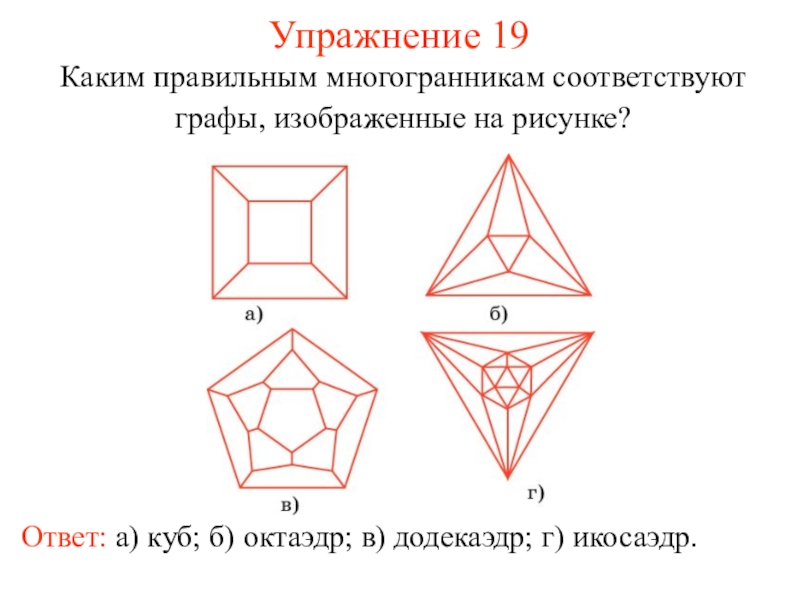
некоторые из этих точек, называется плоским графом, или просто графом.

Точки называются вершинами, а отрезки – ребрами графа.
Граф называется связным, если любые две его вершины можно соединить ломаной, состоящей из ребер графа.
Граф называется простым, если его ребра не пересекаются, т.е. не имеют общих внутренних точек.
Вместо отрезков в качестве ребер графов рассматриваются также кривые линии.

лишним лет назад. Одной из таких задач-головоломок была задача о

кенигсбергских мостах, которая привлекла к себе внимание Леонарда Эйлера (1707-1783), долгое время жившего и работавшего в России (с 1727 по 1741 год и с 1766 до конца жизни).

Задача. В г. Кёнигсберге (ныне Калининград) было семь мостов через реку Прегель (Л - левый берег, П - правый берег, А и Б - острова). Можно ли, прогуливаясь вдоль реки, пройти по каждому мосту ровно один раз?

ребра соответствуют мостам, а вершины – берегам и островам.
Требуется

выяснить, можно ли нарисовать этот граф «одним росчерком», т.е. не отрывая карандаша от бумаги и проходя по каждому ребру ровно один раз. Такие графы называются уникурсальными.

вершине (ребра, с началом и концом в данной вершине считаются

дважды).

Теорема. Для уникурсального графа число вершин нечетного индекса равно нулю или двум.

Доказательство. Если граф уникурсален, то у него есть начало и конец обхода. Остальные вершины имеют четный индекс, так как с каждым входом в такую вершину есть и выход. Если начало и конец не совпадают, то они являются единственными вершинами нечетного индекса. У начала выходов на один больше, чем входов, а у конца входов на один больше, чем выходов. Если начало совпадает с концом, то вершин с нечетным индексом нет.

Верно и обратное: Если у связного графа число вершин нечетного индекса равно нулю или двум, то он является уникурсальным.

Эйлера. Вершина А имеет индекс 5, Б - 3, П

- 3 и Л - 3. Таким образом, мы имеем четыре вершины нечетного индекса, и, следовательно, данный граф не является уникурсальным. Значит, нельзя пройти по каждому из семи мостов только один раз.

конечным набором точек плоскости и отрезков, соединяющих некоторые из этих

точек.

его можно ли нарисовать «одним росчерком», т.е. не отрывая карандаша

от бумаги и проходя по каждому ребру ровно один раз.

называется число ребер, сходящихся в этой вершине (ребра, с началом

и концом в данной вершине считаются дважды).

уникурсального графа число вершин нечетного индекса равно нулю или двум.

3. Сколько у него ребер? Нарисуйте такой граф.

4. Сколько у него ребер? Нарисуйте такой граф.

б), г), д), ж), з).

б) две вершины нечетного индекса; в) три вершины нечетного индекса;

г) четыре вершины нечетного индекса?

Ответ: а), в) Нет; б), г) да.

придется пройти дважды, чтобы пройти по каждому мосту?
Ответ: Два.

ребру ровно один раз?
Ответ: Нет.

все ребра тетраэдра?
Ответ: Одно.

все ребра тетраэдра и вернуться в исходную вершину?
Ответ: Два.

ребру ровно один раз?
Ответ: Нет.

все ребра куба?
Ответ: Три.

все ребра куба и вернуться в исходную вершину?
Ответ: Четыре.

ребру ровно один раз?
Ответ: Да.

ребру ровно один раз?
Ответ: Нет.

все ребра икосаэдра?
Ответ: Пять.

все ребра икосаэдра и вернуться в исходную вершину?
Ответ: Шесть.

ребру ровно один раз?
Ответ: Нет.

все ребра додекаэдра?
Ответ: Девять.

все ребра додекаэдра и вернуться в исходную вершину?
Ответ: Десять.

а) куб; б) октаэдр; в) додекаэдр; г) икосаэдр.