Определенный интеграл. Формула Ньютона- Лейбница. Приложения определенного интеграла

Содержание

1. Определенный интеграл. Формула Ньютона- Лейбница. Приложения определенного интеграла
2. ПЛАНПонятие определенного интеграла.Свойства определенного интеграла.Метод замены переменной.Несобственные интегралы.Приложения определенного интеграла.
3. 1. Понятие определенного интегралаК понятию определенного интеграла
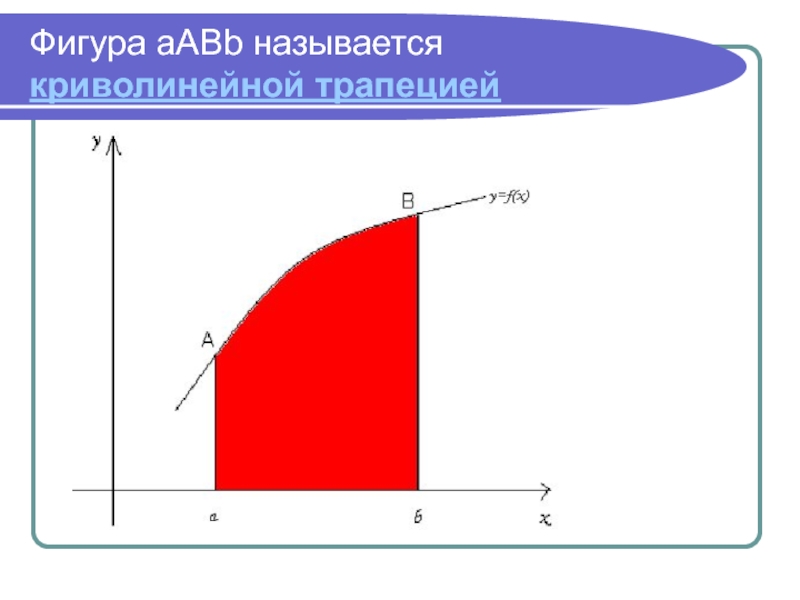
4. Фигура aABb называется криволинейной трапецией
5. Def.Под определенным интегралом
6. Правило:Определенный интеграл равен разности значений первообразной подынтегральной
7. Готфрид Вильгельм Лейбниц(1646 – 1716 гг.) Выдающийся немецкий
8. Исаак НЬЮТОН (Newton) (04.01.1643 - 31.03.1727) Английский физик и
9. 2. Основные свойства определенного интеграла.1)Величина определенного интеграла
10. 3) При перестановке пределов интегрирования определенный интеграл меняет
11. 5)Постоянный множитель можно выносить за знак определенного
12. 3. Замена переменной в определенном интеграле. где для
13. 4. Несобственные интегралы.Def: Пусть функция f(x) определена на
14. Таким образом, по определению, Если этот предел -
15. ПУАССОН, СИМЕОН ДЕНИ (Poisson, Simeon-Denis) (1781–1840 гг.) Французский
16. Интеграл Пуассона:если а = 1, тоИнтеграл сходится, и его значение .
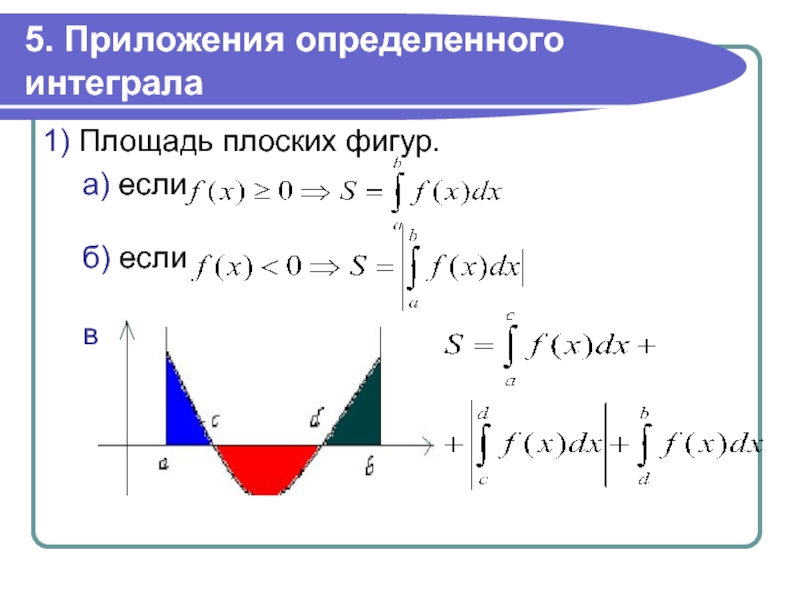
17. 5. Приложения определенного интеграла1) Площадь плоских фигур. а) если б) если в)
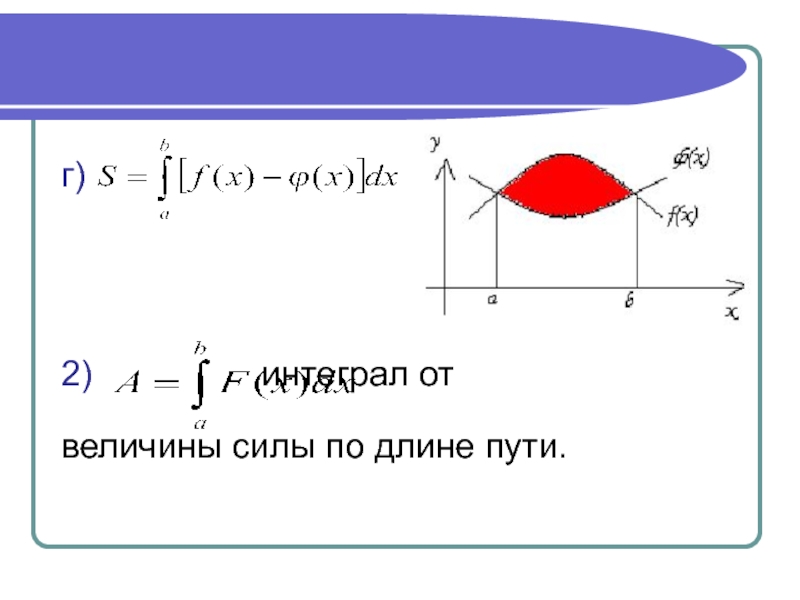
18. г)2) интеграл от величины силы по длине пути.
19. 3) Прирост численности популяции. N(t) прирост численности за
20. Скачать презентанцию

ПЛАНПонятие определенного интеграла.Свойства определенного интеграла.Метод замены переменной.Несобственные интегралы.Приложения определенного интеграла.

Главная
Разное
Определенный интеграл. Формула Ньютона- Лейбница. Приложения определенного интеграла

Слайды и текст этой презентации

Слайд 1Тема:
Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного

интеграла.

Слайд 2
ПЛАН
Понятие определенного интеграла.
Свойства определенного интеграла.
Метод замены переменной.
Несобственные интегралы.
Приложения определенного интеграла.

ПЛАНПонятие определенного интеграла.Свойства определенного интеграла.Метод замены переменной.Несобственные интегралы.Приложения определенного интеграла.

Слайд 3

1. Понятие определенного интеграла
К понятию определенного интеграла приводит задача нахождения

площади криволинейной трапеции.
Пусть на некотором интервале [a,b] задана непрерывная функция
Задача:
Построить

ее график и найти F площадь фигуры, ограниченной этой кривой, двумя прямыми x = a и x = b, а снизу – отрезком оси абсцисс между точками x = a и x = b.

1. Понятие определенного интегралаК понятию определенного интеграла приводит задача нахождения площади криволинейной трапеции.Пусть на некотором интервале [a,b]

Слайд 4Фигура aABb называется криволинейной трапецией

Слайд 5

Def.
Под определенным интегралом

от данной непрерывной функции f(x) на данном отрезке [a;b] понимается соответствующее приращение ее первообразной, то есть

Числа a и b – пределы интегрирования, [a;b] – промежуток интегрирования.

Слайд 6Правило:
Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего

и нижнего пределов интегрирования.
Введя обозначения для разности

Формула Ньютона – Лейбница.

Правило:Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования.Введя обозначения для разностиФормула

Слайд 7
Готфрид Вильгельм Лейбниц
(1646 – 1716 гг.)

Выдающийся немецкий мыслитель Готфрид Вильгельм

Лейбниц принадлежал к роду, известному своими учеными и политическими деятелями.

Он изобретал всевозможные универсальные приемы для решения всех задач сразу и, может быть, поэтому вслед за Паскалем стал строить вычислительные устройства.

Готфрид Вильгельм Лейбниц(1646 – 1716 гг.) Выдающийся немецкий мыслитель Готфрид Вильгельм Лейбниц принадлежал к роду, известному своими учеными

Слайд 8Исаак НЬЮТОН (Newton)
(04.01.1643 - 31.03.1727)

Английский физик и математик, создатель теоретических

основ механики и астрономии. Он открыл закон всемирного тяготения, разработал

(наряду с Г. Лейбницем) дифференциальное и интегральное исчисления, изобрел зеркальный телескоп и был автором важнейших экспериментальных работ по оптике. Ньютона по праву считают создателем "классической физики".

Исаак НЬЮТОН (Newton) (04.01.1643 - 31.03.1727) Английский физик и математик, создатель теоретических основ механики и астрономии. Он открыл закон

Слайд 92. Основные свойства определенного интеграла.
1)Величина определенного интеграла не зависит от

обозначения переменной интегрирования, т.е.

где x и t – любые

буквы.
2)Определенный интеграл с одинаковыми пределами интегрирования равен нулю

2. Основные свойства определенного интеграла.1)Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. где x и

Слайд 103) При перестановке пределов интегрирования определенный интеграл меняет свой знак на

обратный

(свойство аддитивности)
4) Если промежуток [a;b] разбит на конечное число частичных

промежутков, то определенный интеграл, взятый по промежутку [a;b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

3) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный (свойство аддитивности)4) Если промежуток [a;b] разбит на

Слайд 115)Постоянный множитель можно выносить за знак определенного интеграла.

6)Определенный интеграл от

алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической

сумме определенных интегралов от этих функций.

5)Постоянный множитель можно выносить за знак определенного интеграла.6)Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен

Слайд 123. Замена переменной в определенном интеграле.
где
для

, функции и

непрерывны на .

Пример: =

=

3. Замена переменной в определенном интеграле. где для , функции

Слайд 134. Несобственные интегралы.
Def: Пусть функция f(x) определена на бесконечном интервале [a;

+ ∞) и интегрируется на любом интервале [a;b], где b

< + ∞. Если существует
,

то этот предел называется несобственным интегралом функции f(x) на интервале

[a; + ∞) и обозначается .

4. Несобственные интегралы.Def: Пусть функция f(x) определена на бесконечном интервале [a; + ∞) и интегрируется на любом интервале

Слайд 14Таким образом, по определению,

Если этот предел - некоторое число, то

интеграл

называется сходящимся, если предела не существует, или он равен ∞,

то говорят, что интеграл расходится.

Таким образом, по определению, Если этот предел - некоторое число, то интеграл называется сходящимся, если предела не существует, или

Слайд 15ПУАССОН, СИМЕОН ДЕНИ (Poisson, Simeon-Denis)
(1781–1840 гг.)

Французский математик, механик и

физик. В 1811 он вывел получившее широкое применение уравнение, связывающее

электрический потенциал с плотностью пространственного распределения заряда (уравнение Пуассона).

ПУАССОН, СИМЕОН ДЕНИ (Poisson, Simeon-Denis) (1781–1840 гг.) Французский математик, механик и физик. В 1811 он вывел получившее широкое

Слайд 16Интеграл Пуассона:

если а = 1, то

Интеграл сходится, и его значение

.

Слайд 175. Приложения определенного интеграла
1) Площадь плоских фигур.
а) если

б) если

в)

Слайд 18г)

2) интеграл от

величины силы по длине пути.

Слайд 193) Прирост численности популяции.
N(t) прирост численности за промежуток времени от

t0 до T, v(t) – скорость роста некоторой популяции.

интеграл от скорости

по интервалу времени ее размножения.

3) Прирост численности популяции. N(t) прирост численности за промежуток времени от t0 до T, v(t) – скорость роста

Скачать презентацию

Разделы презентаций

Определенный интеграл. Формула Ньютона- Лейбница. Приложения определенного интеграла

Содержание

Слайды и текст этой презентации

Слайд 1Тема:
Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного

интеграла.

Слайд 3

1. Понятие определенного интеграла
К понятию определенного интеграла приводит задача нахождения

площади криволинейной трапеции.
Пусть на некотором интервале [a,b] задана непрерывная функция
Задача:
Построить

Слайд 4Фигура aABb называется криволинейной трапецией

Слайд 5

Def.
Под определенным интегралом

Слайд 6Правило:
Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего

и нижнего пределов интегрирования.
Введя обозначения для разности

Формула Ньютона – Лейбница.

Слайд 7
Готфрид Вильгельм Лейбниц
(1646 – 1716 гг.)

Выдающийся немецкий мыслитель Готфрид Вильгельм

Лейбниц принадлежал к роду, известному своими учеными и политическими деятелями.

Слайд 8Исаак НЬЮТОН (Newton)
(04.01.1643 - 31.03.1727)

Английский физик и математик, создатель теоретических

основ механики и астрономии. Он открыл закон всемирного тяготения, разработал

Слайд 92. Основные свойства определенного интеграла.
1)Величина определенного интеграла не зависит от

обозначения переменной интегрирования, т.е.

где x и t – любые

Слайд 103) При перестановке пределов интегрирования определенный интеграл меняет свой знак на

обратный

(свойство аддитивности)
4) Если промежуток [a;b] разбит на конечное число частичных

Слайд 115)Постоянный множитель можно выносить за знак определенного интеграла.

6)Определенный интеграл от

алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической

Слайд 123. Замена переменной в определенном интеграле.
где
для

, функции и

Слайд 134. Несобственные интегралы.
Def: Пусть функция f(x) определена на бесконечном интервале [a;

+ ∞) и интегрируется на любом интервале [a;b], где b

Слайд 14Таким образом, по определению,

Если этот предел - некоторое число, то

интеграл

называется сходящимся, если предела не существует, или он равен ∞,

Слайд 15ПУАССОН, СИМЕОН ДЕНИ (Poisson, Simeon-Denis)
(1781–1840 гг.)

Французский математик, механик и

физик. В 1811 он вывел получившее широкое применение уравнение, связывающее

Слайд 16Интеграл Пуассона:

если а = 1, то

Интеграл сходится, и его значение

.

Слайд 175. Приложения определенного интеграла
1) Площадь плоских фигур.
а) если

б) если

в)

Слайд 18г)

2) интеграл от

величины силы по длине пути.

Слайд 193) Прирост численности популяции.
N(t) прирост численности за промежуток времени от

t0 до T, v(t) – скорость роста некоторой популяции.

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Определенный интеграл. Формула Ньютона- Лейбница. Приложения определенного интеграла

Содержание

Слайды и текст этой презентации

Слайд 1Тема:Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного

интеграла.

Слайд 3 1. Понятие определенного интегралаК понятию определенного интеграла приводит задача нахождения

площади криволинейной трапеции.Пусть на некотором интервале [a,b] задана непрерывная функция Задача: Построить

Слайд 4Фигура aABb называется криволинейной трапецией

Слайд 5 Def.Под определенным интегралом

Слайд 6Правило:Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего

и нижнего пределов интегрирования.Введя обозначения для разностиФормула Ньютона – Лейбница.

Слайд 7Готфрид Вильгельм Лейбниц(1646 – 1716 гг.) Выдающийся немецкий мыслитель Готфрид Вильгельм

Лейбниц принадлежал к роду, известному своими учеными и политическими деятелями.

Слайд 8Исаак НЬЮТОН (Newton) (04.01.1643 - 31.03.1727) Английский физик и математик, создатель теоретических

основ механики и астрономии. Он открыл закон всемирного тяготения, разработал

Слайд 92. Основные свойства определенного интеграла.1)Величина определенного интеграла не зависит от

обозначения переменной интегрирования, т.е. где x и t – любые

Слайд 103) При перестановке пределов интегрирования определенный интеграл меняет свой знак на

обратный (свойство аддитивности)4) Если промежуток [a;b] разбит на конечное число частичных

Слайд 115)Постоянный множитель можно выносить за знак определенного интеграла.6)Определенный интеграл от

алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической

Слайд 123. Замена переменной в определенном интеграле. где для

, функции и

Слайд 134. Несобственные интегралы.Def: Пусть функция f(x) определена на бесконечном интервале [a;

+ ∞) и интегрируется на любом интервале [a;b], где b

Слайд 14Таким образом, по определению, Если этот предел - некоторое число, то

интеграл называется сходящимся, если предела не существует, или он равен ∞,

Слайд 15ПУАССОН, СИМЕОН ДЕНИ (Poisson, Simeon-Denis) (1781–1840 гг.) Французский математик, механик и

физик. В 1811 он вывел получившее широкое применение уравнение, связывающее

Слайд 16Интеграл Пуассона:если а = 1, тоИнтеграл сходится, и его значение

.

Слайд 175. Приложения определенного интеграла1) Площадь плоских фигур. а) если б) если в)

Слайд 18г)2) интеграл от величины силы по длине пути.

Слайд 193) Прирост численности популяции. N(t) прирост численности за промежуток времени от

t0 до T, v(t) – скорость роста некоторой популяции.

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Тема:
Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного

Слайд 3

1. Понятие определенного интеграла
К понятию определенного интеграла приводит задача нахождения

площади криволинейной трапеции.
Пусть на некотором интервале [a,b] задана непрерывная функция
Задача:
Построить

Слайд 5

Def.
Под определенным интегралом

Слайд 6Правило:
Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего

и нижнего пределов интегрирования.
Введя обозначения для разности

Формула Ньютона – Лейбница.

Слайд 7
Готфрид Вильгельм Лейбниц
(1646 – 1716 гг.)

Выдающийся немецкий мыслитель Готфрид Вильгельм

Слайд 8Исаак НЬЮТОН (Newton)
(04.01.1643 - 31.03.1727)

Английский физик и математик, создатель теоретических

Слайд 92. Основные свойства определенного интеграла.
1)Величина определенного интеграла не зависит от

обозначения переменной интегрирования, т.е.

где x и t – любые

обратный

(свойство аддитивности)
4) Если промежуток [a;b] разбит на конечное число частичных

Слайд 115)Постоянный множитель можно выносить за знак определенного интеграла.

6)Определенный интеграл от

Слайд 123. Замена переменной в определенном интеграле.
где
для

Слайд 134. Несобственные интегралы.
Def: Пусть функция f(x) определена на бесконечном интервале [a;

Слайд 14Таким образом, по определению,

Если этот предел - некоторое число, то

интеграл

называется сходящимся, если предела не существует, или он равен ∞,

Слайд 15ПУАССОН, СИМЕОН ДЕНИ (Poisson, Simeon-Denis)
(1781–1840 гг.)

Французский математик, механик и

Слайд 16Интеграл Пуассона:

если а = 1, то

Интеграл сходится, и его значение

Слайд 175. Приложения определенного интеграла
1) Площадь плоских фигур.
а) если

б) если

в)

Слайд 18г)

2) интеграл от

величины силы по длине пути.

Слайд 193) Прирост численности популяции.
N(t) прирост численности за промежуток времени от