Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определитель n— го порядка. Решение СЛАУ по формулам Крамера
Содержание
- 1. Определитель n— го порядка. Решение СЛАУ по формулам Крамера
- 2. Определение. Перестановками из n элементов называются комбинации
- 3. Определение. Транспозицией элементов перестановки называется перемена местами
- 4. Определение. Определителем n-го порядка называется число, обозначаемое
- 5. Замечание. Все указанные
- 6. Разложение определителя по строке (столбцу)Пример. ВычислитьРешение. Разложим определитель по 2-й строке
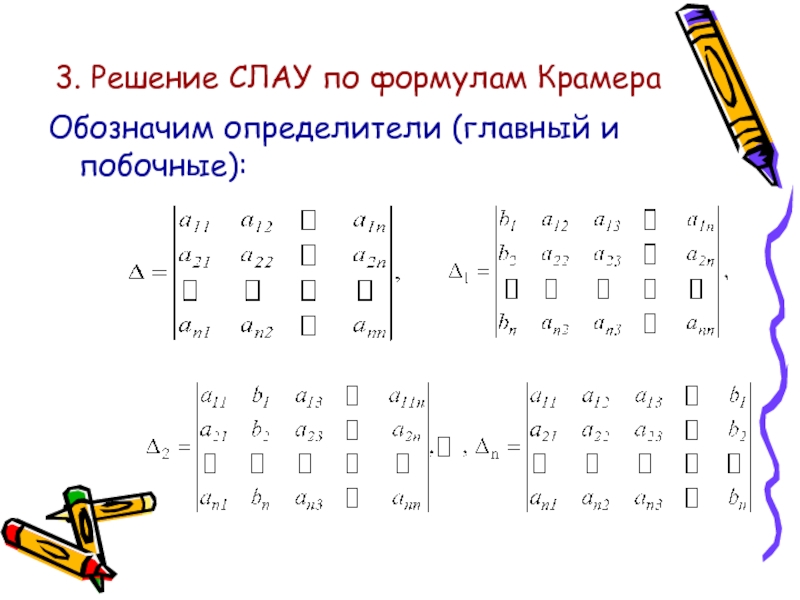
- 7. 3. Решение СЛАУ по формулам КрамераОбозначим определители (главный и побочные):
- 8. Теорема Крамера. Если главный
- 9. Док-во: Докажем формулы (2) сначала для
- 10. Следствия 1) Если главный определитель и все
- 11. Теорема 1. Если определитель однородной СЛАУ
- 12. Спасибо за внимание !
- 13. Скачать презентанцию
Определение. Перестановками из n элементов называются комбинации n различных элементов, отличающиеся порядком расположения элементов. Пример. Числовые перестановки.(1,2,3); (2,1,3); (2,3,1) –перестановки из 3-х элементов;(1,2,3,4,…,n); (2,3,1,…,n) – перестановки из n элементов.(1,2,3,…,n) – основная
Слайды и текст этой презентации
Слайд 1Определитель n—го порядка. Решение СЛАУ по формулам Крамера.
1.Некоторые сведения из
комбинаторики
Слайд 2Определение. Перестановками из n элементов называются комбинации n различных элементов,
отличающиеся порядком расположения элементов.
Пример. Числовые перестановки.
(1,2,3); (2,1,3); (2,3,1) –перестановки
из 3-х элементов;(1,2,3,4,…,n); (2,3,1,…,n) – перестановки из n элементов.
(1,2,3,…,n) – основная перестановка
Слайд 3Определение. Транспозицией элементов перестановки называется перемена местами любых 2-х элементов
перестановки («рокировка»).
Пример. Рассмотрим перестановки из 3-х элементов:
а) (1,2,3);
б) (2,1,3); в) (1,3,2) г) (3,1,2)При переходе
из а) в б) 1 транспозиция,
из а) в г) 2 транспозиции.
Слайд 4Определение. Определителем n-го порядка называется число, обозначаемое det A, равное
сумме всевозможных произведений элементов матрицы A(n x n), с
учетом числа транспозиций:
где Ni – число транспозиций, переводящих основную перестановку (1,2,..,n)
в перестановку (i1,i2,..,in)
Слайд 5Замечание. Все указанные выше свойства определителей
справедливы для определителей любого (n-го) порядка. Свойство 8) можно записать в
виде:
(а) (б)
Разложение определителя: (а) по i-й строке,
(б) по j-му столбцу.
Свойство 9)
Слайд 6Разложение определителя
по строке (столбцу)
Пример. Вычислить
Решение. Разложим определитель по 2-й
строке
Слайд 8Теорема Крамера. Если главный определитель
СЛАУ
не равен нулю, то СЛАУ имеет единственное решение, вычисляемое
по формулам:Слайд 9Док-во: Докажем формулы (2) сначала для x1 . Умножим
обе части каждого уравнения на алгебраическое дополнение 1-го коэффициента строки
и сложим все уравнения.Получим:
По свойствам определителя 8-9) имеем:
т.е.
откуда Аналогично
доказываются формулы для xj (j=2,..,n). Док-но.
Слайд 10Следствия
1) Если главный определитель и все побочные определители СЛАУ
равны нулю, то СЛАУ имеет бесчисленное множество решений.
2) Если главный определитель
СЛАУ равен нулю, но имеется побочный определитель, не равный нулю, то СЛАУ не имеет решений.Слайд 11Теорема 1. Если определитель однородной СЛАУ
не равен нулю, то СЛАУ имеет только
тривиальное (нулевое) решение.
Док-во: По теореме Крамера имеем:
Док-но.
Теорема 2. Если однородная СЛАУ имеет нетривиальное (ненулевое) решение, то её определитель равен нулю.
Док-во: (от противного).
Предположим, что определитель не равен нулю. Тогда по Теореме 1 СЛАУ имеет только нулевое решение. Но по условию, СЛАУ имеет ненулевое решение.
Получили противоречие. Следовательно, наше предположение неверно, и определитель СЛАУ равен нулю.
Док-но.