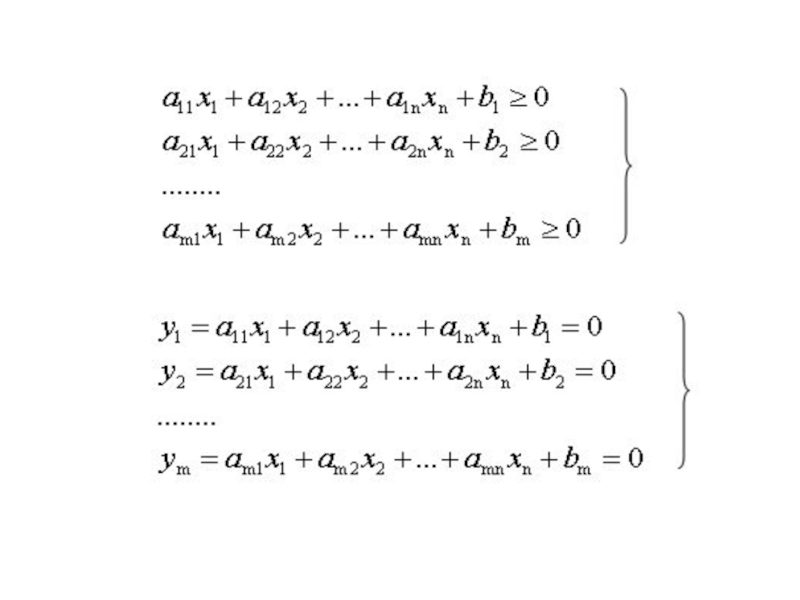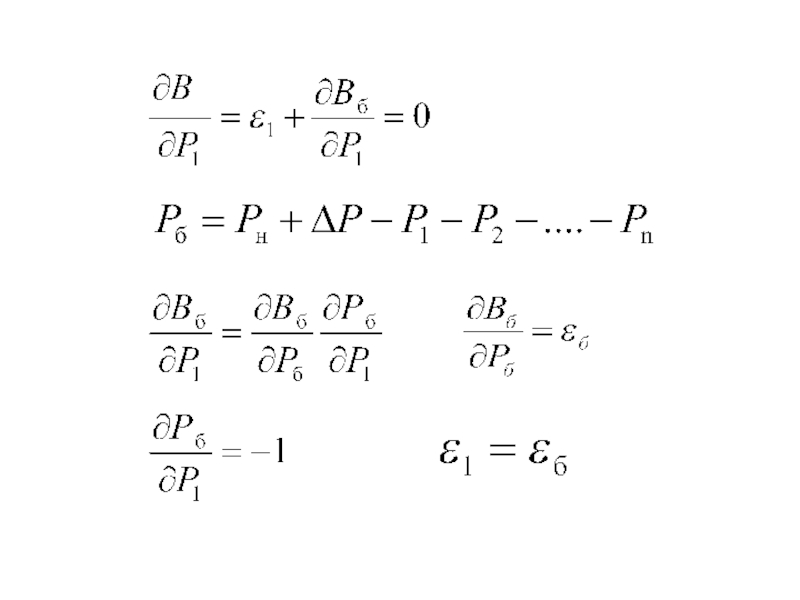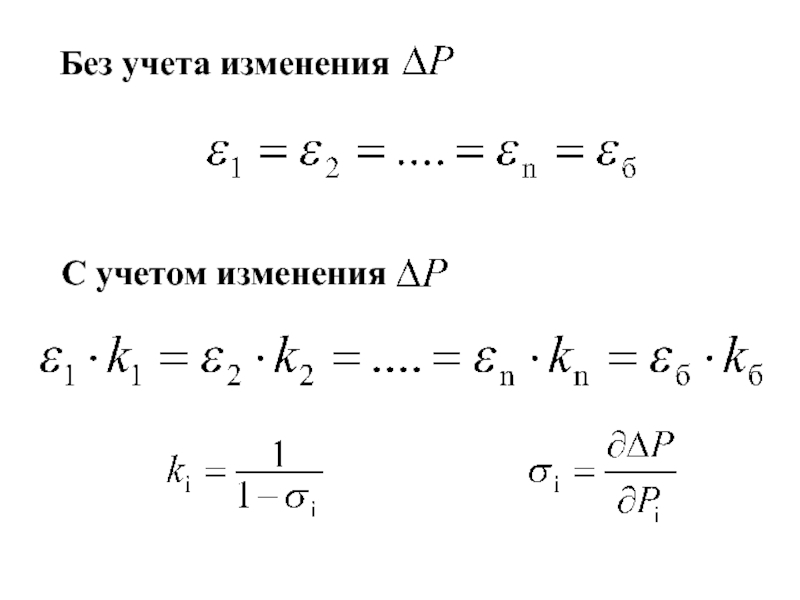Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОПТИМИЗАЦИЯ В ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМАХ Сидоркин Юрий Михайлович, кафедра
Содержание
- 1. ОПТИМИЗАЦИЯ В ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМАХ Сидоркин Юрий Михайлович, кафедра
- 2. Лекция 1 уст.
- 3. 1. Введение
- 4. Задача курсаИзучение математических методов, позволяющих вести оптимальное
- 5. ХАРАКТЕРИСТИКА ДИСЦИПЛИНЫЛекции- 6 час.Практические занятия-8час.РГРЭкзамен
- 6. СПИСОК ЛИТЕРАТУРЫОптимизация в электроэнергетических системах. Методические
- 7. Типы задач оптимизацииБалансовые задачи: распределение требуемой потребителями
- 8. Линейное программированиеНелинейное программированиеДинамическое программированиеМетоды ОПТИМИЗАЦИИ
- 9. МЕТОДЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЛП)Используются при линейной зависимости
- 10. Задачи, решаемые методами ЛПЗадача о рациональном использовании
- 11. Постановка задачи ЛП в общем виде. Задача Дж.Данцига (ОЗЛП - основная задача ЛП)
- 12. Слайд 12
- 13. Методы решения основной задачи линейного программирования (ОЗЛП)Графический
- 14. МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (НП)Применяются при нелинейном характере функции и нелинейном характере ограничений типа равенств и неравенств.
- 15. Постановка задачи оптимизацииЦелевая функцияИзвестные(заданные) переменные или функцииНезависимые
- 16. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИПри заданных условиях найти такие значения , которые обращают показатель в минимум (максимум).
- 17. Это типичная математическая задача, относящаяся к классу
- 18. 2 Методы линейного программирования 2.1 Основная задача линейного программирования (ОЗЛП)
- 19. Постановка задачи ЛП в общем виде. Задача Дж.Данцига (ОЗЛП - основная задача ЛП)
- 20. Условимся называть допустимым решение
- 21. Самый простой случай когда число независимых уравнений (m) равно числу переменных (n).
- 22. В этом случае система уравнений имеет единственное
- 23. Мы будем рассматривать случаи, когда (m
- 24. 2.2 Графическое решение ОЗЛП
- 25. Постановка задачиn переменныхm уравнений
- 26. Пусть (n-m) = 2, т.е. число переменных
- 27. Пример
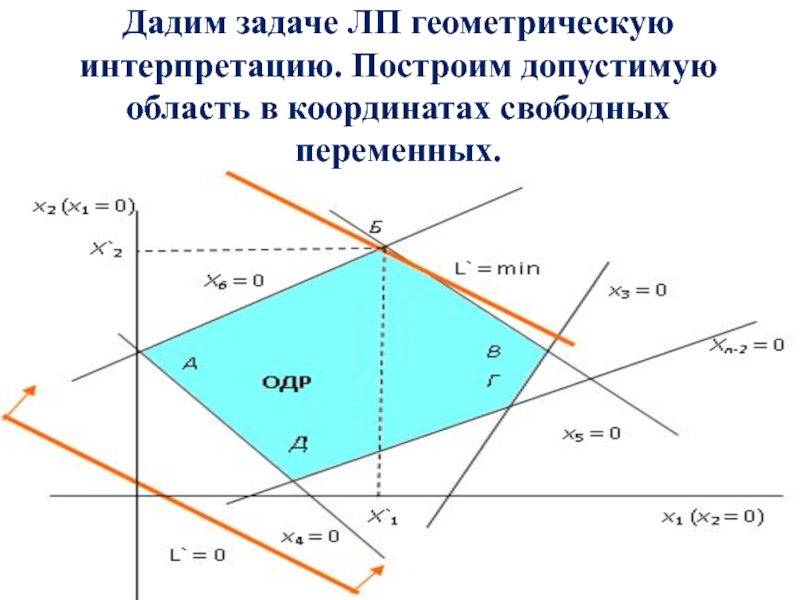
- 28. Дадим задаче ЛП геометрическую интерпретацию. Построим допустимую область в координатах свободных переменных.
- 29. Построим значения базисных переменных в координатах свободных (0x1 и 0x2)
- 30. Теперь надо найти оптимальное решение. Выразим ЦФ
- 31. Построим ЦФ (L) в координатах х1 и х2
- 32. Дадим задаче ЛП геометрическую интерпретацию. Построим допустимую область в координатах свободных переменных.
- 33. 2.3 Стандартные приемы преобразований в задачах линейного программирования
- 34. Превращение задачи на минимум в задачу на максимум и наоборот
- 35. Приведения ограничений типа равенств к стандартной форме
- 36. РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО КУРСУ Оптимизация в ЭЭС
- 37. Задание 1Оптимизировать план загрузки станций по активной
- 38. Эквивалентная схема электроэнергетической системы
- 39. Исходные данные (из учебно – методического пособия
- 40. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Необходимо дать математическую постановку задачи
- 41. Исходные данные по мощностям станций и мощности нагрузки
- 42. 2.4 Транспортная задача линейного программирования
- 43. Слайд 43
- 44. Требуется составить такой план перевозок,
- 45. Математическая формулировка задачиЧисло переменных (m+n) и все они должны быть неотрицательны.
- 46. Переменные должны удовлетворять следующим условиям 1. Суммарное
- 47. Переменные должны удовлетворять следующим условиям 2. Суммарное
- 48. Математическая формулировка задачи(2.9) (2.10)
- 49. Слайд 49
- 50. Составим транспортную таблицу
- 51. РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО КУРСУ Оптимизация в ЭЭС
- 52. Задание 2Составить оптимальный план поставок топлива на три станции от трех поставщиков.
- 53. Исходные данные (из учебно – методического пособия
- 54. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Составление оптимального плана поставок топлива
- 55. 1.1.,1.2. Составить опорный и оптимальный план поставок
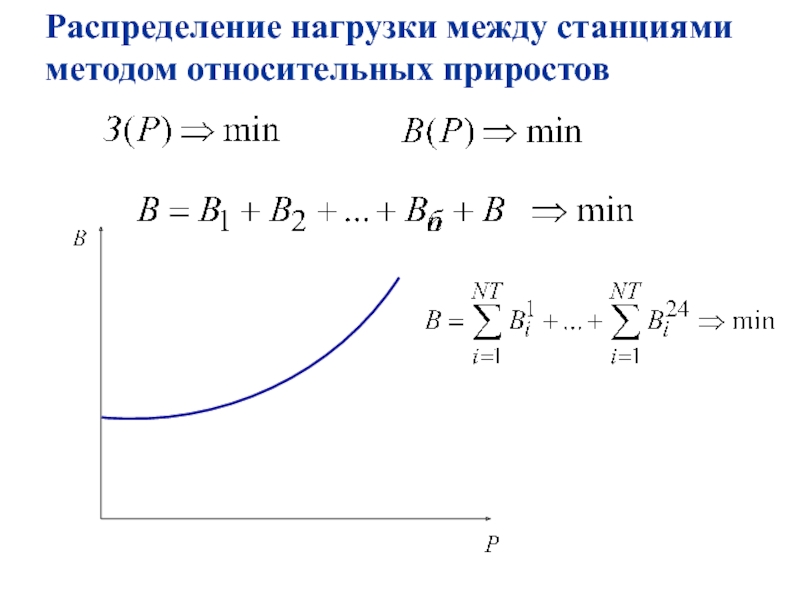
- 56. 3. Распределение нагрузки между станциями методом относительных приростов
- 57. Распределение нагрузки между станциями методом относительных приростов
- 58. Слайд 58
- 59. b
- 60. ПРИМЕР
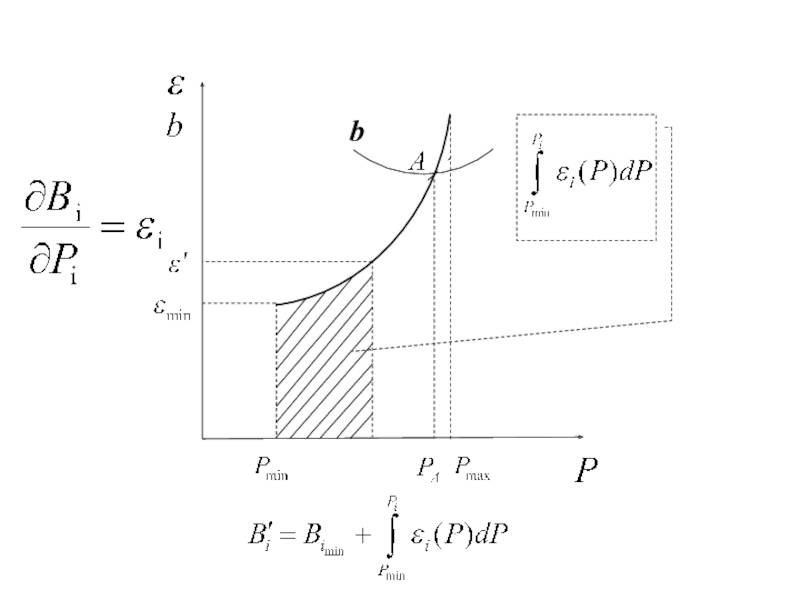
- 61. УПРОЩЕННАЯ ПОСТАНОВКА ЗАДАЧИ ЭКОНОМИЧЕСКОГО РАСПРЕДЕЛЕНИЯ НАГРУЗКИ МЕЖДУ
- 62. ЗАВИСИМАЯ ПЕРЕМЕННАЯ МОЖЕТ БЫТЬ ВЫЧИСЛЕНА ЧЕРЕЗ ОСТАЛЬНЫЕ
- 63. ЧТОБЫ НАЙТИ МИНИМУМ НАДО ПРОДИФФЕРЕНЦИРОВАТЬ ЦФ ПО НЕЗАВИСИМЫМ ПЕРЕМЕННЫМ
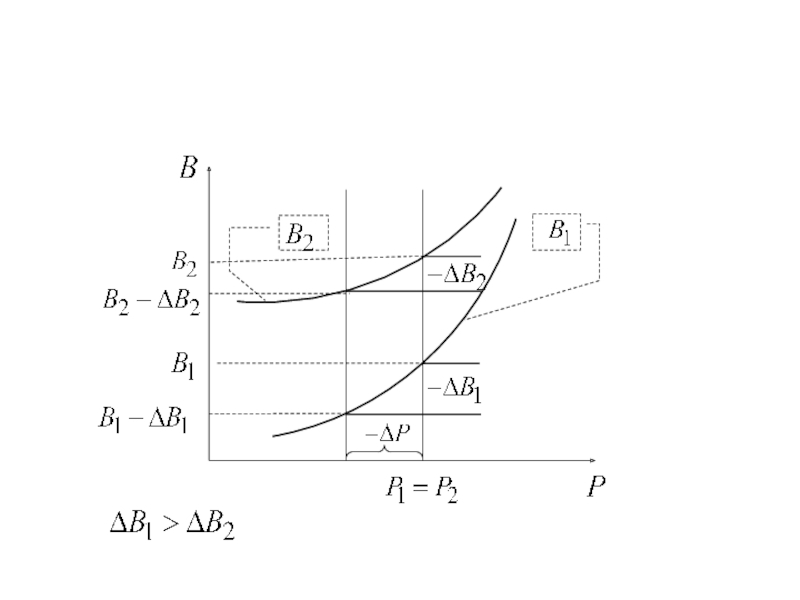
- 64. Распределение нагрузки между станциями методом относительных приростов без учёта изменения потерь мощности
- 65. Слайд 65
- 66. МИНИМУМ РАСХОДА ТОПЛИВА ДОСТИГАЕТСЯ ПРИ ТАКОМ РАСПРЕДЕЛЕНИИ НАГРУЗКИ, КОТОРАЯ СООТВЕТСТВУЕТ РАВЕНСТВУ ОТНОСИТЕЛЬНЫХ ПРИРОСТОВ РАСХОДА ТОПЛИВА
- 67. Без учета измененияС учетом изменения
- 68. РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО КУРСУ Оптимизация в ЭЭС «Оптимальное распределение мощности нагрузки в ЭЭС»
- 69. Задание 3Оптимизировать план загрузки станций по активной
- 70. Эквивалентная схема электроэнергетической системы
- 71. Исходные данные (из учебно – методического пособия
- 72. МЕТОДИЧЕСКИЕ УКАЗАНИЯ Необходимо дать математическую постановку задачи
- 73. Коэффициенты расходных характеристик станций, указанных в таблице,
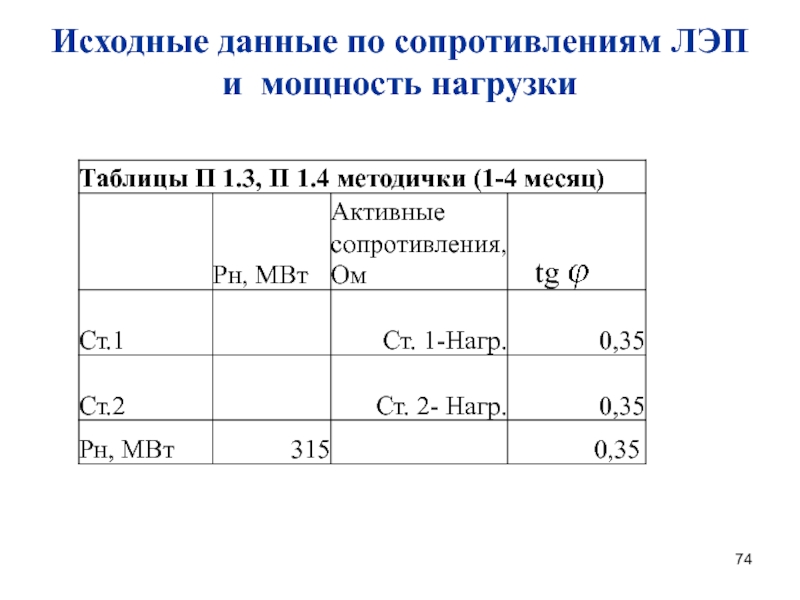
- 74. Исходные данные по сопротивлениям ЛЭП и мощность нагрузки
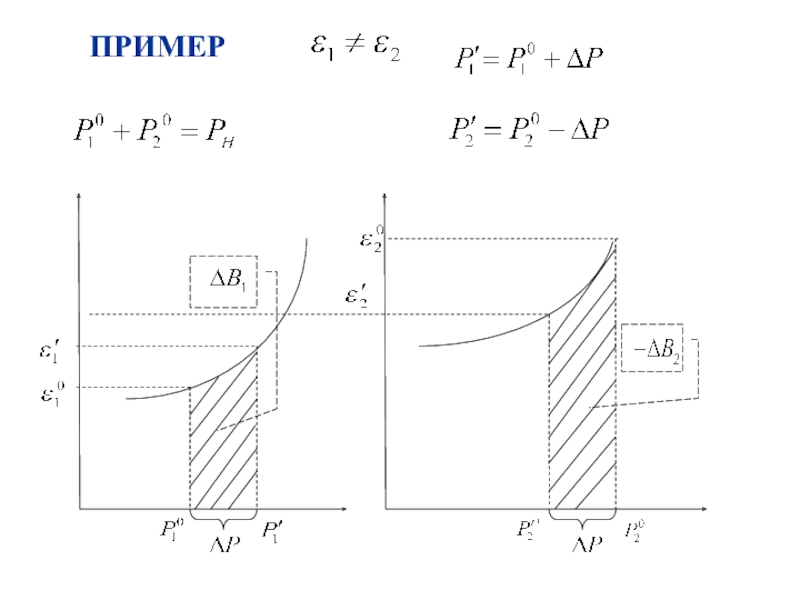
- 75. ПримерНайти оптимальную загрузку для двух параллельно работающих
- 76. Исходные данные: номинальное напряжение сети 220 кВ,
- 77. Условие оптимальности: илиДля простоты примем потери мощности равными нулю, тогда
- 78. Подставим P2 в уравнение равенства относительных приростов
- 79. ПримерНайти оптимальную загрузку для двух параллельно работающих ТЭC методом равенства относительных приростов с учётом изменения потерь
- 80. Критерий экономичности для случая учета изменения потерь
- 81. Относительные приросты потерь мощности
- 82. Рассмотрим условия предыдущего примера, добавив к ним
- 83. Относительный прирост расхода для балансирующей станции:Условие оптимальности
- 84. Условие оптимальности в нашем примере: Потери активной
- 85. Аналитическое решение этой системы уравнений затруднительно, поэтому
- 86. Получим ΔPΣ Затем найдем распределение нагрузки с
- 87. Процесс вычислений заканчивается, когда мощности станций перестанут
- 88. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4Задача курса
Изучение математических методов, позволяющих вести оптимальное управление нормальными режимами
Слайд 6 СПИСОК ЛИТЕРАТУРЫ
Оптимизация в электроэнергетических системах. Методические указания и задания
к практическим занятиям и лабораторным работам для студентов IV курса
ФЭН, направление 140200 «Электроэнергетика»,Сидоркин Ю.М., Лыкин А.В., Медведков В.В.- Новосибирск: Изд-во НГТУ, 2005 (№ 3015).Оптимизация в электроэнергетических системах. Учебно-методическое пособие ,Русина А.Г.,Сидоркин Ю.М., Лыкин А.В. ,Арестова А.Ю.,Бородин Д.Н. – Новосибирск: Изд-во НГТУ, 2015.-156 с.
Оптимизация режимов электростанций и энергосистем: Учебник / Русина А.Г., Сидоркин Ю.М., Филиппова Т.А.- Новосибирск: Изд-во НГТУ,2007.-356с.
Вентцель Е. С. Исследование операций : задачи, принципы, методология / - М., 1988. – 208с.
Слайд 7Типы задач оптимизации
Балансовые задачи: распределение требуемой потребителями мощности (электроэнергии) между
стациями и системами. Их часто называют оптимальное распределение нагрузки.
Транспортные задачи
оптимального использования ресурсов. Например, на каких шахтах закупать уголь, как распределять ограниченные материальные запасы со складов между предприятиями энергетики, как распределять ограниченные финансовые ресурсы и пр.Задачи развития: где строить станции, какие параметры ЛЭП надо выбирать, какая должна быть структура мощностей ЭЭС и др.
Слайд 8Линейное программирование
Нелинейное программирование
Динамическое программирование
Методы ОПТИМИЗАЦИИ
Слайд 9МЕТОДЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЛП)
Используются при линейной зависимости функции от искомых
неизвестных и линейном характере всех ограничений типа равенств и неравенств.
Слайд 10Задачи, решаемые методами ЛП
Задача о рациональном использовании ресурсов (сырья)
Задача о
рациональной загрузке оборудования
Транспортная задача
Задача о рациональной смеси
Слайд 13Методы решения основной задачи линейного программирования (ОЗЛП)
Графический способ решения ОЗЛП
Симплекс
– метод (табличный способ замены переменных)
Метод решения транспортной задачи ЛП
Слайд 14МЕТОДЫ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (НП)
Применяются при нелинейном характере функции и нелинейном
характере ограничений типа равенств и неравенств.
Слайд 15Постановка задачи оптимизации
Целевая функция
Известные(заданные) переменные или функции
Независимые переменные или неизвестные
переменные
Целевая функция зависит от обеих групп факторов
Слайд 16МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ
При заданных условиях
найти такие значения ,
которые обращают показатель
в минимум (максимум).
Слайд 17Это типичная математическая задача, относящаяся к классу вариационных задач.
Метод решения
- дифференцирование и приравнивание производных к нулю.
Слайд 20 Условимся называть допустимым решение (ДР) ОЗЛП любую
совокупность переменных
удовлетворяющую уравнениям (2.2).
Наличие ДР определяется только системой уравнений (2,2).Оптимальным решением будем называть то из допустимых, при котором функция (2.1) обращается в минимум.
ОЗЛП может не иметь решения, когда:
- уравнения системы (2.2) несовместны
- получаются отрицательные х (нет допустимого решения)
- функция в области допустимого решения (ДР) не ограничена с какой-то стороны (нет оптимального решения)
Слайд 22В этом случае система уравнений имеет единственное решение
Если в этом
решении хотя бы одна переменная отрицательна, то решение недопустимо и
ОЗЛП не имеет решения.Если все переменные неотрицательны, то найденное решение допустимо. Оно же является оптимальным (других нет).
Слайд 23 Мы будем рассматривать случаи, когда (m
число независимых уравнений (m) меньше числа переменных (n). Если
система уравнений совместна, у нее существует множество решений. И если значения переменных этих решений неотрицательны, то каждое из них допустимо. И задача заключается в нахождении среди допустимых оптимального. Так как число переменных больше чем число уравнений, разделим их на две группы. (n-m) переменных будем называть свободными переменными, а остальные (m) переменные будем называть базисными. Базисные будем выражать через свободные.Слайд 26Пусть (n-m) = 2, т.е. число переменных на два больше
числа независимых уравнений. В качестве свободных выберем x1 и x2. Остальные (m)
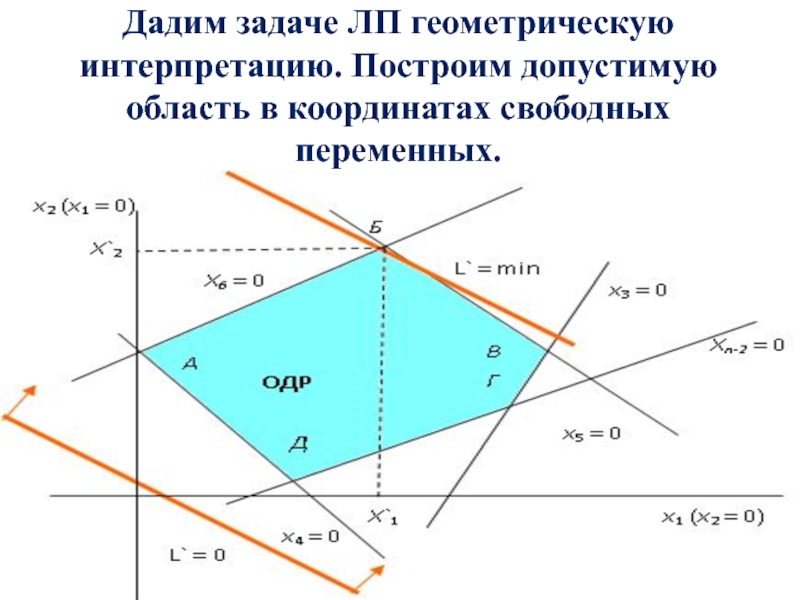
делаем базисными и выражаем их через свободные. Получили (m = n-2) уравнения.Слайд 28Дадим задаче ЛП геометрическую интерпретацию. Построим допустимую область в координатах
свободных переменных.
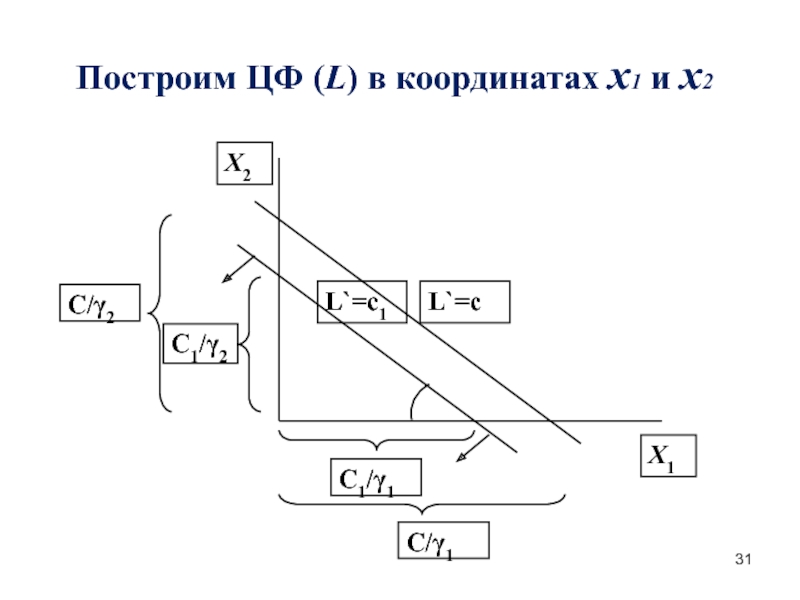
Слайд 30Теперь надо найти оптимальное решение. Выразим ЦФ через свободные переменные
и построим её в тех же координатах.
Слайд 32Дадим задаче ЛП геометрическую интерпретацию. Построим допустимую область в координатах
свободных переменных.
Слайд 36РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО КУРСУ Оптимизация в ЭЭС «Оптимальное распределение мощности
нагрузки в ЭЭС» ( вариант берёте по номеру в списке группы
на 20.06.18 г.)Слайд 37Задание 1
Оптимизировать план загрузки станций по активной мощности исходя из
максимума совокупной прибыли.
- распределить активную нагрузку между станциями
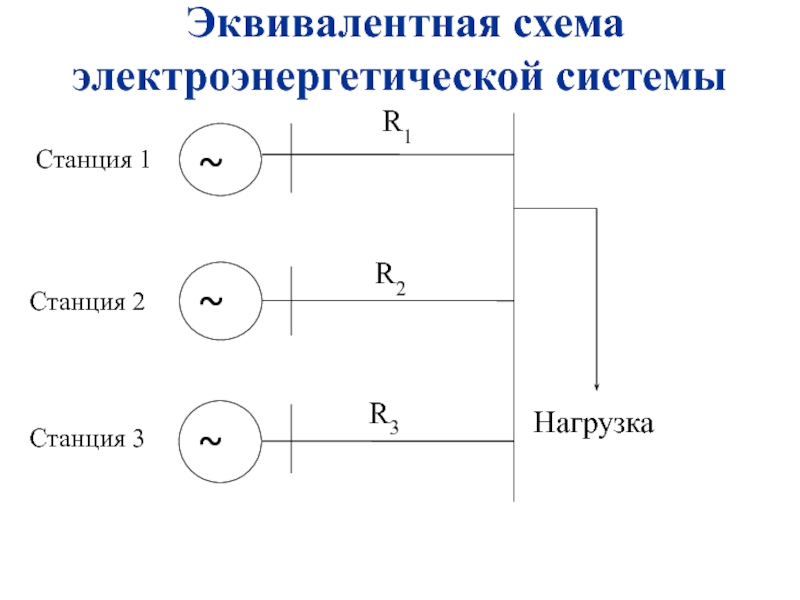
без учёта потерь мощности графическим методом решения задач линейного программирования;Слайд 39Исходные данные (из учебно – методического пособия 2015 года)
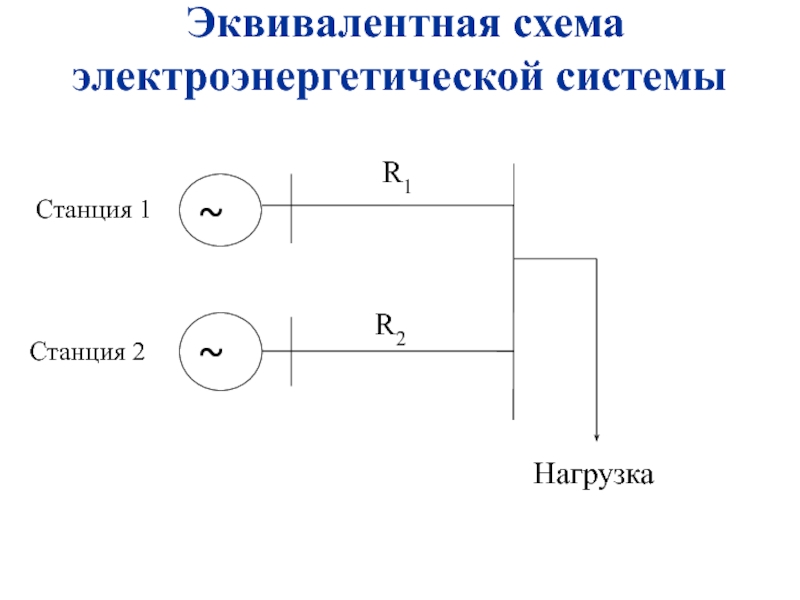
Эквивалентная
схема электроэнергетической системы
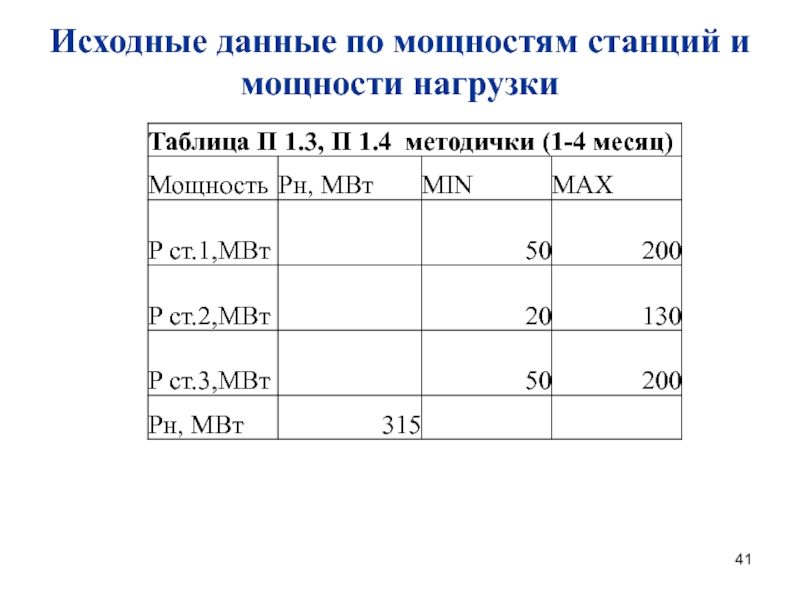
Мощность нагрузки системы
Минимальные и максимальные мощности
станций Слайд 40МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Необходимо дать математическую постановку задачи (выбрать критерий, переменные,
ограничения)
Исходные данные по минимальной и максимальной мощности станций взять
из табл. П 1.3 методического пособияИсходные данные по мощности нагрузки взять из табл. П 1.4 методического пособия (данные только по 1-4 месяцу)
Пример решения дан в параграфе 1.3 методического пособия
Определить эффект от оптимизации. Эффект определяется расчётом прибыли от продажи мощности станциями (L). Т0 из табл. П 1.2
Слайд 43
Формулировка задачи
Имеется m пунктов отправления А1 ,А2 ….Аm , в
которых имеются запасы товара а1,а2 ….аm Имеется n пунктов назначения В1 ,В2 ….Вn, в которых хотят получить b1 ,b2 ….bn единиц товар
Предполагается, что сумма всех заявок равна сумме всех запасов
Известна стоимость перевозок единицы товара Cij от каждого Аi до каждого Вj
Обозначим хij количество груза, отправляемого из i - го пункта отправления Ai в j –й пункт назначения Bj
Слайд 44 Требуется составить такой план перевозок, при котором все заявки
были бы выполнены, и при этом общая стоимость всех перевозок
была бы минимальна, то есть сумма величин хij, умноженная на соответствующие стоимости Cij должна быть минимальна (это содержательная постановка задачи)Слайд 45Математическая формулировка задачи
Число переменных (m+n) и все они должны быть
неотрицательны.
Слайд 46Переменные должны удовлетворять следующим условиям 1. Суммарное количество груза, направляемого из
каждого пункта отправления во все пункты назначения должно быть равно
запасу груза в данном пункте.(2.7)
Слайд 47Переменные должны удовлетворять следующим условиям 2. Суммарное количество груза, доставляемого в
каждый пункт назначения изо всех пунктов отправления должно быть равно
заявке, поданной данным пунктом.(2.8)
Слайд 49
Условимся:
Значения хij - количество единиц груза
из пункта Ai в пункт Bj будем называть перевозками.Любую совокупность значений хij будем называть планом перевозок.
Допустимый план – план, удовлетворяющий условиям (2.7) и (2.8).
Допустимый план называется опорным, если в нем отличны от нуля не более (r =m+n-1) базисных переменных, а остальные равны нулю. Если отличных от нуля перевозок менее чем (r=m+n-1), то такой план называется вырожденным опорным планом.
Оптимальный план – это план с наименьшей стоимостью перевозок.
При решении такой задачи не требуется работа с симплекс – таблицами, достаточно составить транспортную таблицу.
Слайд 51РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО КУРСУ Оптимизация в ЭЭС «Оптимальное распределение мощности
нагрузки в ЭЭС» (транспортная задача) Теория в главе 3 (стр. 17-20), пример
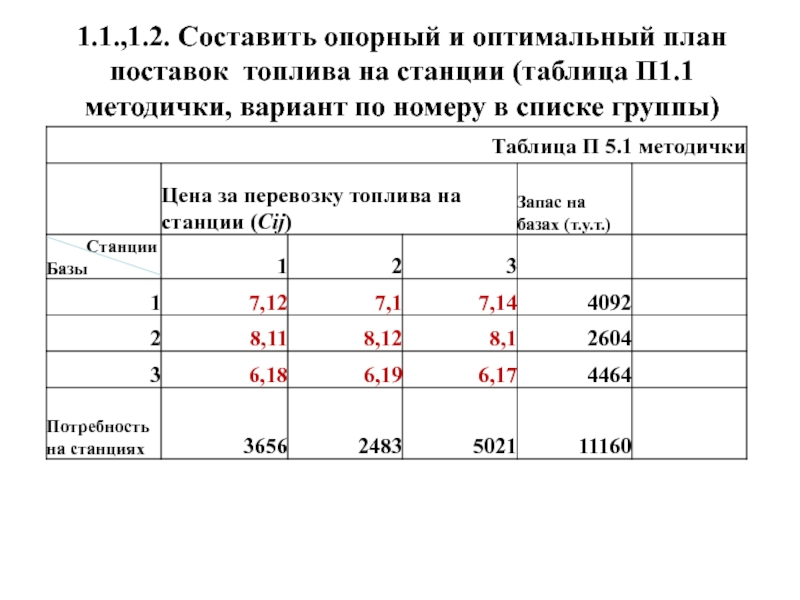
выполнения в приложении 5, п.1.1 (стр. 133-135) методического пособия 2015 г.Слайд 53Исходные данные (из учебно – методического пособия 2015 года)
Характеристики системы топливоснабжения (табл. П 1.1)- запасы топлива на трёх
базах, потребность трёх станций в топливе, цены за перевозку топлива с баз на станции.Слайд 54МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Составление оптимального плана поставок топлива на станции.
1.1. Составить
опорный план перевозок по методу северо – западного угла. План
составляется на основании данных табл. П 1.1.1.2 Составить оптимальный план перевозок используя метод потенциалов .
Необходимо:
дать математическую постановку задачи;
привести результат решения в виде таблицы (П 5.1 методички) с указанием запасов топлива на базах, потребностей станций, объемов перевозок и стоимости перевозок.
1.3. Определить и сравнить годовые издержки системы на топливо (общая стоимость перевозок) для опорного и оптимального планов.
Слайд 551.1.,1.2. Составить опорный и оптимальный план поставок топлива на станции
(таблица П1.1 методички, вариант по номеру в списке группы)
Слайд 61УПРОЩЕННАЯ ПОСТАНОВКА ЗАДАЧИ ЭКОНОМИЧЕСКОГО РАСПРЕДЕЛЕНИЯ НАГРУЗКИ МЕЖДУ СТАНЦИЯМИ ПО МЕТОДУ
ОТНОСИТЕЛЬНЫХ ПРИРОСТОВ
Найти такие значения активных мощностей станций, которые обращают в
минимум суммарный расход топлива в системе с учетом уравнения баланса Слайд 64Распределение нагрузки между станциями методом относительных приростов без учёта изменения
потерь мощности
Слайд 66МИНИМУМ РАСХОДА ТОПЛИВА ДОСТИГАЕТСЯ ПРИ ТАКОМ РАСПРЕДЕЛЕНИИ НАГРУЗКИ, КОТОРАЯ СООТВЕТСТВУЕТ
РАВЕНСТВУ ОТНОСИТЕЛЬНЫХ ПРИРОСТОВ РАСХОДА ТОПЛИВА
Слайд 68РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО КУРСУ Оптимизация в ЭЭС «Оптимальное распределение мощности
нагрузки в ЭЭС»
Слайд 69Задание 3
Оптимизировать план загрузки станций по активной мощности для схемы
из двух станций:
- распределить активную нагрузку между станциями
без учёта потерь мощности методом относительных приростов;- распределить активную нагрузку между станциями с учётом потерь мощности методом относительных приростов.
Слайд 71Исходные данные (из учебно – методического пособия 2015 года)
Эквивалентная
схема электроэнергетической системы номинальным напряжением 220кВ;
Мощность нагрузки системы (из табл.
П 1.4 взять данные только по 1 – 4 месяцу);Активные сопротивления ЛЭП (из табл. П 1.3).
Расходные характеристики станций (табл. П 1.2);
Слайд 72МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Необходимо дать математическую постановку задачи (выбрать критерий, переменные,
ограничения) и получить условия оптимальности
2. Исходные данные взять
для 1-4 месяца из табл. П 1.2, П 1.3 и П 1.4 3. Пример решения дан в параграфах 4.2 и 4.3 методического пособия
4. Определить эффект от оптимизации. Эффект определяется определением прибыли от реализации мощности системой (П), (Т0 из табл. П 1.2).
Слайд 73Коэффициенты расходных характеристик станций, указанных в таблице, надо исправить умножением на
10 в указанной степени (красным)
Слайд 75Пример
Найти оптимальную загрузку для двух параллельно работающих ТЭС. Схема содержит
две станции (узлы 1 и 2) и одну нагрузку.
Слайд 76Исходные данные: номинальное напряжение сети 220 кВ, нагрузка Sн =
Pн + jQн = 100 + j60 МВ·А.
Расходные характеристики станций:
Решение
Найдем
характеристики относительных приростов станций.Слайд 78Подставим P2 в уравнение равенства относительных приростов и получим уравнение
с одним неизвестным P1
После приведения подобных членов и подстановки Pн
= 100 Вт, получим квадратное уравнение:решение которого дает P1 = 46,177 МВт, после чего находим P2 = 100 – 46,177 = 53,823 МВт.
Слайд 79Пример
Найти оптимальную загрузку для двух параллельно работающих ТЭC методом равенства
относительных приростов с учётом изменения потерь
Слайд 82Рассмотрим условия предыдущего примера, добавив к ним
дополнительные данные: U1
= 220 кВ, U2 = 242 кВ.
R1 = 2
Ом, R2 = 5 Ом, Q1 = 35 МВАр, Q2 = 30 МВАр. Нагрузка Sн = Pн + jQн = 100 + j60 МВ·А.
Решение
Найдем характеристики относительных приростов станций.
Слайд 83Относительный прирост расхода для балансирующей станции:
Условие оптимальности
для этого случая
записывается следующим образом
Балансирующей будем считать вторую станцию.
Слайд 84Условие оптимальности в нашем примере:
Потери активной мощности в сети
и относительный прирост потерь мощности будем определять по выражениям
Слайд 85Аналитическое решение этой системы уравнений затруднительно, поэтому её лучше решить
итеративно последовательными приближениями к решению.
Для лучшей эффективности процесса решения зададим
нулевое приближение к решению следующим образом: вначале найдем решение как в случае без учета изменения потерь в сети, но не с нулевыми потерями, как ранее, а полученными по потокам мощности в сети из предыдущего решения:P1 = 46,177 МВт
и P2 = 53,823 МВт.
Слайд 86Получим ΔPΣ
Затем найдем распределение нагрузки с учётом
найденных потерь
Далее выполняем несколько итераций, в каждой из которых
вычисляем:
1. Относительную
величину прироста потерь σ;2. Мощность P1, путем решения уравнения
3. Мощность балансирующей станции
4. Потери мощности ΔPΣ и возврат к пункту 1.
Слайд 87Процесс вычислений заканчивается, когда мощности
станций перестанут изменяться сколь либо
значительно,
например, на величину не более 0,1 МВт.
Решение с учётом
изменения потерь: P1=46,3 МВт,P2=54,14 МВт, ΔPΣ =0,442 МВт.