Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОПТИМІЗАЦІЙНІ ЕКОНОМІКО-МАТЕМАТИЧНІ МОДЕЛІ
Содержание
- 1. ОПТИМІЗАЦІЙНІ ЕКОНОМІКО-МАТЕМАТИЧНІ МОДЕЛІ
- 2. ПланОсновні відомості про оптимізаціюМатематичні моделі економічних задач. Оптимізаційні моделіПриклади оптимізаційних задачТеорія двоїстості Розв’язок оптимізаційних задач
- 3. Основні відомості про оптимізацію
- 4. Теорія оптимізації є математичною дисципліною, що займається вивченням та дослідженням екстремальних задач та розробкою методів їх розв'язку.
- 5. Математично формалізована задача оптимізації в загальному вигляді
- 6. Дослідженням та розв’язком оптимізаційних задач займається спеціальна
- 7. Математична модель будь-якої задачі лінійного програмування містить:Цільову
- 8. В загальному вигляді модель задачі лінійного програмування зводиться до наступного:
- 9. Або за іншою формою запису
- 10. Матрична форма запису Знайти оптимум функції F=CX за умов AX=B
- 11. Приклади задач лінійного програмуванняЗадачі планування виробництваЗадачі складання раціону(сумішей)Транспортні задачі
- 12. Задача планування виробництва
- 13. Для виробництва певних товарів використовується деяка кількість
- 14. Слайд 14
- 15. Математична модель задачі планування виробництва:
- 16. де:m – кількість ресурсів, що використовуються у
- 17. Приклад задачі планування виробництваКондитерська фабрика для виготовлення
- 18. Математична модель задачі
- 19. Задача складання раціону
- 20. Для підтримки нормальної життєдіяльності людини використовуються продукти
- 21. Слайд 21
- 22. де:m – число поживних речовин, що містяться
- 23. Приклад задачі складання раціонуДля підтримки нормальної життєдіяльності
- 24. Слайд 24
- 25. Транспортна задача
- 26. У пунктах постачання А1,А2,...Аm міститься однорідний товар,
- 27. Слайд 27
- 28. m - кількість пунктів постачання ;n -
- 29. Слайд 29
- 30. Скачать презентанцию
ПланОсновні відомості про оптимізаціюМатематичні моделі економічних задач. Оптимізаційні моделіПриклади оптимізаційних задачТеорія двоїстості Розв’язок оптимізаційних задач
Слайды и текст этой презентации
Слайд 2План
Основні відомості про оптимізацію
Математичні моделі економічних задач. Оптимізаційні моделі
Приклади оптимізаційних
задач
Слайд 4Теорія оптимізації є математичною дисципліною, що займається вивченням та дослідженням екстремальних
задач та розробкою методів їх розв'язку.
Слайд 5Математично формалізована задача оптимізації в загальному вигляді має вигляд
Змінна Q
- критерій оптимізації
є кількісною характеристикою результатів, що отримуються.
Керовані змінні
х1 х2 ...хn характеризують умови, на які можна впливати з метою отримання найкращих результатів
Некеровані змінні ai βi
характеризують умови, на які не можна вплинути і які визначаються зовнішніми факторами
Слайд 6Дослідженням та розв’язком оптимізаційних задач займається спеціальна дисципліна, що носить
назву математичного програмування
В залежності від властивостей функції F та a
задачі математичного програмуванняподіляються на задачі лінійного і нелінійного (опуклого, квадратичного) програмування
окремими класами задач є задачі цілочислового, параметричного, дискретного, комбінаторного і дробово - лінійного програмування.
В залежності від властивостей змінних
вирізняють класи задач стохастичного та динамічного програмування
задачі, змінні яких змінюються у часі і процес розв'язку яких є багатоетапним відноситься до задач динамічного програмування
в задачах стохастичного програмування змінні є випадковими величинами
Слайд 7Математична модель будь-якої задачі лінійного програмування містить:
Цільову функцію (функцію мети),
максимум або мінімум (оптимум) якої потрібно знайти за умовою;
обмеження
у вигляді системи лінійних рівнянь (нерівностей);умову невід'ємності змінних.
Слайд 11Приклади задач лінійного програмування
Задачі планування виробництва
Задачі складання раціону(сумішей)
Транспортні задачі
Слайд 13Для виробництва певних товарів використовується деяка кількість різного роду ресурсів
(сировина, знаряддя, праця тощо).
Відомо:
скільки одиниць кожного ресурсу використовується для
виробництва одиниці кожного товару,запас кожного ресурсу
також прибуток від реалізації одиниці кожного товару.
З економічної точки зору задача полягає в наступному:
треба так запланувати виробництво товарів, щоб при використанні наявних ресурсів загальний прибуток від виробництва був найбільшим.
Слайд 16де:
m – кількість ресурсів, що використовуються у виробництві;
n – кількість
товарів, що можуть вироблятись з наявних ресурсів;
aij – кількість одиниць
і-го ресурсу, що використовується для виробництва одиниці j-го товару;bj-максимальна кількість одиниць і-го ресурсу, що можна використати у виробництві (запас одиниць і-го ресурсу);
cj-прибуток від реалізації одиниці j-го товару;
xj-кількість одиниці j-го товару, що планується виробити (шукані величини).
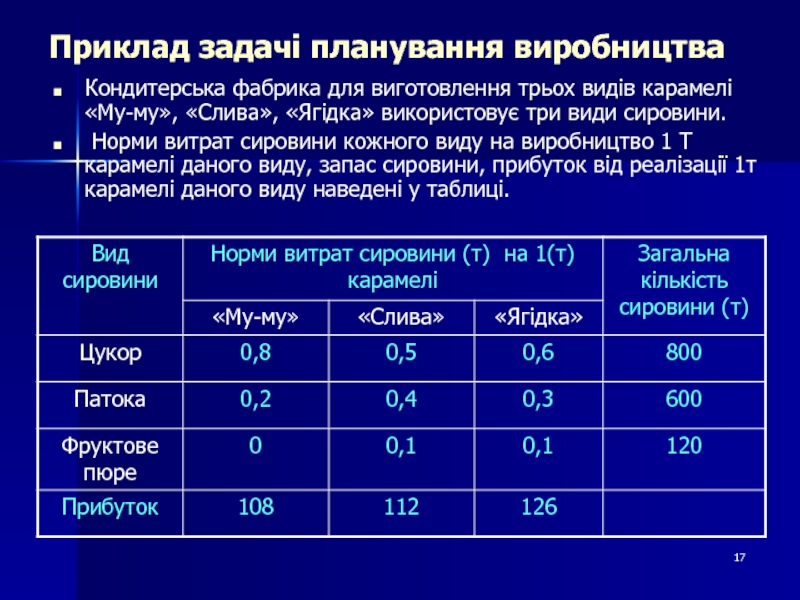
Слайд 17Приклад задачі планування виробництва
Кондитерська фабрика для виготовлення трьох видів карамелі
«Му-му», «Слива», «Ягідка» використовує три види сировини.
Норми витрат
сировини кожного виду на виробництво 1 Т карамелі даного виду, запас сировини, прибуток від реалізації 1т карамелі даного виду наведені у таблиці.Слайд 20Для підтримки нормальної життєдіяльності людини використовуються продукти харчування, що містять
у певній кількості поживні речовини.
Відомо:
скільки одиниць кожної поживної речовини
міститься в одиниці кожного продуктумінімальна добова потреба в кожній поживній речовині
вартість одиниці кожного продукту.
З економічної точки зору задача полягає в наступному: треба так скласти добовий раціон, щоб задовольнити мінімальну добову потребу в поживних речовинах і загальна вартість раціону була б мінімальною.
Слайд 22де:
m – число поживних речовин, що містяться в продуктах ;
n
– кількість продуктів, що використовуються для харчування ;
aij – кількість
одиниць і-ої поживної речовини, що міститься в одиниці j-го продукту ;bj -мінімальна добова потреба в і-ій поживній речовині при харчуванні; ;
cj- ціна j-го продукту ;
кількість одиниць j-го продукту, що планується використати в добовому раціоні (шукані величини)
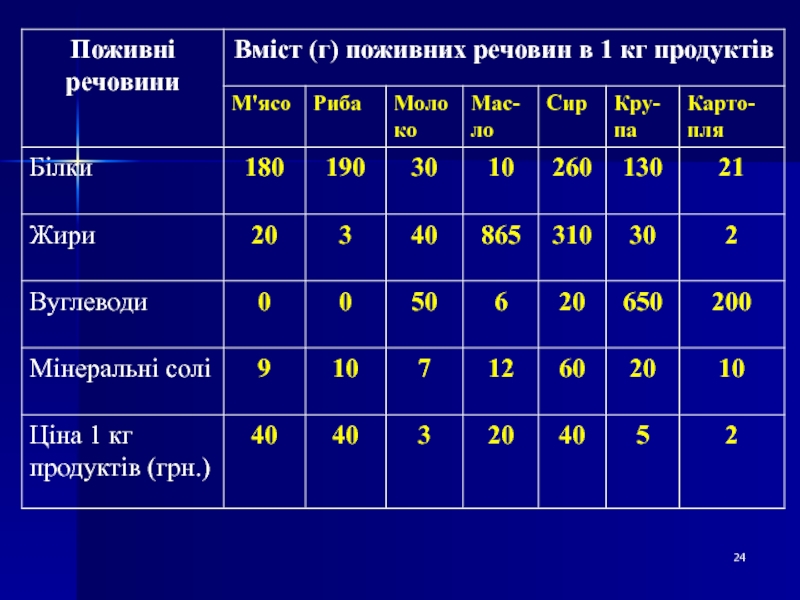
Слайд 23Приклад задачі складання раціону
Для підтримки нормальної життєдіяльності людині кожного дня
необхідно споживати не менше 118г білків, 56г жирів, 500г вуглеводів,
8г мінеральних солей.Кількість харчових речовин, що знаходяться в 1кг кожного виду продуктів, а також ціна кожного з цих продуктів наведені в таблиці.
Слайд 26У пунктах постачання А1,А2,...Аm міститься однорідний товар, що потрібно перевести
в пункти споживання В1,В2,...Вn.
Відомо:
скільки одиниць товару є в кожному
пункті постачання скільки одиниць товару потребує кожний пункт споживання
вартість переведення одиниці товару з з кожного пункту постачання в пункт споживання.
Припустимо, що виконується умова балансу
загальна кількість одиниці товару, що містять пункти постачання збігається з загальною кількістю одиниць товару, що потребують пункти споживання.
Тоді з економічної точки зору задача полягає в наступному: потрібно так запланувати перевезення товарів з пунктів постачання в пункти споживання, щоб весь товар був вивезений, всі потреби були задоволені і водночас загальна вартість усіх перевезень була б мінімальною.
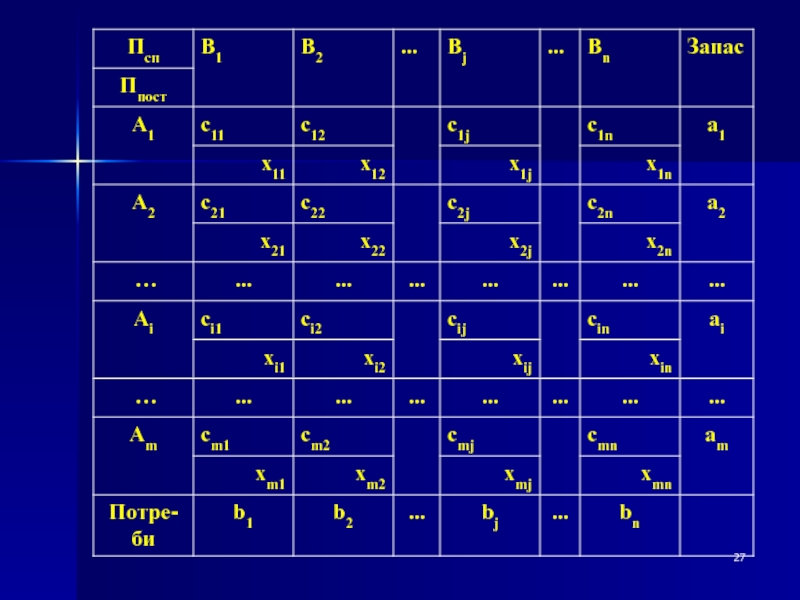
Слайд 28m - кількість пунктів постачання ;
n - кількість пунктів споживання;
ai
- кількість одиниць товару, що міститься в і-му пункті постачання;
bj
- кількість одиниць товару, що потребує j-ий пункт споживання;cij - вартість перевезення одиниці товару з і-го пункту постачання в j-ий пункт споживання;
xij - кількість одиниць товару, що планується перевезти з і-го пункту постачання в j-ий пункт споживання (шукані величини).