Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основной математический аппарат
Содержание
- 1. Основной математический аппарат
- 2. 3.1. δ – функция ДиракаВ 1930 году
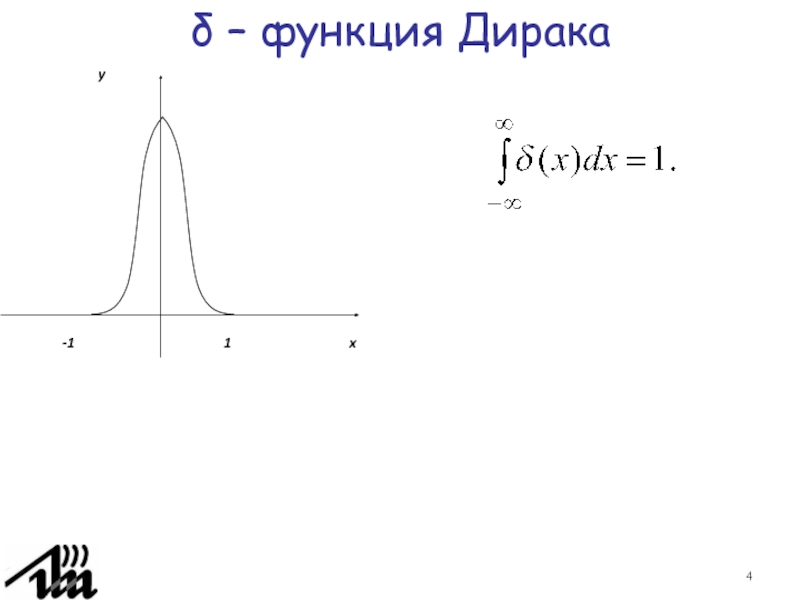
- 3. δ – функция ДиракаП. Дирак определил дельта-функцию δ(x) следующим образом: Кроме того задается условие:
- 4. δ – функция Дирака
- 5. δ – функция Дирака
- 6. кафедра ЮНЕСКО по НИТ δ – функция
- 7. кафедра ЮНЕСКО по НИТ δ – функция
- 8. кафедра ЮНЕСКО по НИТ δ – функция
- 9. Функция единичного скачкаОпределим функцию единичного скачка,
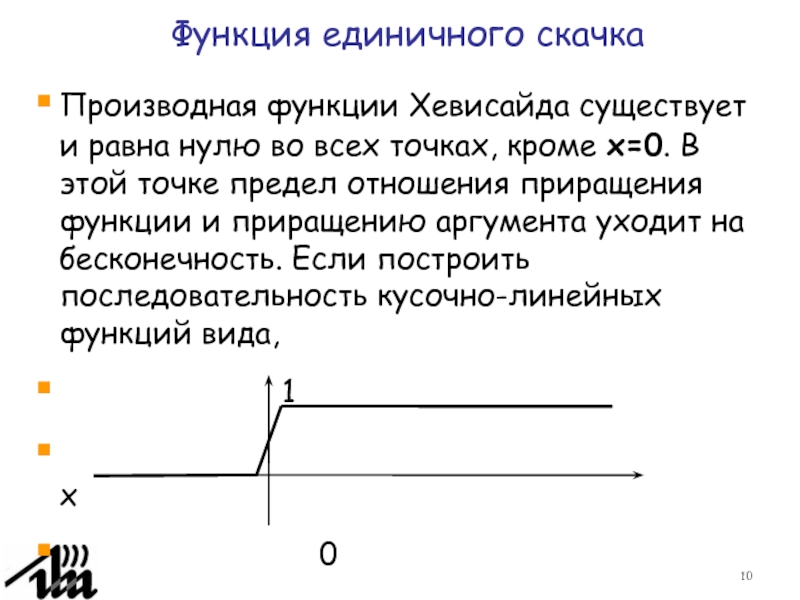
- 10. Производная функции Хевисайда существует и равна нулю
- 11. то очевидно, что производными для таких функций
- 12. 3.2. Функция распределения дискретной случайной величиныПусть
- 13. Функция распределения дискретной случайной величиныТогда функция
- 14. Функция распределения дискретной случайной величиныГрафик этой функция распределения FX(x):1/25/6FX(x)102x1
- 15. Функция распределения дискретной случайной величиныКак известно
- 16. кафедра ЮНЕСКО по НИТ Функция распределения дискретной
- 17. кафедра ЮНЕСКО по НИТВернемся к функции распределения FX(x):1/25/6FX(x)102x1 Функция единичного скачка
- 18. Функция распределения дискретной случайной величиныТакую функцию
- 19. Функция распределения дискретной случайной величиныФункцию плотности
- 20. кафедра ЮНЕСКО по НИТ Функция распределения дискретной
- 21. кафедра ЮНЕСКО по НИТ 3.2. Преобразование Лапласа
- 22. кафедра ЮНЕСКО по НИТПреобразование Лапласа L{ f(t)}
- 23. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Преобразованием
- 24. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример.
- 25. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример.
- 26. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Функция
- 27. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Найдем
- 28. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Существуют
- 29. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Свойства
- 30. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Применяя
- 31. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример.
- 32. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример.
- 33. кафедра ЮНЕСКО по НИТ Преобразование Лапласа Пример.
- 34. кафедра ЮНЕСКО по НИТ 3.3. Обратное преобразование
- 35. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа
- 36. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа Вспоминаем высшую математикуИнтегрирование функции от двух переменных по контуру0xyL
- 37. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа
- 38. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа
- 39. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа
- 40. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа
- 41. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа
- 42. кафедра ЮНЕСКО по НИТ Обратное преобразование Лапласа
- 43. Page Обратное преобразование ЛапласаПреобразование Лапласа от свертки Доказательство:
- 44. Page Обратное преобразование ЛапласаОбратное преобразование Лапласа от
- 45. Скачать презентанцию
3.1. δ – функция ДиракаВ 1930 году для решения задач теоретической физики английскому физику П. Дираку, одному из основателей квантовой механики, не хватило аппарата классической математики, и он ввел новый объект,
Слайды и текст этой презентации
Слайд 3 δ – функция Дирака
П. Дирак определил дельта-функцию δ(x) следующим
образом:
Кроме того задается условие:
Слайд 6кафедра ЮНЕСКО по НИТ
δ – функция Дирака
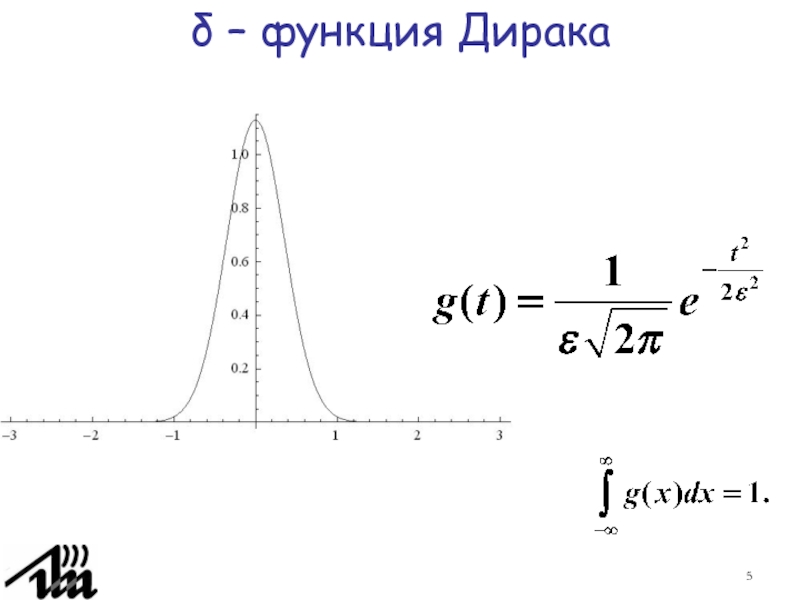
Чем более узкой
сделать полоску между левой и правой ветвью, тем выше должна
быть эта полоска, для того чтобы площадь полоски (т.е. интеграл) сохраняла свое заданное значение, равное 1. При сужении полоски мы приближаемся к выполнению условия δ(x) = 0 при x ≠ 0, то есть функция приближается к дельта-функции. Такая функция широко применяется в радиофизике.
Слайд 7кафедра ЮНЕСКО по НИТ
δ – функция Дирака
δ(x) не является
функцией в обычном смысле, так как из этого определения следуют
несовместимые условия с точки зрения классического определения функции и интеграла:при
но
В классической математике такая функция не существует
Слайд 8кафедра ЮНЕСКО по НИТ
δ – функция Дирака
Функции, из которых
предельным переходом получается δ – функция могут быть непрерывными и
разрывными.Импульс в электротехнике – это одиночный, кратковременный скачок электрического тока или напряжения.
В математической модели импульс соответствует δ – функции.
Слайд 9 Функция единичного скачка
Определим функцию единичного скачка, которая называется еще
функцией Хевисайда:
Ee график 1
x0
Слайд 10Производная функции Хевисайда существует и равна нулю во всех точках,
кроме x=0. В этой точке предел отношения приращения функции и
приращению аргумента уходит на бесконечность. Если построить последовательность кусочно-линейных функций вида,1
x
0
Функция единичного скачка
Слайд 11то очевидно, что производными для таких функций служат ступенчатые функции
(прямоугольные импульсы !), последовательность которых стремится к δ-функции. Таким образом,
производной функции Хевисайда является δ-функция.Применение функции Хевисайда и δ-функции сохраняет математических свойств в приложениях (например, в теории вероятностей) и позволяет применять аппарат математического анализа.
Функция единичного скачка
Слайд 12 3.2. Функция распределения дискретной случайной величины
Пусть дискретная случайная величина
X(ω) принимает три значения x1 = 0, x2 = 1,
x3 = 2 с вероятностями:
Слайд 13 Функция распределения дискретной случайной величины
Тогда функция распределения FX(x) дискретной
случайной величины X(ω) по определению равна FX(x) = P{X(ω) ≤
x}, она равна
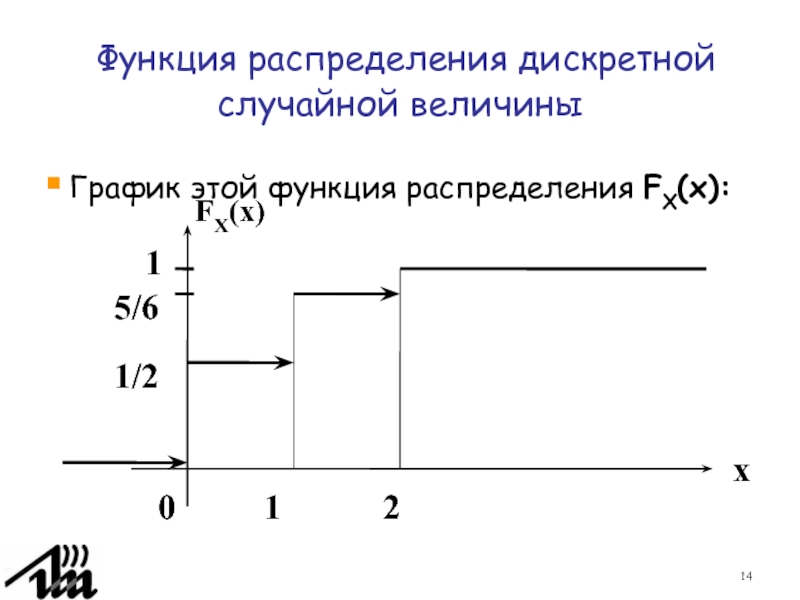
Слайд 14 Функция распределения дискретной случайной величины
График этой функция распределения FX(x):
1/2
5/6
FX(x)
1
0
2
x
1
Слайд 15 Функция распределения дискретной случайной величины
Как известно из теории вероятностей,
производной такой функция распределения FX(x) не существует, то есть случайная
величина X(ω) не имеет функции плотности распределения pX(x) = F′X(x).Но применяя δ-функцию, можно построить функции плотности распределения pX(x) и для X(ω).
Слайд 16кафедра ЮНЕСКО по НИТ
Функция распределения дискретной случайной величины
Для построения
функции плотности pX(x) вначале построим функцию распределения FX(x) с использованием
функции единичного скачкаГрафик функции а 1( x – c )
a
x
0 с
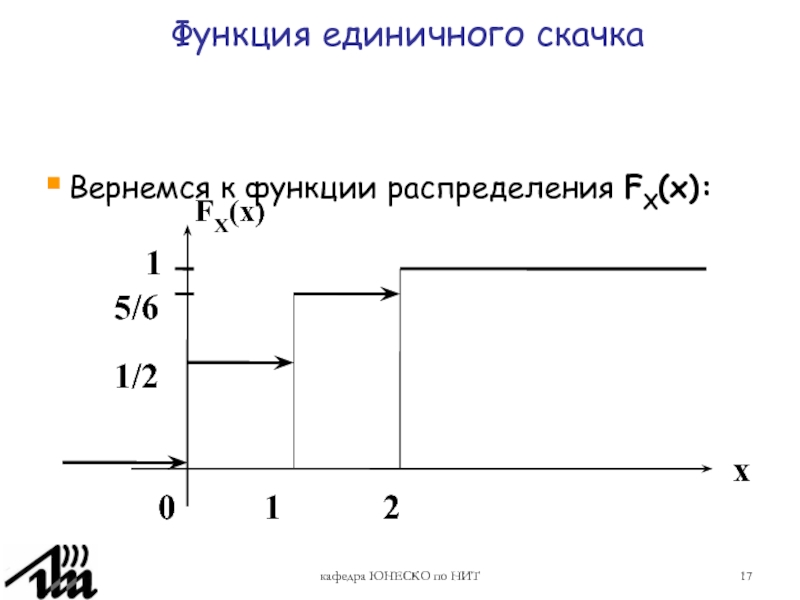
Слайд 17кафедра ЮНЕСКО по НИТ
Вернемся к функции распределения FX(x):
1/2
5/6
FX(x)
1
0
2
x
1
Функция единичного
скачка
Слайд 18 Функция распределения дискретной случайной величины
Такую функцию плотности FX(x) можно
выразить через функцию единичного скачка 1(x) . В точках разрыва
функция распределения FX(x) увеличивается на вероятность в точке разрыва, то выполняется скачок, например, в точке x=1 скачок равен 1/3. Этот скачок можно выразить функцией Хевисайда с коэффициентом 1/3.- это скачок на 1/3 в точке x=1.
Слайд 19 Функция распределения дискретной случайной величины
Функцию плотности FX(x) можно записать
через функцию единичного скачка 1(x) в следующем виде
производная функции FX(x)
:pX(x) = F′X(x) = 1/2 δ(x) + 1/3 δ(x-1) + 1/6 δ(x-2)
Слайд 20кафедра ЮНЕСКО по НИТ
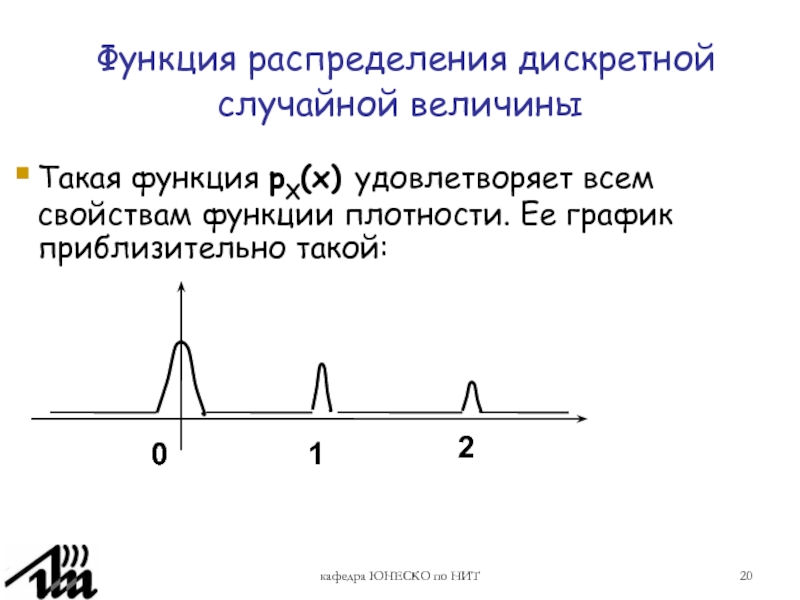
Функция распределения дискретной случайной величины
Такая функция
pX(x) удовлетворяет всем свойствам функции плотности. Ее график приблизительно такой:
0
1
2
Слайд 21кафедра ЮНЕСКО по НИТ
3.2. Преобразование Лапласа
Преобразование Лапласа применяется
для исследования дифференциальных уравнений. Оно преобразует дифференциальное уравнение в алгебраическое,
которое обычно решается проще. Затем полученное решение может быть преобразовано к решению дифференциального уравнения обратным преобразование Лапласа.
Слайд 22кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
L{ f(t)} = F(s)
Дифференц
уравнение
f(t)
Алгебраическое
уравн F(s)
Решение алг
уравнения F(s)
Решение диф
уравнение f(t)
L-1{F(s)} = f(t)
Прямое
Обратное
Слайд 23кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Преобразованием Лапласа F(s) функции
f(t), определенной для t ≥ 0, называется интегральное преобразование:
(обычно требуется
брать интеграл по частям).Переменная s комплексная, переменная t тоже может быть комплексной.
Слайд 24кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Пример. Найти преобразование Лапласа
функции единичного скачка (Хевисайда)
Решение.
При Re s > 0 этот
несобственный интеграл сходится и равен -1/s, при Re s 0 интеграл не существует. Таким образом, если Re s > 0 , то
Слайд 25кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Пример. Найти преобразование Лапласа
функции eat
Решение.
При Re (a-s) > 0 интеграл сходится.
Слайд 26кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Функция Хевисайда от аргумента
(x-a) - важная ступенчатая функция, найдем ее Лаплас-образ для a
> 0. График этой функции:1
0
a
t
Слайд 27кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Найдем преобразование Лапласа для
функции Хевисайда с параметром a>0.
Если Re s > 0, то
интеграл сходится и
Слайд 28кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Существуют таблицы преобразований Лапласа
f(t) F(s)
_ _ _ _ _ _ _ _ _ _ _ _ _
Слайд 29кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Свойства преобразования Лапласа
1. Линейность:
L(a·f(t) + b·g(t)) = a·L(f(t)) + b·L(g(t)).
2. Свойство сдвига:
если Re (s-a) > 0 и L(f) = F, то L(eat f(t)) = F(s-a).
3. Преобразование производной: L(f′) = sL(f) – f(0).
4. Преобразование интеграла:
Слайд 30кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Применяя свойство 3 найдем
преобразование Лапласа для дельта-функции δ(t - a). Эта функция является
производной от функции Хевисайда 1(t - a), для которойТогда
Слайд 31кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Пример. Применение преобразования Лапласа
к диф уравнению RC-цепи.
x(t) = С*R * y′(t) + y(t)
Применим
преобразование Лапласа к обеим частям уравнения. По свойству линейности получаем:L(x(t)) = СR L(y′(t)) + L(y(t))
По свойству преобразования производной:
L(x) = СR (sL(y)-y(0)) + L(y), пусть y(0) = k.
Отсюда L(x) = L(y)(1+CRs) – CRk
То есть
Слайд 32кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Пример. Применение преобразования Лапласа
к диф уравнению RC-цепи.
Если задана функция x(t), то это
выражение дает решение исходного дифференциального уравнения (но это Лаплас –образ решения!). Преобразование Лапласа дифференциального уравнения привело к простому алгебраическому уравнению. Теперь дело за возвратом к исходной переменной t, то есть требуется обратное преобразование.
Слайд 33кафедра ЮНЕСКО по НИТ
Преобразование Лапласа
Пример. Применение преобразования Лапласа
к диф уравнению колебания.
y′′(t) + ω2y(t) = r(t)
Дважды применяя
свойство преобразования производной, получаем
s2 Y(s) – sy(0) – y′(0) + ω2Y(s) = R(s), где Y и R обозначают Лаплас-образы соответствующих функций.
Решая полученное алгебраическое уравнение, получаем
Слайд 34кафедра ЮНЕСКО по НИТ
3.3. Обратное преобразование Лапласа
Преобразования Лапласа
содержит интеграл с пределами интегрирования от 0 до +∞. Будем
предполагать, что функция f(t) = 0 для t < 0.Обратным преобразованием Лапласа функции F(s) называется интегральное преобразование
где путь интегрирования идет вдоль прямой линии
C: Re s = c, c = const
Слайд 35кафедра ЮНЕСКО по НИТ
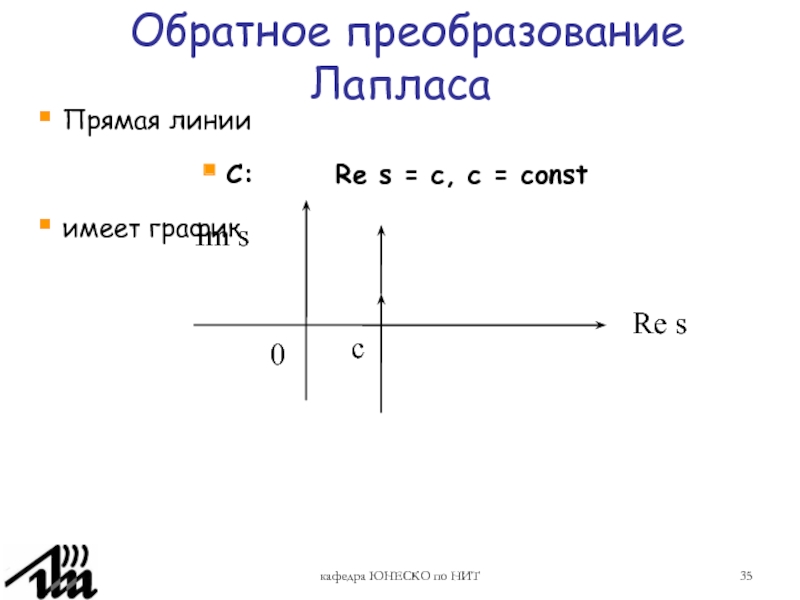
Обратное преобразование Лапласа
Прямая линии
C:
Re s = c, c = const
имеет
график0
с
Re s
Im s
Слайд 36кафедра ЮНЕСКО по НИТ
Обратное преобразование Лапласа
Вспоминаем высшую математику
Интегрирование
функции от двух переменных по контуру
0
x
y
L
Слайд 37кафедра ЮНЕСКО по НИТ
Обратное преобразование Лапласа
Вспоминаем высшую математику
Если
контур замкнут и функция f(x,y) от двух переменных имеет производные
всех порядков по x, по у и смешанные производные, то=0
0
x
y
L
Слайд 38кафедра ЮНЕСКО по НИТ
Обратное преобразование Лапласа
Вспоминаем высшую математику
Если
при этом функция f(x,y) от двух переменных имеет производные во
всех точках внутри контура, кроме точки z=(x0, y0) то= 2πi Вычет(f(z))
0
x
y
L
z
Слайд 39кафедра ЮНЕСКО по НИТ
Обратное преобразование Лапласа
Вспоминаем высшую математику
Если
, то вычет в точке a=(x0, y0) равен g(a).
0
x
y
L
z0
Слайд 40кафедра ЮНЕСКО по НИТ
Обратное преобразование Лапласа
Пример. Найти обратное
преобразование Лапласа функции
Требуется вычислить интеграл
0
с
Re s
Im s
Слайд 41кафедра ЮНЕСКО по НИТ
Обратное преобразование Лапласа
Пример. Найти обратное
преобразование для F(s)
Функцию дробно-рационального вида интегрируют простыми правилами.
F(s) разлагается в
сумму простых дробей:Коэффициенты k1, k2 вычисляются решением линейных уравнений.
Слайд 42кафедра ЮНЕСКО по НИТ
Обратное преобразование Лапласа
Пример. Найти обратное
преобразование для F(s)
Тогда Лаплас прообраз функции F(s):
Существуют таблицы обратного преобразования
Лапласа
Слайд 44Page
Обратное преобразование Лапласа
Обратное преобразование Лапласа от свертки.
Аналогично прямому преобразованию
свертки для обратного справедлива формула
L(F(s)G(s)) = f(t)*g(t)
