Слайд 1Основные понятия математической статистики
Тишков Артем Валерьевич, к.ф.-м.н., доцент
Микрюкова Надежда Николаевна
Слайд 2Основные понятия математической статистики.
Математическая статистика – это раздел математики о
методах регистрации, систематизации и анализа статистических экспериментальных данных, полученных в
результате наблюдения массовых случайных явлений.
Статистическая совокупность – это множество объектов, обладающих общими признаками, которые являются наиболее важными (типичными) для характеристики этих объектов.
Серия измерений какого либо признака совокупности – это совокупность значений случайной величины.
Объём совокупности N –это число членов совокупности.
Слайд 3Генеральная совокупность – это совокупность всех объектов, которые имеют типичную
характеристику или признак. Это все возможные значения случайной величины.
Выборочная
совокупность (выборка) – это отобранная тем или иным способом часть генеральной совокупности.
Из одной генеральной совокупности можно отбирать сколь угодно много выборок, главное, чтобы выборка была репрезентативной (представительной), а для этого элементы выборки должны отбираться случайным образом.
Варианта – это числовое значение изучаемого признака( отдельные значения случайной величины).
Слайд 4Основные задачи, которые стоят перед математической статистикой:
1. Определение закона распределения
случайной величины по имеющимся статистическим данным ( по выборке –
закон распределения для всей генеральной совокупности).
2. Определение неизвестных параметров распределения ( по выборке оценить параметры генеральной совокупности).
3. Задача проверки правдоподобия выдвигаемых статистических гипотез.
Слайд 5Схема предварительной обработки экспериментальных данных.
1) Сбор экспериментальных данных.
Чтобы определить закон
распределения случайной величины, нужно провести серию измерений или подсчётов для
интересующей нас случайной величины (признака).
В результате получаем статистический ряд – это совокупность числовых данных или выборка объёмом n:
Затем производят упорядочивание членов выборки – эта операция называется ранжирование.
Ранжирование -- это расположение всех имеющихся вариант по возрастанию. Получаем ранжированный статистический ряд.
Слайд 6Пример:
При измерении частоты пульса у 10 пациентов получены следующие результаты:
90, 110, 65, 80, 90, 60, 70, 80, 70, 80
Ранжированный ряд имеет вид: 60, 65, 70, 70, 80, 80, 80, 90, 90, 110.
Колебания изучаемого признака называются варьирование. В нашем примере варьирование - это изменение частоты пульса.
Слайд 7Схема предварительной обработки экспериментальных данных.
2) Составление вариационного ряда.
вариационный ряд (статистическое
распределение) -- набор пар значение – частота, с которой это
значение встретилось в выборке.
Если случайная величина изменяется дискретно, то составляем дискретный вариационный ряд.
Слайд 8Графическое представление дискретного вариационного ряда - это полигон частот:
х
Слайд 9Если признак изменяется непрерывно, то составляется интервальный вариационный ряд: набор
пар вид интервал – частота.
Для построения интервального вариационного ряда выборку
разбивают на интервалы. Есть несколько рекомендаций по вычислению числа интервалов:
k=log2n+1 (формула Стерджесса), k=√n и др , подробнее см.
http://ami.nstu.ru/~headrd/seminar/publik_html/Z_lab_8.htm
Длина интервала ΔX рассчитывается по формуле:
Слайд 10
Пример. Анализ веса 60-ти новорожденных дал следующие результаты: min вес
1,5 кг, max вес 5 кг.
Число интервалов берём к=7, следовательно:
Определяем границы интервалов, подсчитываем число новорожденных, вес которых попадает в каждый интервал и составляем таблицу интервальный вариационный ряд
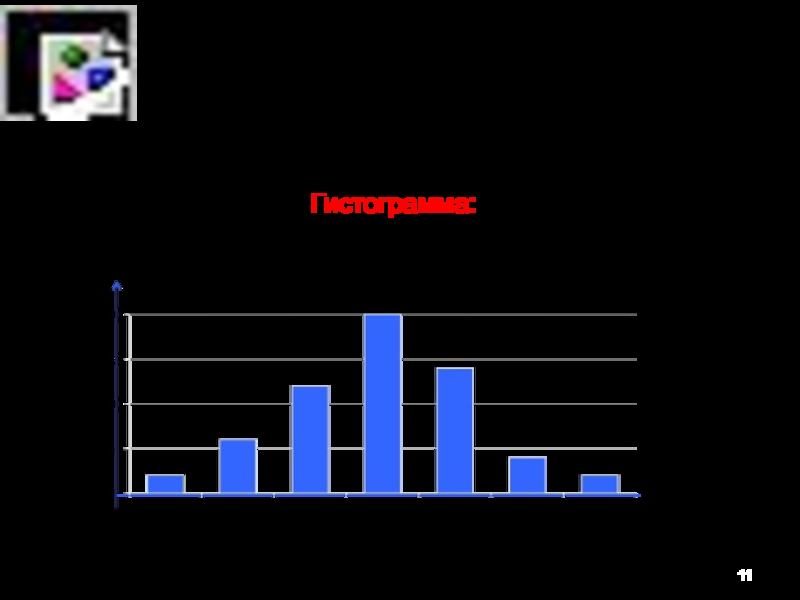
Слайд 11Графическая характеристика непрерывного вариационного ряда - Гистограмма:
Слайд 12Закономерности распределения генеральной совокупности оцениваются по выборочной совокупности.
При увеличении
объёма выборки (n→∞), относительные частоты стремятся к вероятностям соответствующих значений
с.в., то есть к закону распределения.
Слайд 13
Характеристики генеральной совокупности
Математическое ожидание M[X]
дисперсия D[X]
среднее квадратическое отклонение σ[X]
Характеристики выборки
(статистики)
- среднее арифметическое
- дисперсия
-стандартное отклонение (среднее
квадратическое)
Статистические характеристики совокупности
Слайд 14Генеральная совокупность (n→∞) Выборка (n- конечно)
ν=n-1 число степеней
свободы
Sn-стандартное отклонение
Слайд 15Извлечём из генеральной совокупности N выборок, тогда их средние арифметические
сами будут являться значениями случайной величины
Все эти значения
имеют отклонения (рассеивание) от истинного значения М[X].
Это отклонение называется ошибка среднего арифметического, она в n раз меньше отклонения каждого xi от для данной выборки объёмом n
Ошибка среднего арифметического
Слайд 16 показывает насколько выборочное среднее арифметическое близко к матожиданию
М[X] генеральной совокупности.
Чем больше объём выборки n, тем ближе среднее арифметическое к М[X] генеральной совокупности ( т.е., ошибка меньше, чем больше n). Этот вывод получил название Закон больших чисел.
Слайд 17Истинные значения М[X] и D[X] можно найти по генеральной совокупности,
что практически невозможно. По выборке из этой совокупности мы находим
лишь их точечные оценки и , но насколько их значения близки истинным М[X] и D[X]? Например, как велика разность
Поэтому наряду с точечными оценками, применяют интервальные оценки параметров генеральной совокупности по выборке.
То есть мы хотим найти интервал ΔX, такой что:
или
?
Доверительный интервал и доверительная вероятность
Слайд 18Если известна функция распределения, то этот интервал можно найти из
соотношения:
зная границы интервала, можно найти вероятность случайной величины
принимать значения из данного интервала.
Но нам требуется решить обратную задачу: определить границы интервала, следовательно, для этого надо заранее задать вероятность, с которой мы этот интервал будем определять. Эту вероятность называют доверительной вероятностью РД, а определённый с её помощью интервал -- доверительным интервалом ΔXд.
Слайд 19Доверительным интервалом какого либо параметра, называют такой интервал, о котором
можно сказать, что с вероятностью РД он содержит в себе
этот параметр.
Доверительную вероятность обычно берут равной РД=0,95, но в особо ответственных случаях принимают РД=0,99 или даже РД=0,999.
С доверительной вероятностью связан уровень значимости α=1-РД.
Уровень значимости α --это вероятность того, что значение исследуемого параметра не попадёт в доверительный интервал.
Слайд 20Основная масса случайных величин в биологии и медицине распределена по
нормальному закону распределения, следовательно, задав доверительную вероятность можно определить доверительный
интервал:
Например, при РД=0,95
отклонение для случайной величины
Но для малых выборок (n<30) распределение может значительно отличаться от нормального.
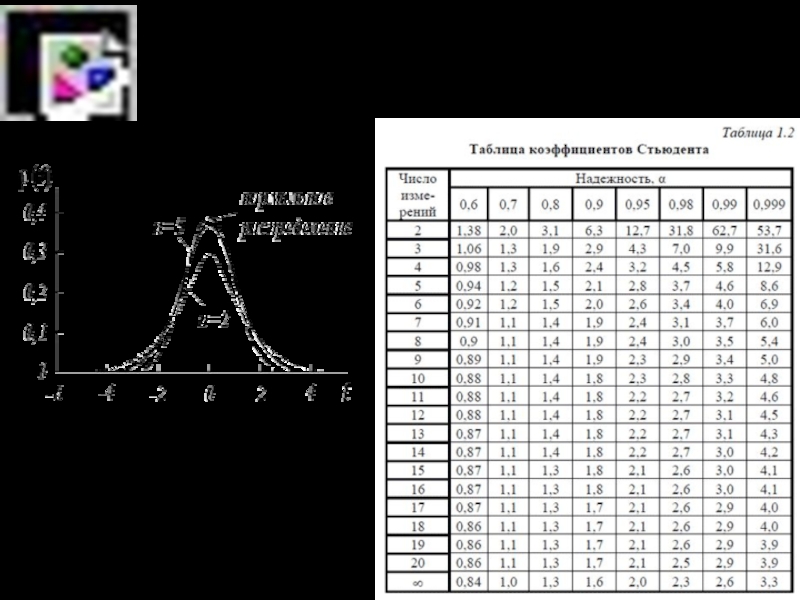
В 1908 г английский математик и химик Уильям Госсет под псевдонимом Стьюдент предложил распределение случайной величины для малых выборок.
Слайд 22
Нормированная случайная величина вычисляется по формуле:
Плотность вероятности случайной величины:
Где Вn -- параметр , зависит от n.
По мере увеличения
объёма выборок n, распределение Стьюдента довольно быстро приближается к нормальному распределению Гаусса и при n˃30 практически не отличается от него.
Распределение Стьюдента
Слайд 23Практическим следствием этого открытия явилась возможность определять границы доверительного интервала
для М[X] с заданной доверительной вероятностью РД:
коэффициент Стьюдента, находим в таблице для заданной РД и известного n.
Таким образом, определив доверительный интервал, можно записать:
Слайд 25Пример:
При определении концентрации белка в растворе были получены следующие
результаты (в мг/л):110, 112, 115, 113, 114. Найти среднее значение,
стандартное отклонение и доверительный интервал для Рд=0.95.
Слайд 27
1.Провести серию измерений, не менее трех
2.Найти среднее арифметическое
3.Вычислить доверительный
интервал (случайную ошибку).
для заданной доверительной вероятности, например,
4.Найти
систематическую ошибку.
а). если указан класс точности прибора:
Алгоритм обработки результатов прямых измерений
Слайд 28 б). если класс точности не указан ( например линейка
или термометр)
5. Вычислить общую ошибку:
Эту ошибку называют еще
абсолютной ошибкой.
6. Записать окончательный результат:
7. Кроме абсолютной ошибки желательно также найти коэффициент вариации (или относительную ошибку, выраженную в процентах):
где Х шкалы – это предел шкалы (максимальное значение на шкале)
Слайд 29Контрольные вопросы.
1.Равномерный закон распределения непрерывной случайной величины.
2.Нормальный закон распределения непрерывной
случайной величины.
3.Основные понятия математической статистики.
4.Схема предварительной обработки экспериментальных данных.
5.Статистические характеристики
совокупности.
6.Ошибка среднего арифметического.
7.Доверительный интервал и доверительная вероятность.
8.Распределение Стьюдента.








![Основные понятия математической статистики Характеристики генеральной совокупностиМатематическое ожидание M[X]дисперсия D[X]среднее квадратическое отклонение σ[X]Характеристики выборки (статистики) Характеристики генеральной совокупностиМатематическое ожидание M[X]дисперсия D[X]среднее квадратическое отклонение σ[X]Характеристики выборки (статистики) - среднее арифметическое-](/img/thumbs/93dd34c6cdd96cfa81d18f394a1f3b6b-800x.jpg)

![Основные понятия математической статистики показывает насколько выборочное среднее арифметическое близко к матожиданию М[X] генеральной показывает насколько выборочное среднее арифметическое близко к матожиданию М[X] генеральной совокупности.](/img/thumbs/76a5f1a1b5a3b03b9a2a59749298579e-800x.jpg)
![Основные понятия математической статистики Истинные значения М[X] и D[X] можно найти по генеральной совокупности, что Истинные значения М[X] и D[X] можно найти по генеральной совокупности, что практически невозможно. По выборке из этой](/img/thumbs/c7cc6a32d5196efa9de95b8209bfdf61-800x.jpg)





![Основные понятия математической статистики Практическим следствием этого открытия явилась возможность определять границы доверительного интервала для Практическим следствием этого открытия явилась возможность определять границы доверительного интервала для М[X] с заданной доверительной вероятностью РД:](/img/thumbs/0ac8f49094a1ec93dd3f9b36af987ea8-800x.jpg)