Слайд 2В системе, изображенной на рисунке, прикрепленные к невесомым пружинам грузики
при помощи нитей удерживаются на расстоянии l\2 от стенок, к
которым прикреплены концы пружин. Длины обеих пружин в недеформированном состоянии одинаковы и равны L. Нити одновременно пережигают, после чего грузики сталкиваются и слипаются. Найдите максимальную скорость, которую будут иметь грузики при колебаниях, возникших после этого столкновения. Удар при столкновении является центральным и абсолютно неупругим.
Трением и размерами грузиков пренебречь.
Задача 1.
Слайд 3Решение
Направим координатную ось вправо и поместим начало координат посередине
между стенками. Тогда после пережигания нитей левый грузик будет двигаться
по закону
X1(t)=-L\2cos(t√(2k\m)), здесь L\2 - амплитуда, √(2k\m) - частота (1)
Здесь учли, что период колебаний пружинного маятника
T=2π √(k\m), ω=2π\T, ω= √(k\m) (2)
Для второго грузика аналогично запишем
X2(t)=L\2cos(t√(k\2m))(3)
Грузики столкнутся через время t0, которое определяется из условия X1(t)=X2(t).
Слайд 4-L\2cos(t0√(2k\m))=L\2cos(t0√(k\2m)) (4)
По формуле суммы косинусов получим из
(4)
2cos(1\2(√(2k\m)+√(k\2m))t0)*2cos(1\2(√(2k\m)-√(k\2m))t0)=0 (5)
Из (5) следует, что
cos(1\2(√(2k\m)+√(k\2m))t0)=0 или
cos(1\2(√(2k\m)-√(k\2m))t0)=0 (6)
Из всех решений
выберем наименьшее положительное, которое получается из условия
1\2(√(2k\m)+√(k\2m))t0=π\2 (7)
Слайд 5Из (7) следует t0=π\3√(2k\m) (8)
В момент столкновения грузики
будут иметь координату
X0= L\2cos(t0√(k\2m)= L\2cos(π\3√(2k\m) √(k\2m))=L\4 (9)
Скорости левого и правого
грузиков перед столкновением будут равны
U1= L\2 √(2k\m)sin(t0√(2k\m))= L\2√(2k\m)(√3\2) (10)
U2=-L\2 √(k\2m)sin(t0√(k\2m))=-L\2√(k\2m)(√3\2) (11)
Скорость грузиков непосредственно после соударения найдем из закона сохранения импульса (учтем (10) и (11))
U=(mu1+2mu2)\(m+2m) (12)
Скорость грузиков после удара равна нулю, а удлинения пружин отличны от нуля и равны
X0=L\4
Слайд 6Следовательно, после столкновения слипшиеся грузики
будут совершать колебания с амплитудой
X0 и частотой
ω=√((k+2k)\(m+2m))=√(k\m) (14)
В процессе этих колебаний
максимальная скорость грузиков будет равна
Umax=ωX0=L\4√(k\m) (15)
Ответ: Umax=ωX0=L\4√(k\m)
Слайд 7Над одним молем идеального одноатомного газа совершают процесс 1-2-3-4-1. Газ
получает от нагревателя за один цикл количество теплоты Q .
Какое количество теплоты будет получать газ за один цикл, если совершать над ним процесс 2-3-4-А-В-С-2? Известно, что T3=16T1, T2=T4. Точка В – пересечение изотермы T=T2 c прямой 1-3, проходящей через начало координат pV -диаграммы. Ответ выразить через Q.
Задача 2.
Слайд 8Решение
Рассмотрим сначала исходный цикл и выразим количество теплоты через
другие параметры системы.
Q=∆U+A (1)
Теплота сообщается газу
на участках 1-2 и 2-3, следовательно, количество теплоты, сообщенное газу за один цикл
Q=Q1+Q2=3\2vR(T2-T1)+5\2vR(T3-T2) (2)
Выразим T2 через T1. Для этого рассмотрим участки 1-2 и 3-4. Запишем для них p1\T1=p2\T2, p3\T3=P4\T4 (3)
Здесь p2=p3, p1=p4, T2=T4 (4)
Тогда из (3) и (4) получаем p2\T3=p1\T2 (5)
Из (3) и (5) получим p1\p2=T1\T2=T2\T3, сл-но T2=√(T1*T3) (6)
По условию Т3=16Т1, значит Т2=4Т1. (7)
Слайд 9Из (2) с учетом (7) получим
Q=3\2vR(4T1-T1)+5\2vR(16T1-4T1)=69\2vRT1 (8)
Теперь
рассмотрим цикл 2-3-4-А-В-С-2. Теплота Q1 сообщается газу на участках С-2,
2-3, А-В. Очевидно, что Q1=Q-QAC+QAB (9)
QAC=3\2vR(Tc-T1), QAB=3\2vR(TB-TA) (10)
Выразим TA, TB, TC через Т1. По аналогии с циклом 1-2-3-4, с учетом того, что ТВ=Т2=4Т1, можно для цикла 1-С-В-А-1 записать
ТА=√(Т1ТВ)=√(Т1Т2)=2Т1=Тс (11)
Подставим (11) в (10)
Q1=69\2vRT1-3\2vR(2T1-T1)+3\2vR(4T1-2T1)=72\2vRT1 (12)
Из (8) vRT1=2\69Q, тогда Q1=24\23Q.
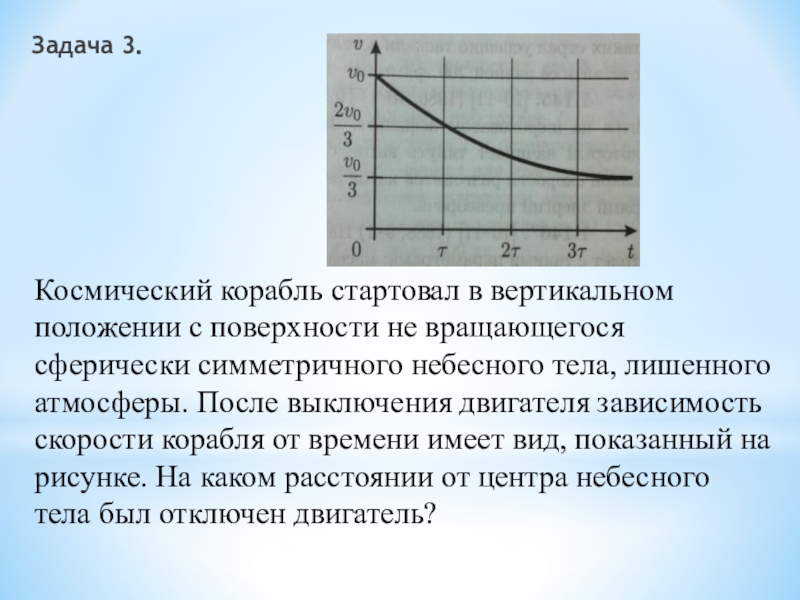
Слайд 10Космический корабль стартовал в вертикальном положении с поверхности не вращающегося
сферически симметричного небесного тела, лишенного атмосферы. После выключения двигателя зависимость
скорости корабля от времени имеет вид, показанный на рисунке. На каком расстоянии от центра небесного тела был отключен двигатель?
Задача 3.
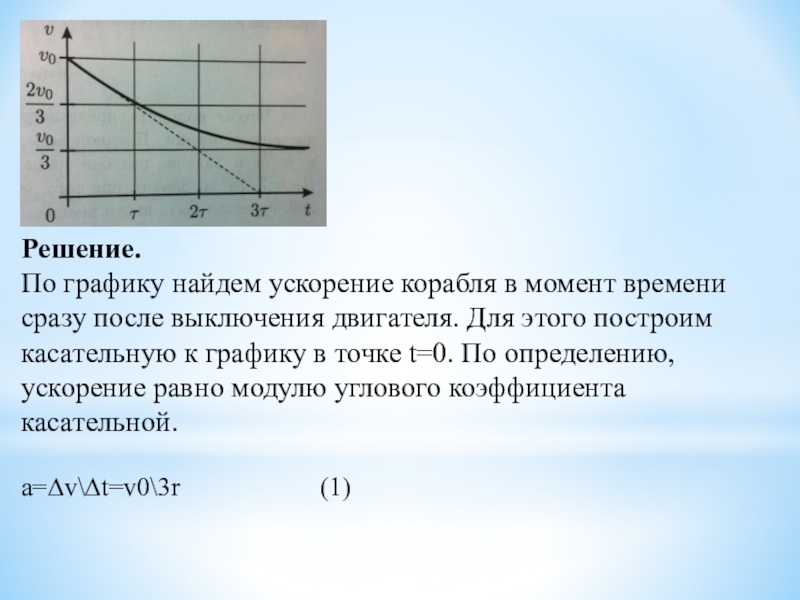
Слайд 11Решение.
По графику найдем ускорение корабля в момент времени сразу
после выключения двигателя. Для этого построим касательную к графику в
точке t=0. По определению, ускорение равно модулю углового коэффициента касательной.
а=∆v\∆t=v0\3r (1)
Слайд 12После отключения двигателя на корабль действует только гравитационная сила со
стороны небесного тела
ma=GmM\ R2 ,
(1)
Где m и M – масса корабля и масса небесного тела,
R – искомое расстояние.
После удаления корабля на очень большое расстояние от небесного тела. Его скорость стала постоянной и равна v1=v0\3. (3)
Применим закон сохранения механической энергии для корабля, находящегося в гравитационном поле планеты
mv12 \2-mv02 \2=-GmM\R2 (4)
С учетом (2) перепишем (4) mv12 \2-mv02 \2=-maR (5)
Из (5) и (1) получим
R=(v02 –v12 )\2a=3r\2v0 (v02 -v02 \9)=4\3rv0
Слайд 13Задача 4.
Длинный цилиндрический проводник, по которому идет электрический ток, охлаждается
потоком жидкости. Во сколько раз изменится перепад температуры на границе
проводник-жидкость, если радиус проводника увеличить в два раза, не изменяя его длину и приложенное к нему напряжение? Считать, то теплоотдача пропорциональна перепаду температур, а удельное сопротивление материала проводника не зависит от температуры.
Слайд 14Решение
Количество теплоты, которое выделяется на стержне
Q=(U2 \R)∆t
(1)
Увеличим радиус проводника в два раза r1=2r,
тогда
сопротивление R1=ρl\S=ρl\π(r1)2=ρl\4πr2 =R\4 –уменьшилось в 4 раза (2)
Площадь поверхности S1=2πr1h=4πrh=2S-увеличилась в два раза.
Теплоотдача по условию пропорциональна перепаду температур, следовательно Q\S ∆t =α∆T, где α-коэффициент пропорциональности. (4)
Тогда Q1\S1∆t=α∆T1 (5)
Слайд 15
Учтем (1) и (2) Q1=4Q
(6)
Тогда из (6), (5), (3) получим
Q1\S1∆t=α∆T1=4Q\S∆t=2Q\S∆t=U2\RS
(7)
Перепишем (4) Q\S∆t=α∆T=U2\RS (8)
Поделим (7) на (8) α∆T\α∆T1=(U2\RS)\(2U2\RS)1\2, тогда ∆T1=2∆T.
Ответ: перепад температур увеличится в два раза