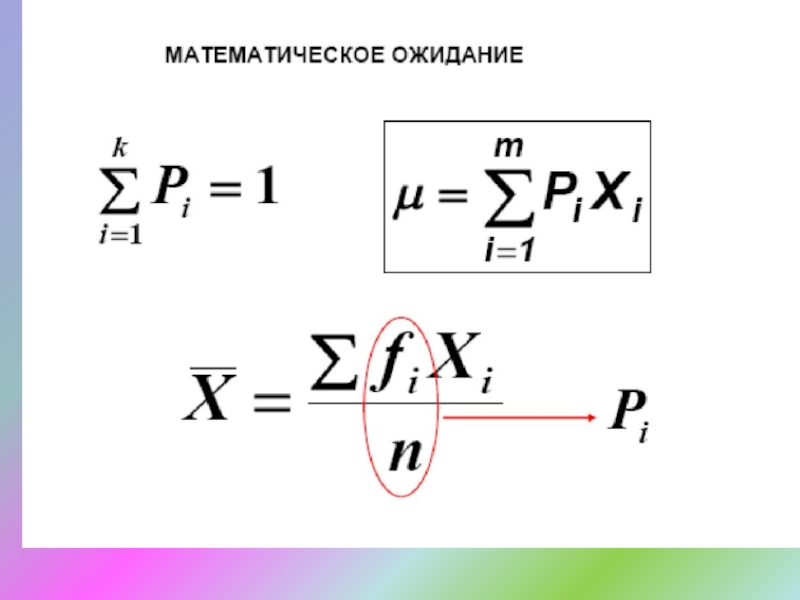Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы био-статистики
Содержание
- 1. Основы био-статистики
- 2. СТАТИСТИКА – самостоятельная общественная наука, изучающая количественную
- 3. Медицинская статистика является отраслевой статистикой, которая изучает
- 4. Методы сбора информации, ее изучения, обработки и
- 5. Основные разделы медицинской статистики:Статистика здоровья населения,Статистика здравоохранения.
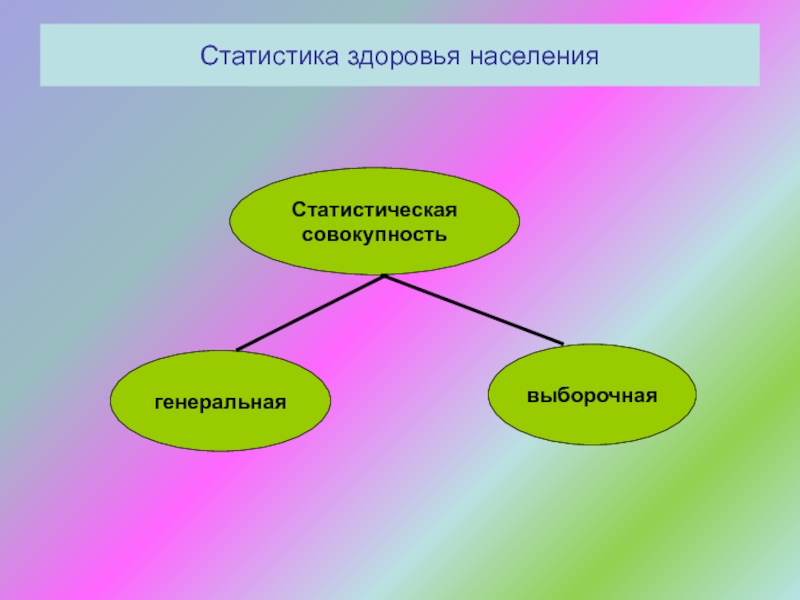
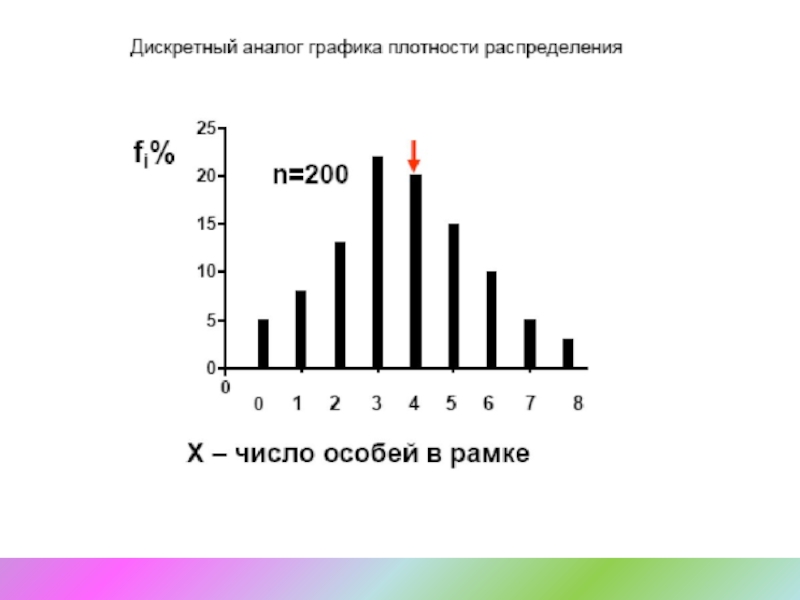
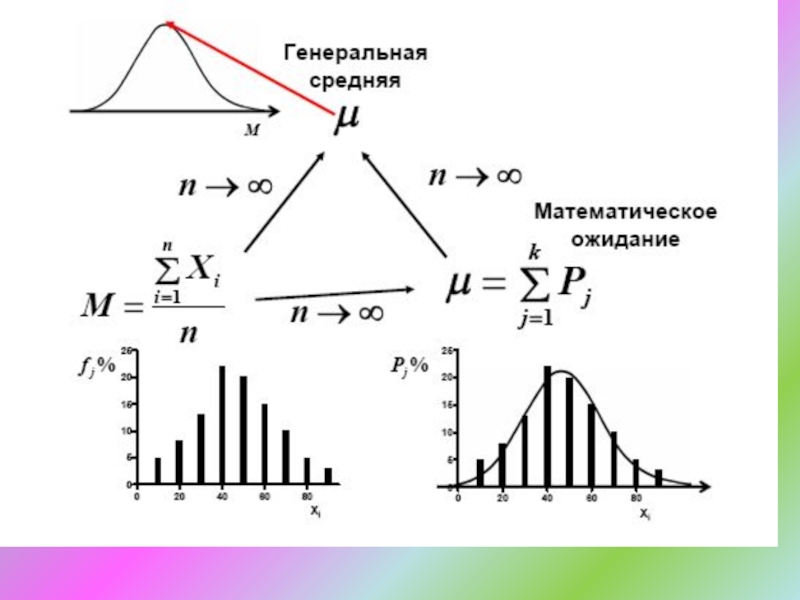
- 6. Статистика здоровья населенияСтатистическая совокупность – группа, состоящая
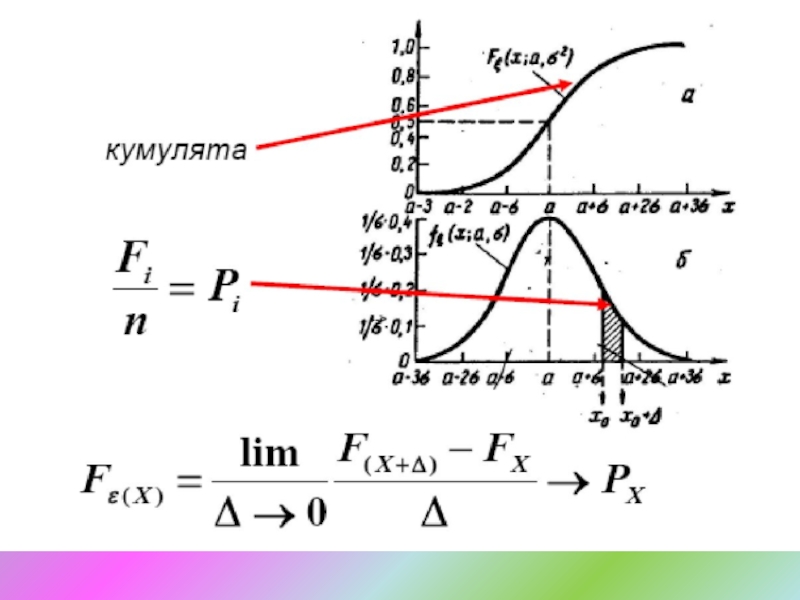
- 7. Статистика здоровья населенияСтатистическая совокупностьгенеральнаявыборочная
- 8. Статистика здоровья населенияГенеральная совокупность – совокупность
- 9. Статистика здоровья населенияВыборочная совокупность должна отражать структуру
- 10. Статистика здоровья населения Формула определения минимального объема
- 11. Статистика здоровья населения Бесповторный отбор единиц наблюдения:1.
- 12. Статистика здоровья населенияТочность исследования - приближение, с
- 13. Статистика здоровья населенияВиды относительных показателей:1. Интенсивный (частоты)2.
- 14. Статистика здоровья населения- распределительный Отношение между частями
- 15. Статистика здоровья населенияуказательный Уровень
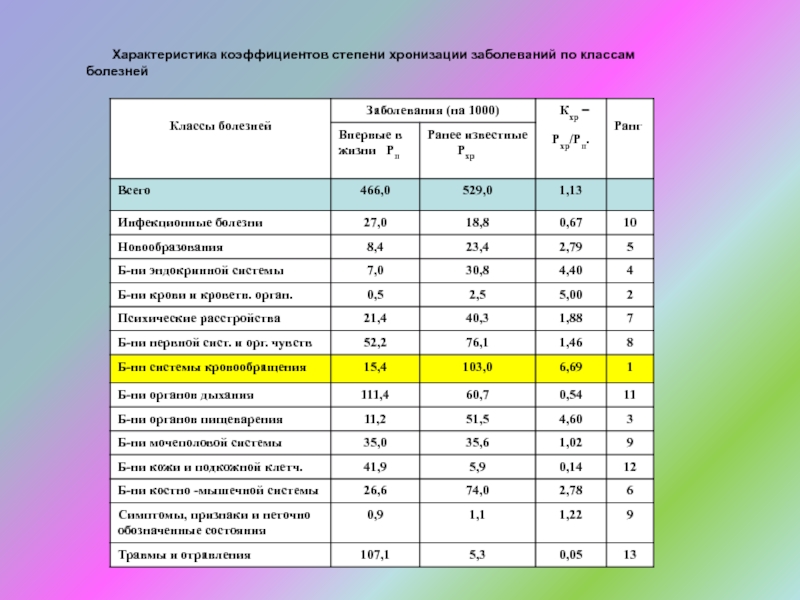
- 16. Характеристика коэффициентов степени хронизации заболеваний по классам болезней
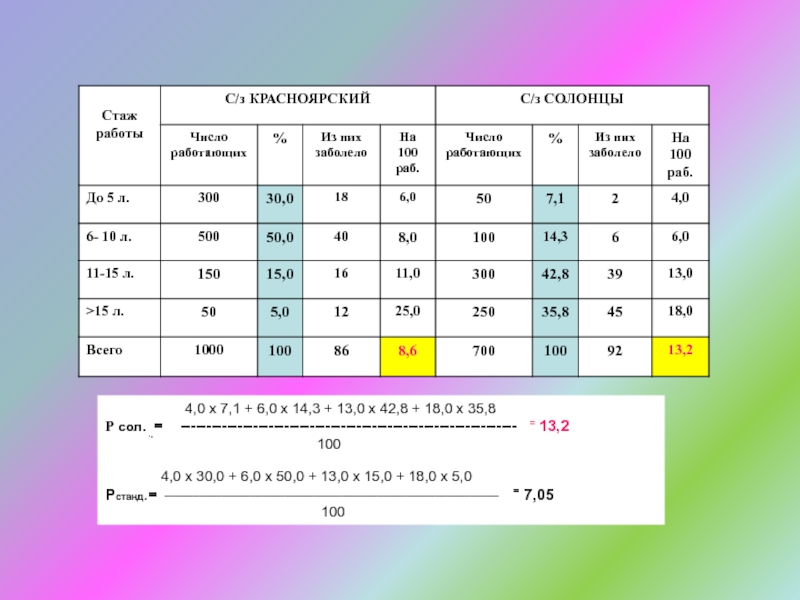
- 17. Статистика здоровья населенияОценка достоверности различий показателей__________________________________Задача: Провести
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Статистика здоровья населенияОбласти применения средних величин:в клинических
- 35. Повторение изученногоНайди среднее арифметическое чисел:А) 4,4,7Б) 10,5,5,8В) 250,50,100,100,500
- 36. Средние величины26,23,18,25,20,25,30,25,34,19.(26+23+18+25+20+25+30+25+34+19): 10 = 245:10 = 24,5
- 37. Число, наиболее часто встречающееся
- 38. Способы расчета средней арифметической Простая - М =
- 39. Основные критерии разнообразия признаковЛимит – это значения
- 40. Разнообразие26,23,18,25,20,25,30,25,34,19.Разница между наибольшим и наименьшим числом называется
- 41. Оценка достоверности результатов исследованияПогрешность средней величины:mM =
- 42. Оценка достоверности разницы относительных и средних величин
- 43. Динамический ряд - это ряд однородных статистических
- 44. Показатели динамического рядаАбсолютный прирост - разница между
- 45. Методы стандартизации показателейПрямойНепрямойОбратный Используются в случаях, когда нужно сравнить явление, которое изучается в неоднородной совокупности
- 46. Этапы прямого метода стандартизацииВычисление интенсивных показателейВыбор и
- 47. Корреляционный анализприменяется для определения взаимосвязи между явлениямиКорреляционная
- 48. Способы определения коэффициента корреляцииМетод рангов (Спирмена)Метод квадратов (Пирсона)
- 49. Оценка силы и характера корреляционной связи
- 50. Виды графических изображений Диаграммы Картограммы Картодиаграммы
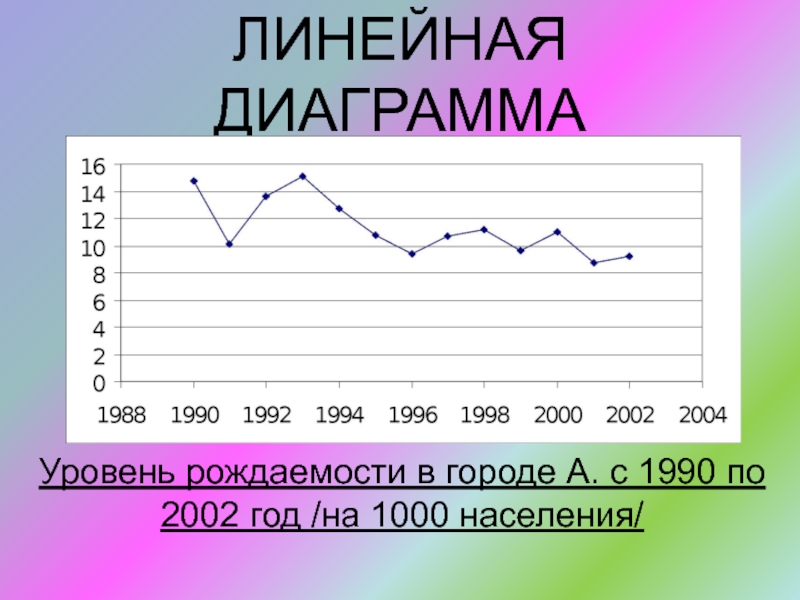
- 51. ЛИНЕЙНАЯ ДИАГРАММАУровень рождаемости в городе А. с 1990 по 2002 год /на 1000 населения/
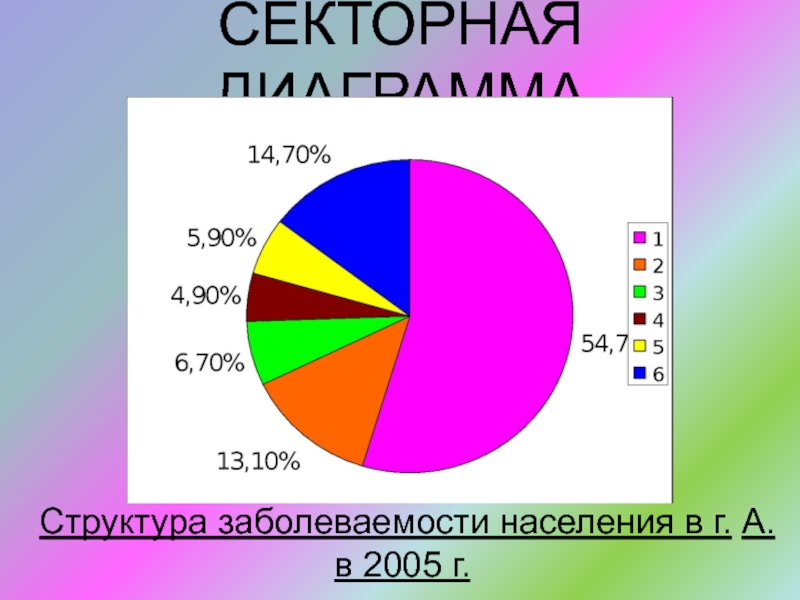
- 52. СЕКТОРНАЯ ДИАГРАММАСтруктура заболеваемости населения в г. А. в 2005 г.
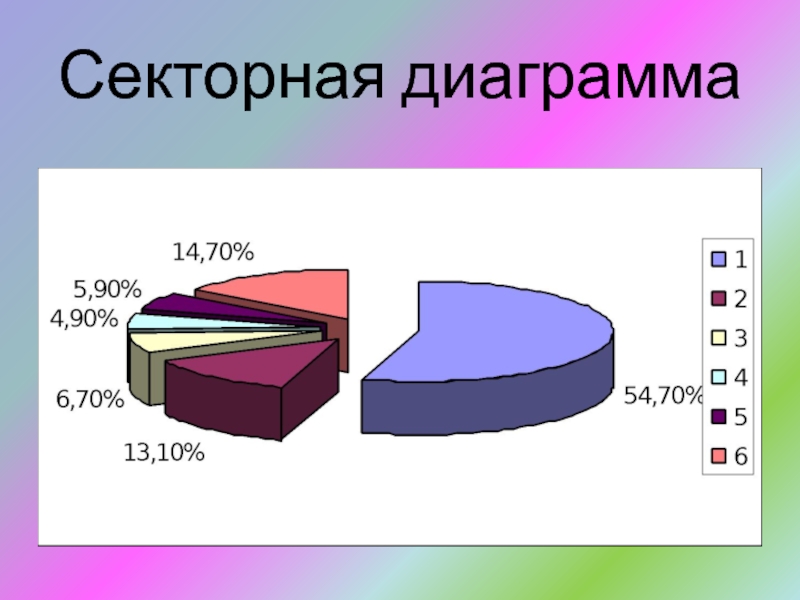
- 53. Секторная диаграмма
- 54. РАДИАЛЬНАЯ ДИАГРАММАЧисло случаев заболеваемости с временной потерей
- 55. Спасибо за внимание!
- 56. Скачать презентанцию
СТАТИСТИКА – самостоятельная общественная наука, изучающая количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной.
Слайды и текст этой презентации
Слайд 2
СТАТИСТИКА – самостоятельная общественная наука, изучающая количественную сторону массовых общественных
явлений в неразрывной связи с их качественной стороной.
Слайд 3Медицинская статистика является отраслевой статистикой, которая изучает вопросы, связанные с
медициной, как областью науки и практической деятельности, направленной на сохранение
и укрепление здоровья людей, предупреждение и лечение болезней.
Слайд 4
Методы сбора информации, ее изучения, обработки и анализа, имеющиеся в
арсенале медицинской статистики используются всеми клиническими и теоретическими дисциплинами нашей
отрасли.
Слайд 5
Основные разделы медицинской статистики:
Статистика здоровья населения,
Статистика здравоохранения.
Слайд 6Статистика здоровья населения
Статистическая совокупность –
группа, состоящая из определенного числа
относительно однородных элементов (единиц наблюдения), взятых вместе в конкретных границах
времени и пространства.
Слайд 8Статистика здоровья населения
Генеральная совокупность –
совокупность всех единиц
наблюдения в соответствии с целью исследования.
Выборочная совокупность – часть генеральной
совокупности, отобранная специальным методом и предназначенная для характеристики генеральной совокупности.
Слайд 9Статистика здоровья населения
Выборочная совокупность должна отражать структуру и свойства генеральной,
т.е. быть по отношению к ней представительной (репрезентативной).
Слайд 10Статистика здоровья населения
Формула определения минимального объема выборочной совокупности
t2 x
pq
n = ---------------
Δ2
Пример:
22 x 50,0 * 50,0n = --------------------------------- = 100
102
n – требуемое число наблюдений,
t – критерий достоверности,
p - показатель
распространенности,
q = 1 – p или (100 – p),
Δ – предельная ошибка.
Δ = t x m, где
m – ошибка показателя
Слайд 11Статистика здоровья населения
Бесповторный отбор единиц наблюдения:
1. Случайная выборка:
- метод
жеребьевки,
- метод случайных чисел
2. Механическая выборка
3. Типическая
(типологическая) выборка
4. Серийная выборка
Фрагмент
таблицы случайных чисел:
22268 33438 80072 15542 48690
89788 61740 98666 56241 65233
33302 48110 01135 79509 74652
03164 51354 41271 70338
91413 49689 65814 52444 83068
83024 15196 33225 53066 15830
41487 92226 99027 97751 54987
46768 34578 67195 13303 39784
05088 91708 18073 59685 50768
58476 78094 72652 38655 74018
67348 77768 79736 08602
Слайд 12Статистика здоровья населения
Точность исследования - приближение, с которым получаются подлинные
значения показателей.
__________________________________
Надежность исследования определяется вероятностью ошибки полученного показателя.
Ошибка показателя
P x qm = √ -------------- P ± m
n
______________________________
Достоверность показателя
P
t = -----≥ 2,0 (95,0%)
m
P ≥ 0,95 (95% достоверности)
p ≤ 0,05 (вероятность ошибки)
Слайд 13Статистика здоровья населения
Виды относительных показателей:
1. Интенсивный (частоты)
2. Экстенсивный:
- альтернативный,
Число умерших
за годСмертность = ----------------------------- х 1000
Среднегодовая
численность
населения
Отношение числа случаев, имеющих признак к числу всех случаев
Число больных
P = --------------------------------------------- х 1000
число здоровых + число больных
Статистика здоровья населения
Слайд 14Статистика здоровья населения
- распределительный
Отношение между частями и целым
Структура заболеваний
(в %)
Гипертоническая болезнь
- 30,0Ишемич. болезнь сердца - 20,0
Легочное сердце - 5,0
Другие болезни сердца - 7,0
Цереброваскулярные болезни - 15,0
Б-ни артерий, артериол, капил. - 5,0
Болезни вен и лимф. сосудов - 3,0
Др. б-ни системы кровообращения - 15,0
ВСЕГО…………………………………… 100,0
Слайд 15Статистика здоровья населения
указательный
Уровень обращаемости по ранее
извест. заб.
k = -------------------------------------------------
Уровень первичной заболеваемостиСоотношения
Отношение между частями целого
Гипертоническая болезнь 30,0
--------------------------------------------- = ------- = 2,0
Цереброваскулярные болезни 15,0
Соотношение двух независимых совокупностей
Количество коек
P = -------------------------------------- х 10 000
Численность населения
Слайд 17Статистика здоровья населения
Оценка достоверности различий показателей
__________________________________
Задача: Провести сравнительный анализ ЗВУТ
по двум совхозам (Солонцы и Красноярский)
С/з Красноярский: Из 1000 работающих
случаев забол. с ВУТ за год было 86. На 100 работающих - (86 х 100) : 1000 = 8,6
m = ± 0,9
С/з Солонцы: Из 700 работающих случаев забол. с ВУТ за год было 92.
На 100 работающих – (92 х 100) : 700 = 13,2
m = ± 1,3
P1 – P2
t = --------------- ≥ 2 (95,5%)
√ m12 + m22
Pq
m = √--------
n
____________________________________
13,2 – 8,6 4,6
t = --------------- = -------- = 2,9
√ 1,32 + 0,92 1,6
Вывод: ЗВУТ в с/з Солонцы существенно (достоверно) выше, чем в с/з Красноярский.
Вопрос: Чем это обусловлено?
Слайд 18
4,0 х 7,1 + 6,0 х 14,3 + 13,0 х
42,8 + 18,0 х 35,8Р сол. ..= ----------------------------------------------------------------- = 13,2
100
4,0 х 30,0 + 6,0 х 50,0 + 13,0 х 15,0 + 18,0 х 5,0
Рстанд.= __________________________________________________________ = 7,05
100
Слайд 34Статистика здоровья населения
Области применения средних величин:
в клинических и лабораторных исследованиях,
при
оценке физического развития населения,
при эпидемиологических и гигиенических обследованиях,
при оценке деятельности
медицинских учреждений.
Слайд 35Повторение изученного
Найди среднее арифметическое чисел:
А) 4,4,7
Б) 10,5,5,8
В) 250,50,100,100,500
Слайд 36Средние величины
26,23,18,25,20,25,30,25,34,19.
(26+23+18+25+20+25+30+25+34+19): 10 = 245:10 = 24,5
24,5
– среднее арифметическое
18 – наименьшее время
34 – наибольшее время 
Слайд 37 Число, наиболее часто встречающееся в данном ряду,
называется модой ряда чисел.
25 – мода ряда чисел.
Ряд может иметь две моды, а может не иметь моды. Например, 47,46,50,52,47,49,52,55 – имеет две моды: 47 и 52
59,68,66,70,67,71,74 – этот ряд не имеет моды.
Слайд 38Способы расчета средней арифметической
Простая - М =
Взвешенная - М
=
По способу моментов - М = А+ і
Слайд 39Основные критерии разнообразия признаков
Лимит – это значения крайних вариант в
вариационном ряде
lim =
Vmin ÷VmaxАмплитуда – это разница крайних вариант вариационного а
Am = Vmax – Vmin
Среднее квадратическое отклонение – характеризует рассеивание вариант вокруг средней величины (внутреннюю структуру совокупности).
σ = среднеарифметический способ
σ = i способ моментов
Слайд 40Разнообразие
26,23,18,25,20,25,30,25,34,19.
Разница между наибольшим и наименьшим числом называется размахом ряда чисел
(амплитудой).
34 -18 = 16, это амплитуда ряда чисел.
Слайд 41Оценка достоверности результатов исследования
Погрешность средней величины:
mM =
, если n > 30;
mM=
, если n ≤ 30.Погрешность относительной величины:
m% /или mp/= , если n>30;
m% /или mp/ = , если n≤30
Слайд 42Оценка достоверности разницы относительных и средних величин
t =
- для средних величин;
t = - для относительных величин
Разница достоверна при t = 2 и больше, что отвечает вероятности безошибочного прогноза Р = 95,5 % и больше.
Слайд 43Динамический ряд - это ряд однородных статистических величин, которые показывают
изменение какого-то явления во времени
Простой динамический ряд - выраженный абсолютными
величинами.Сложный динамический ряд - выраженный относительными и средними величинами
Слайд 44Показатели динамического ряда
Абсолютный прирост - разница между настоящим и предыдущим
уровнями ряда
Темп роста - отношение настоящего уровня к предыдущему уровню
(в %)Темп прироста - отношение абсолютного прироста к предыдущему уровню (в %)
Показатель наглядности
Слайд 45Методы стандартизации показателей
Прямой
Непрямой
Обратный
Используются в случаях, когда нужно сравнить явление, которое
изучается в неоднородной совокупности
Слайд 46Этапы прямого метода стандартизации
Вычисление интенсивных показателей
Выбор и вычисление стандарта
Вычисление “ожидаемых”
величин
Вычисление стандартизированных показателей
Сравнение простых интенсивных и стандартизированных показателей
Слайд 47Корреляционный анализ
применяется для определения взаимосвязи между явлениями
Корреляционная связь бывает:
по характеру
- прямой и обратной;
по силе: сильной, средней, слабой
Слайд 54РАДИАЛЬНАЯ ДИАГРАММА
Число случаев заболеваемости с временной потерей трудоспособности на 100
работающих на Н-ском комбайновом заводе в 2006 г.
