Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
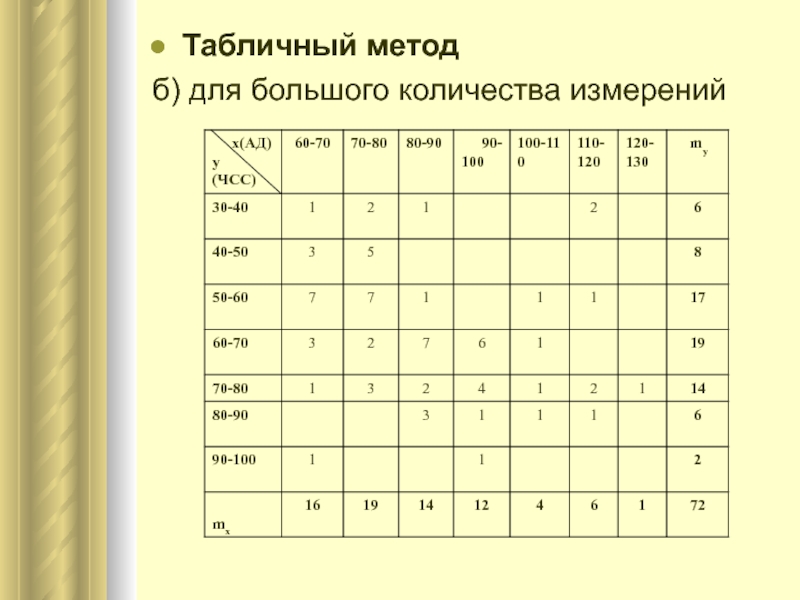
- Биология
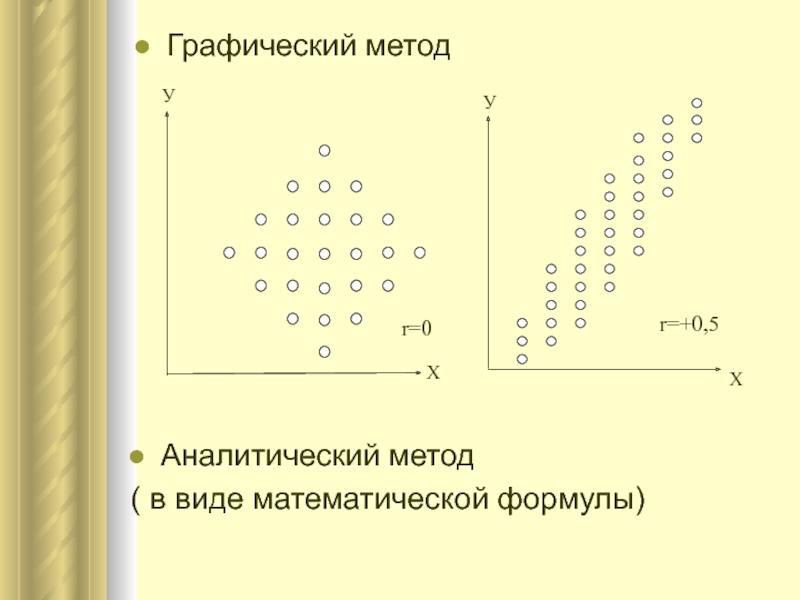
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы корреляционного анализа
Содержание
- 1. Основы корреляционного анализа
- 2. План лекции:Виды зависимостей и способы их представленияЗадачи корреляционного анализаКорреляция ранговКоэффициент ассоциации (тетрахорический показатель связи)
- 3. Виды зависимостей При функциональных зависимостях
- 4. Изучение корреляционных зависимостей Табличный метода) для небольшого количества измерений, не сгруппированных в классы
- 5. Табличный методб) для большого количества измерений
- 6. Графический методАналитический метод ( в виде математической формулы)УУХХr=0r=+0,5
- 7. ЗАДАЧИ КОРРЕЛЯЦИОННОГО АНАЛИЗА Определение тесноты (степени сопряженности)
- 8. Нахождение коэффициента корреляцииковариациядля выборки изn опытов
- 9. коэффициент корреляциитак как
- 10. Если r < 0,3 –
- 11. Слайд 11
- 12. r > 0,5 – связь значительнаяt0.95;20=2,1
- 13. КОРРЕЛЯЦИЯ РАНГОВ rp - коэффициент Спирмена для
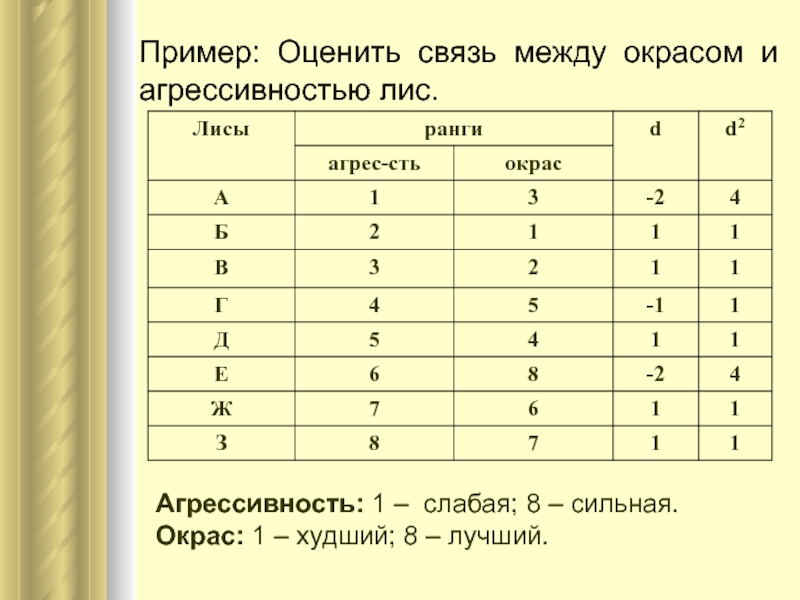
- 14. Пример: Оценить связь между окрасом и агрессивностью
- 15. Вывод: с вероятностью большей 0,95 можно сказать,
- 16. КОЭФФИЦИЕНТ АССОЦИАЦИИ (тетрахорический показатель связи) Используется, когда
- 17. ПРИМЕР: При проверке действия прививки против сыпного
- 18. Достоверность определяется по критерию χ2++=n·r2++=210·0,2052=8,83Для числа степеней
- 19. БЛАГОДАРЮ ЗА ВНИМАНИЕ
- 20. Скачать презентанцию
План лекции:Виды зависимостей и способы их представленияЗадачи корреляционного анализаКорреляция ранговКоэффициент ассоциации (тетрахорический показатель связи)
Слайды и текст этой презентации
Слайд 2План лекции:
Виды зависимостей и способы их представления
Задачи корреляционного анализа
Корреляция рангов
Коэффициент
ассоциации (тетрахорический показатель связи)
Слайд 3Виды зависимостей
При функциональных зависимостях каждому
значению одной переменной величины соответствует
одно вполне
определенное значение другой переменной (функции).
Корреляционные (статистические) связи
характеризуются тем, что численному
значению одной переменной соответствует много
значений (распределение) другой переменной.
Слайд 4Изучение корреляционных зависимостей
Табличный метод
а) для небольшого количества измерений, не
сгруппированных в классы
Слайд 7ЗАДАЧИ КОРРЕЛЯЦИОННОГО АНАЛИЗА
Определение тесноты (степени сопряженности) между варьируемыми признаками
Определение
формы и направления связи
КОРРЕЛЯЦИЯ бывает: положительной (прямой)
и отрицательной (обратной) По форме – линейной и нелинейной.
Слайд 10
Если
r < 0,3 – связь слабая;
0,3 ≤
r ≤ 0,5 – связь умеренная;
0,5 ≤ r ≤
0,7 – связь значительная;0,7 ≤ r ≤ 0,9 – связь сильная;
r = 0 – связь отсутствует;
r = 1 – связь функциональная.
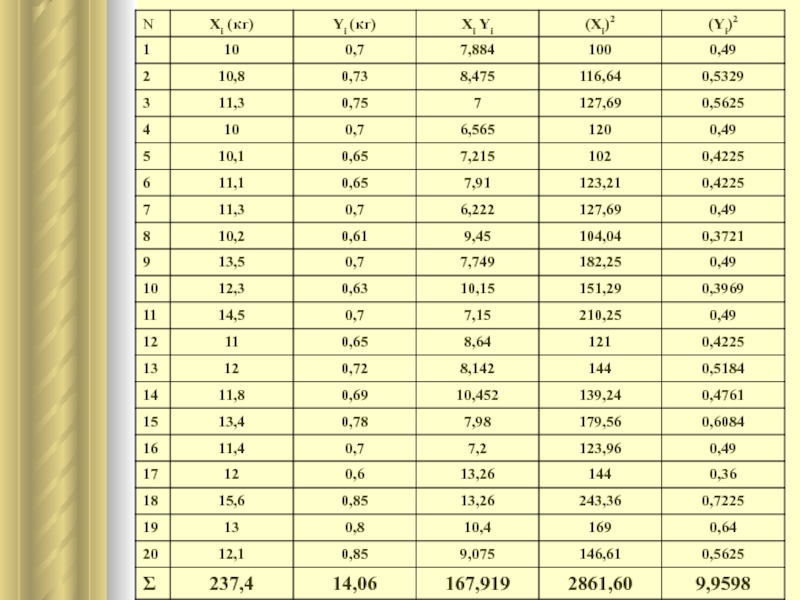
Пример: Определить наличие связи между весом обезьян и весом их детенышей. Оценить достоверность полученных результатов.
Слайд 12
r > 0,5 – связь значительная
t0.95;20=2,1
tэксп > tтабл
связь достоверна, т.е. между
весом матери и
весом детеныша существует прямая значительная связь.
Слайд 13КОРРЕЛЯЦИЯ РАНГОВ
rp - коэффициент Спирмена для непараметрических показателей.
d=xρ- yρ
; n – объем выборки.
Коэффициент достоверности (для
числа пар рангов больше 9):
Слайд 14Пример: Оценить связь между окрасом и агрессивностью лис.
Агрессивность: 1 –
слабая; 8 – сильная.
Окрас: 1 – худший; 8 – лучший.
Слайд 15
Вывод: с вероятностью большей 0,95 можно сказать, что между окрасом
лис и их агрессивностью существует прямая положительная связь
Слайд 16КОЭФФИЦИЕНТ АССОЦИАЦИИ
(тетрахорический показатель связи)
Используется, когда связь устанавливается только по
наличию или отсутствию признака.
a – особи, имеющие оба признака
(++);b – особи, имеющие первый признак, но не имеющие второго (+-);
c – особи, имеющие второй признак, но не имеющие первого (-+);
d – особи, не имеющие обоих признаков (--).
Слайд 17ПРИМЕР: При проверке действия прививки против сыпного тифа получены первичные
материалы о числе заболевших (-) и не заболевших (+) из
числа получивших (+) и не получивших (-) прививку. Оценить достоверность связи
Слайд 18Достоверность определяется по критерию χ2++=n·r2++=210·0,2052=8,83
Для числа степеней свободы ν=2-1 =1и
Р=0,95 табличное значение χ2++=3,8.
Т.е. связь между прививкой и не заболеванием
брюшным тифом прямая и достоверная.
