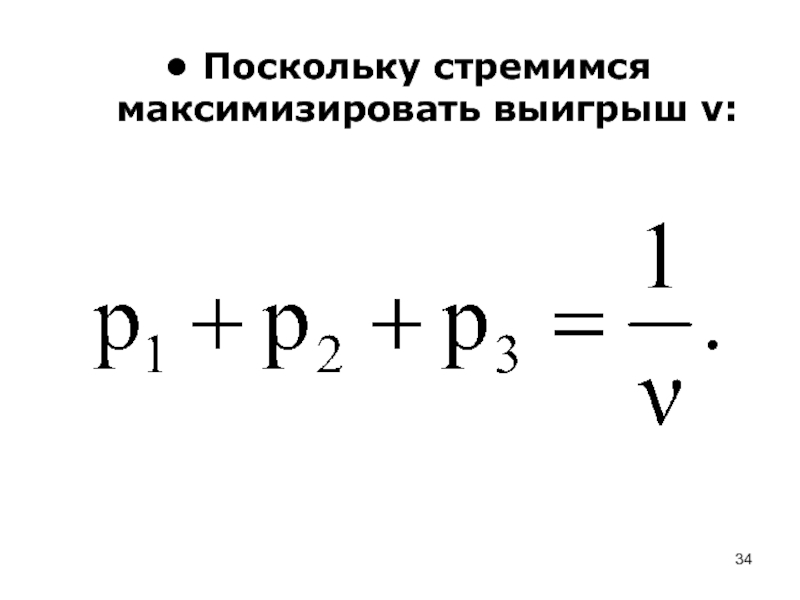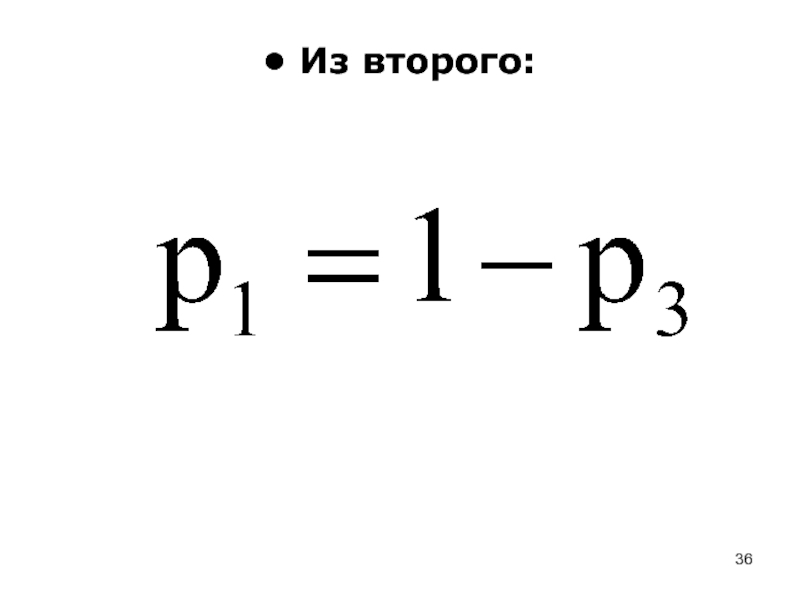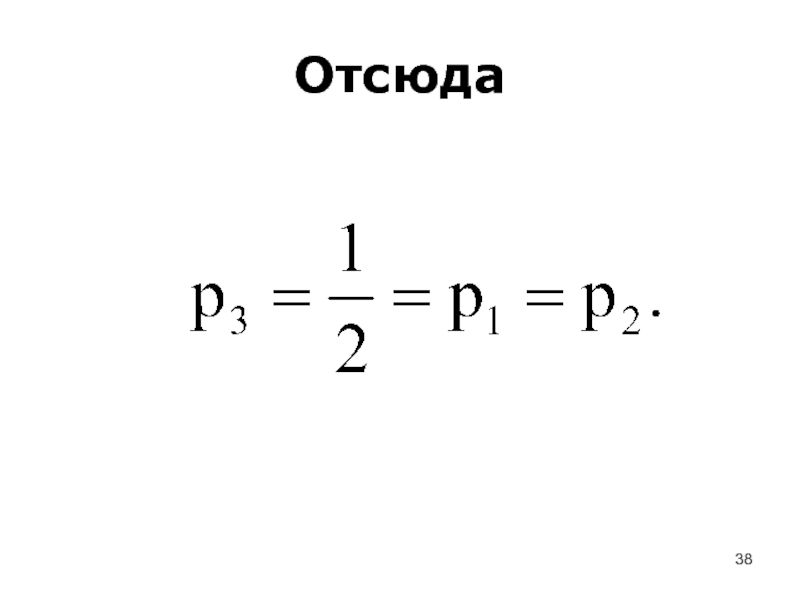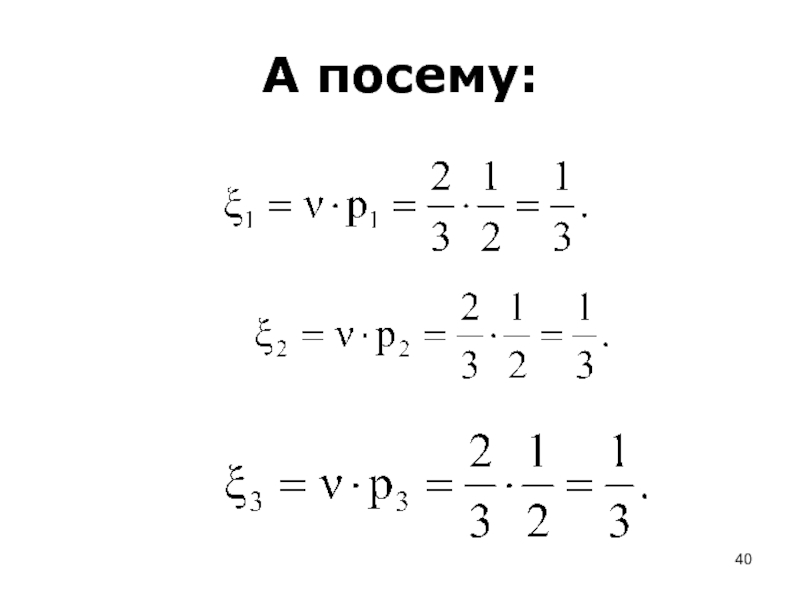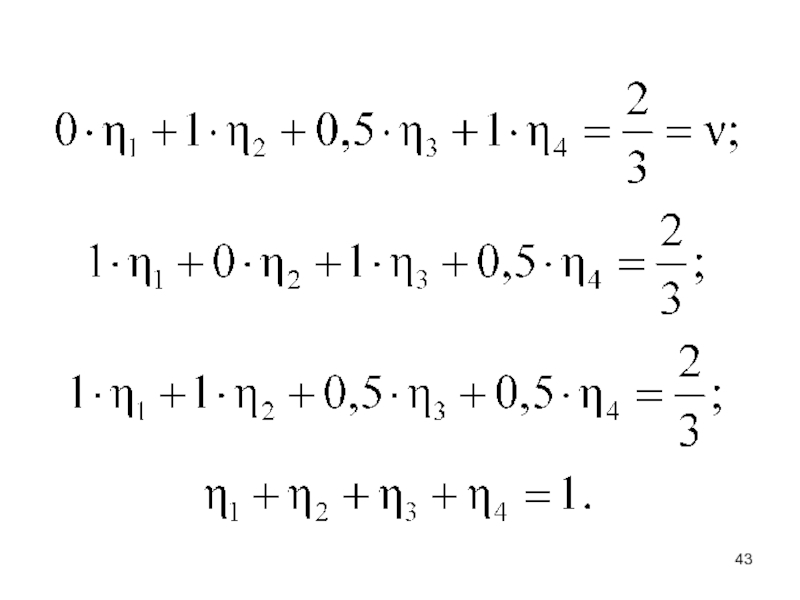Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории игр
Содержание
- 1. Основы теории игр
- 2. Другие примеры конфликтов – игры – шашки,
- 3. Далеко не каждый конфликт протекает по правилам
- 4. Таким образом, игра – это конфликт с чётко сформулированными условиями.
- 5. Часто результат игры даже при определённых стратегиях
- 6. Часто результат выражается числом, даже если это
- 7. Таким образом, основная задача теории игр формулируется
- 8. Парные игры. Если в конфликте участвуют две
- 9. Игры с нулевой суммой. Игра называется с
- 10. Конечные игры.Конечные игры – каждый игрок располагает
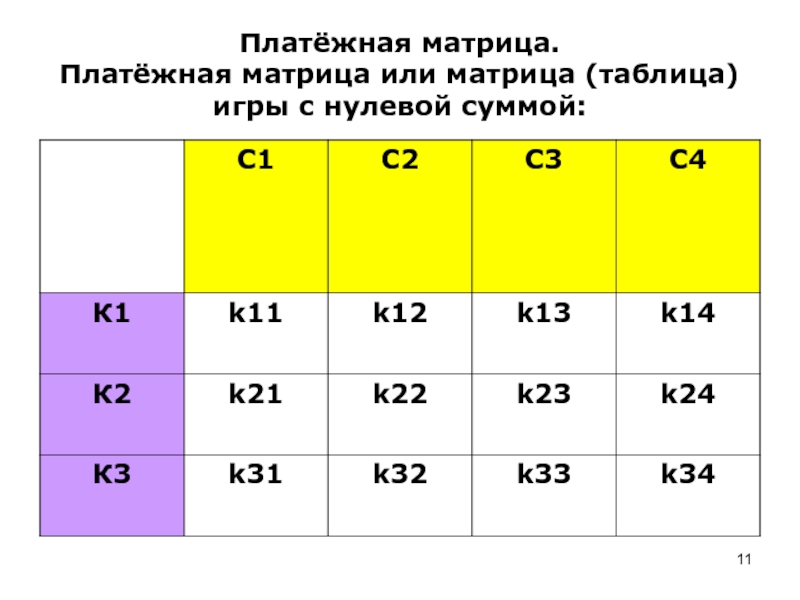
- 11. Платёжная матрица. Платёжная матрица или матрица (таблица) игры с нулевой суммой:
- 12. Здесь К «красный» игрок, С – «синий».
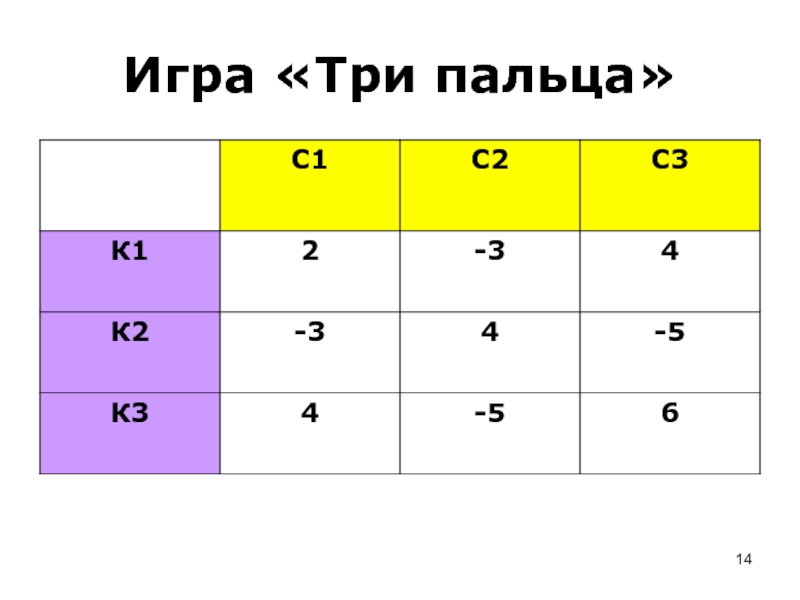
- 13. Игра «Три пальца» Два игрока К и
- 14. Игра «Три пальца»
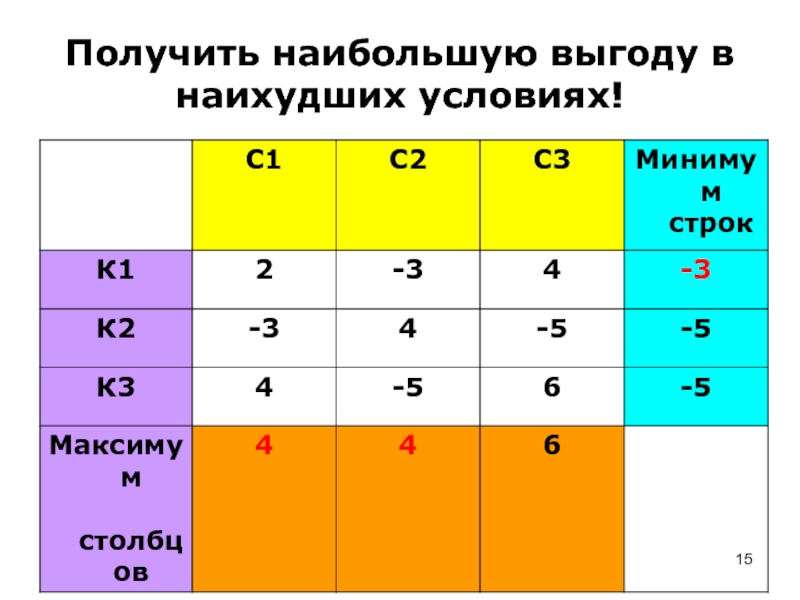
- 15. Получить наибольшую выгоду в наихудших условиях!
- 16. Нижняя цена игры – максимин α –
- 17. Это принцип минимакса и он является в
- 18. Пусть К показывает один палец (К1), а
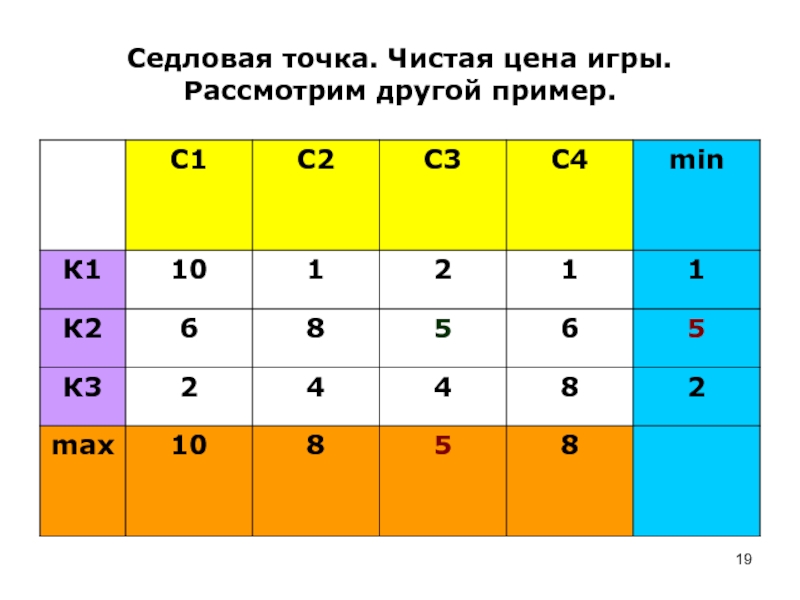
- 19. Седловая точка. Чистая цена игры. Рассмотрим другой пример.
- 20. Здесь α =5 и β =5. Особый
- 21. Если матрица игры имеет седловую точку (седловые
- 22. Систематическое применение этих стратегий, называемых оптимальными, обеспечивает
- 23. Если же одна из сторон от своей
- 24. Игра осада и оборона города «Красные» стремятся
- 25. Как должны действовать красные?Стратегии «красных» (дискретные):К1 –
- 26. Стратегии «синих» (дискретные):С1-поставить все три отряда на
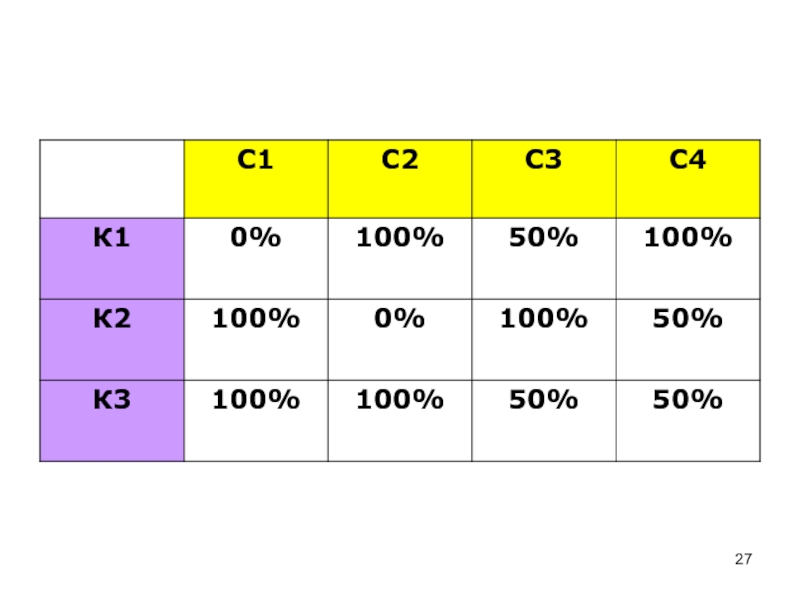
- 27. Слайд 27
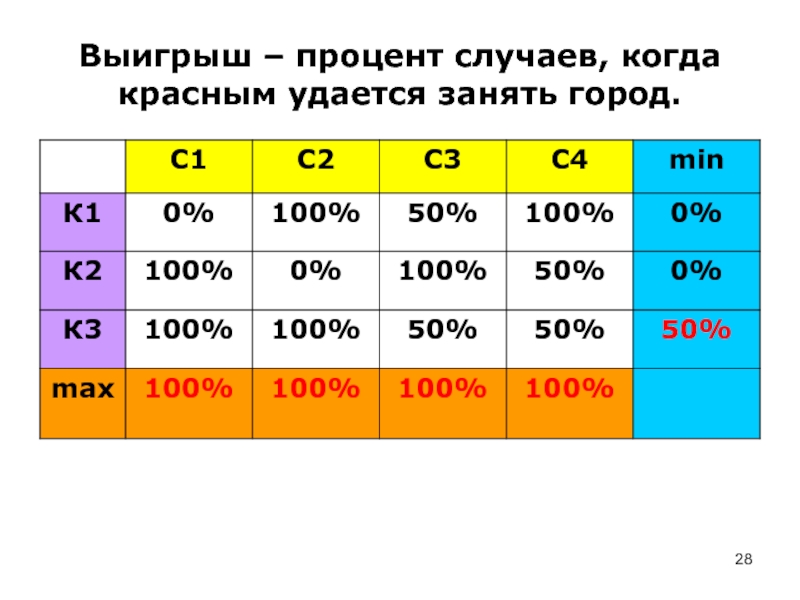
- 28. Выигрыш – процент случаев, когда красным удается занять город.
- 29. Таким образом, нижняя чистая цена игры α=50%,
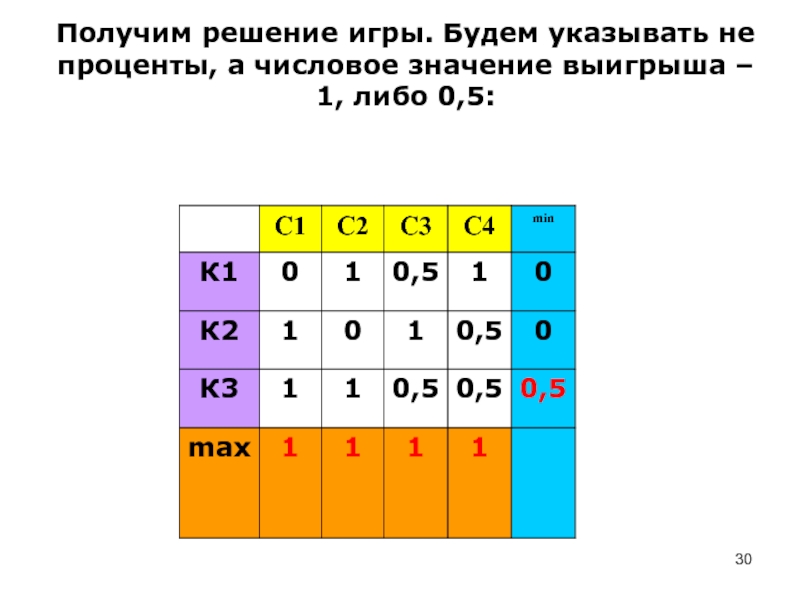
- 30. Получим решение игры. Будем указывать не
- 31. Составим систему уравнений для неизвестных значений оптимальной стратегии красных:
- 32. Разделим левые и правые части неравенств на значение правой части:
- 33. Обозначим и введём переменную z для перехода к равенствам:Тогда:
- 34. Поскольку стремимся максимизировать выигрыш ν:
- 35. Получили задачу линейного программирования.При полезных стратегиях синих получаем zi =0.Тогда из первого уравнения
- 36. Из второго:
- 37. Из третьего находим:
- 38. Отсюда
- 39. Тогда
- 40. А посему:
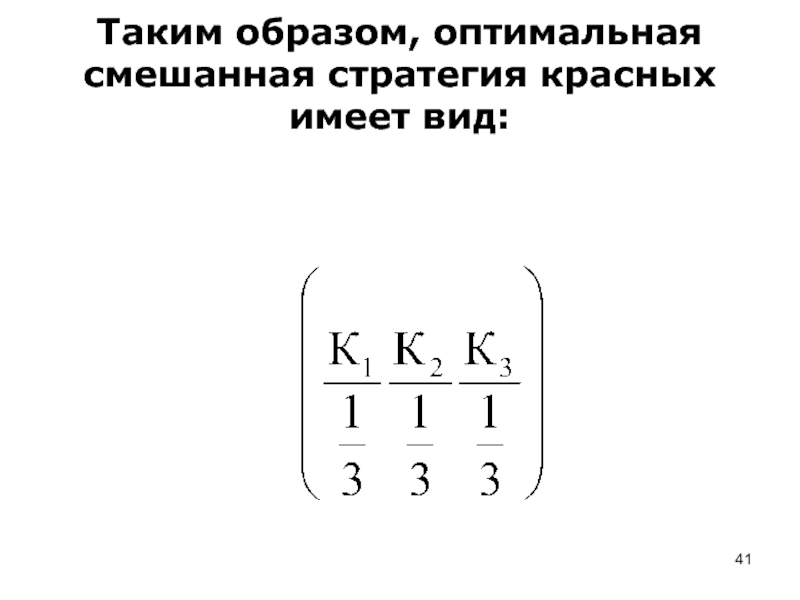
- 41. Таким образом, оптимальная смешанная стратегия красных имеет вид:
- 42. То есть красные должны одинаково часто применять
- 43. Слайд 43
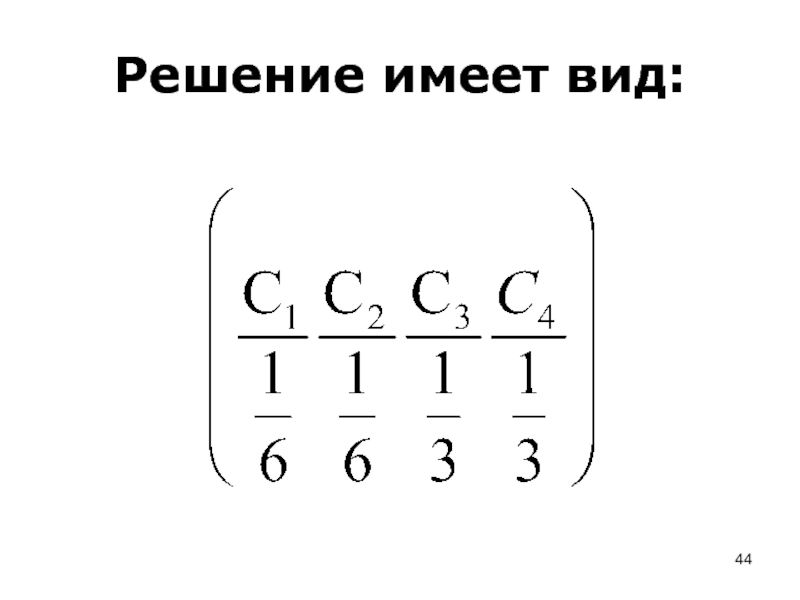
- 44. Решение имеет вид:
- 45. То есть синие в одной трети случаев
- 46. Скачать презентанцию
Другие примеры конфликтов – игры – шашки, шахматы, спортивные игры. Они отличаются тем, что ведутся по определённым правилам: перечень возможных ходов и к какому результату приводит некоторая совокупность ходов.
Слайды и текст этой презентации
Слайд 2Другие примеры конфликтов – игры – шашки, шахматы, спортивные игры.
Они отличаются тем, что ведутся по определённым правилам: перечень возможных
ходов и к какому результату приводит некоторая совокупность ходов.Слайд 3Далеко не каждый конфликт протекает по правилам («бои без правил»,
«русские воюют не по правилам»…).
Для математического анализа конфликта необходимо
представить конфликт в игровой форме, то есть указать стратегии (возможные действия) и уточнить, к какому результату приведёт игра, если каждый игрок выберет определённую стратегию. Слайд 5 Часто результат игры даже при определённых стратегиях предсказать невозможно, так
как всё зависит от случая.
Тогда говорят о среднем результате,
то есть о результате, приходящемся в среднем на одну партию, если будет сыграно достаточно большое число партий. То есть, даже если случайно «везёт», в среднем выигрывает тот, кто ведёт себя разумно.
Слайд 6Часто результат выражается числом, даже если это просто выигрыш (1),
либо проигрыш (0).
Мы будем полагать, что выигрыш (проигрыш) каждого
игрока выражается числом.Слайд 7Таким образом, основная задача теории игр формулируется так: как должен
вести себя (какую стратегию применять) разумный игрок в конфликте с
разумным противником (противниками), чтобы обеспечить себе в среднем наибольший возможный выигрыш?Слайд 8Парные игры.
Если в конфликте участвуют две стороны, то игра называется
парной, если несколько – множественной.
Мы ограничимся парными играми.
Слайд 9Игры с нулевой суммой.
Игра называется с нулевой суммой, если одна
сторона выигрывает то, что проигрывает другая.
Иногда называют – антагонистическая
игра. Это не всегда соблюдается. Например, один выигрывает одну сумму, а другой в этой же ситуации проигрывает другую.
Однако, во многих случаях парные игры с нулевой суммой не слишком искажают суть явлений.
Слайд 10Конечные игры.
Конечные игры – каждый игрок располагает конечным числом стратегий.
В этом, помимо всего прочего выражается своего рода дискретность игры.
Слайд 12Здесь К «красный» игрок, С – «синий».
У красного три
стратегии, у синего – четыре.
kij – выигрыш (проигрыш) красного, то
есть проигрыш(выигрыш) синего.Если игра представлена в виде такой таблицы (матрицы), то говорят, что игра приведена к нормальной форме.
Реально – как записать шахматы в нормальной форме?!
Слайд 13Игра «Три пальца»
Два игрока К и С одновременно и не
сговариваясь показывают один, два или три пальца.
Если всего показанных пальцев
( у К и С) будет чётное число, то выигрывает К – он получает столько очков, сколько показанных пальцев. Если всего показанных пальцев ( у К и С) будет нечётное число, то выигрывает С.
Запишем игру в нормальной форме.
Слайд 16Нижняя цена игры – максимин α – максимальный элемент среди
минимумов строк.
Верхняя цена игры – минимакс β – минимальный элемент
среди максимумов столбцов.Слайд 17Это принцип минимакса и он является в теории игр основным.
То есть вести себя так, чтобы получить наибольшую выгоду в
наихудших условиях. Значит, К целесообразно показывать один палец, а С – либо один, либо два.
Найденные нами стратегии обладают нехорошим свойством – они неустойчивы.
Слайд 18Пусть К показывает один палец (К1), а С – тоже
один(С1). К всегда выигрывает 2 очка.
Тогда С переходит на
С2 и будет выигрывать 3 очка. Тогда К, не будь дурак, переходит на К2. А С в ответ – на С3 и так далее…
Равновесии нарушается.
Слайд 20Здесь α =5 и β =5. Особый случай!
Пара стратегий К2,
С3 устойчива и представляет собой решение игры. Никому не выгодно
отступать от своих стратегий.Это связано с тем, что в матрице есть элемент, являющийся одновременно и минимаксом и максимином.
Такой элемент называется седловой точкой.
Сама седловая точка - цена игры.
Слайд 21Если матрица игры имеет седловую точку (седловые точки), то игра
имеет решение в так называемых чистых стратегиях.
Это пара стратегий,
пересекающихся в седловой точке.А если α не равно β ?
Решение есть и в этом случае, только оно лежит в области смешанных стратегий, то есть путём чередования стратегий с какими - то вероятностями.
Слайд 22Систематическое применение этих стратегий, называемых оптимальными, обеспечивает каждой стороне максимально
возможный для неё выигрыш, определяемый ценой игры.
Слайд 23Если же одна из сторон от своей оптимальной стратегии (в
то время как другая продолжает придерживаться своей), то это ни
в коем случае не может быть выгодно: выигрыш либо будет неизменным, либо уменьшится.Таки образом, каждая конечная игра имеет решение (возможно в области смешанных стратегий).
Это утверждает основная теорема теории игр.
Слайд 24Игра осада и оборона города
«Красные» стремятся занять город, «синие» обороняют.
В
город ведут две дороги 1 и 2.
У «красных» два отряда.
У «синих» - три отряда. Если встречаются равные силы «красных» и «синих», то в 50% случаях красные побеждают и занимают город, а в 50% случаев отступают.
Если красные встречаются с превосходящими силами синих ( один отряд на два или два с тремя) они отступают.
Слайд 25Как должны действовать красные?
Стратегии «красных» (дискретные):
К1 – послать оба отряда
по дороге 1;
К2 – послать оба отряда по дороге2;
К3 –
послать по одному отряду на каждую дорогу.Слайд 26Стратегии «синих» (дискретные):
С1-поставить все три отряда на дорогу 1;
С2-поставить все
три отряда на дорогу 2;
С3-поставить два отряда на дорогу 1
и один на дорогу 2;С4-поставить два отряда на дорогу 2 и один на дорогу 1.
Нет «одноотрядных» стратегий!
Слайд 29Таким образом, нижняя чистая цена игры α=50%, верхняя чистая цена
игры β=100%.
Тогда цена игры при смешанных стратегиях:
Слайд 30 Получим решение игры. Будем указывать не проценты, а числовое значение
выигрыша – 1, либо 0,5:
Слайд 35Получили задачу линейного программирования.
При полезных стратегиях синих получаем zi =0.
Тогда
из первого уравнения
Слайд 42То есть красные должны одинаково часто применять каждую из своих
стратегий.
Составим теперь систему уравнений для неизвестных значений оптимальной стратегии синих:
Слайд 45То есть синие в одной трети случаев посылают все три
отряда на одну дорогу (любую), а в остальных – две
на одну, а один – на другую.Однако, все эти рассуждения ориентированы на многократное проведение «экспериментов» - сражений.
Реальный бой реализуется один раз и кто выиграет определяется не теорией игр, а военным искусством…
На то оно и искусство!