Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории массового обслуживания
Содержание
- 1. Основы теории массового обслуживания
- 2. План лекции
- 3. Система массового обслуживания (СМО), как правило, состоит
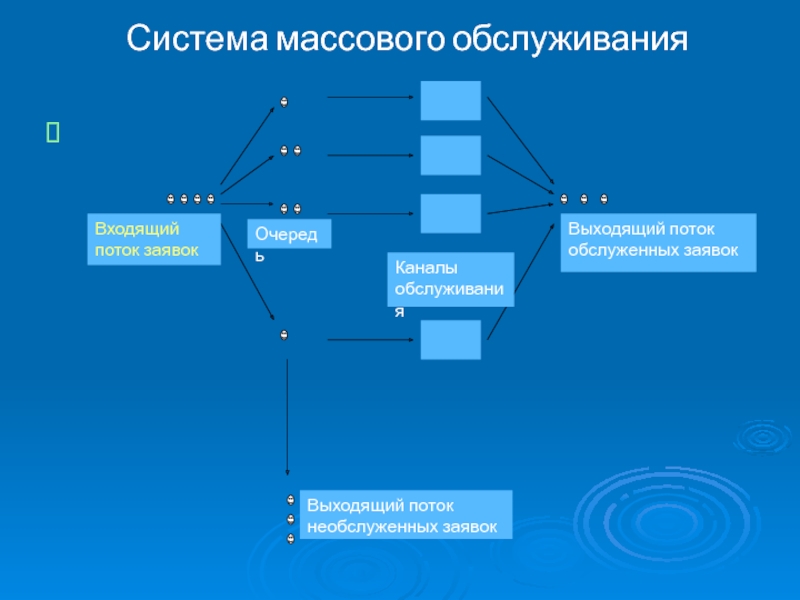
- 4. Система массового обслуживания
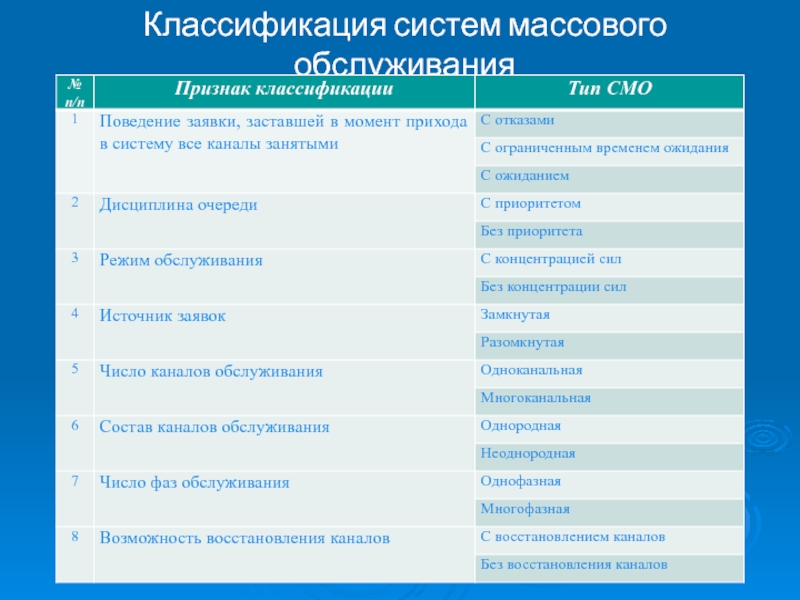
- 5. Классификация систем массового обслуживания
- 6. СМО с отказамиНа вход системы, состоящей из
- 7. Размеченный граф состояния СМО с отказамиλλλλλλμ2μ3μkμ(k+1)μnμ
- 8. СМО с отказамиВероятность того, что система находится
- 9. СМО с отказамиЕсли все каналы обслуживания заняты,
- 10. СМО с ограниченным временем ожиданияНа вход системы,
- 11. СМО с ограниченным временем ожиданияПараметр β называется
- 12. СМО с ожиданиемОсобенностью функционирования систем данного типа
- 13. СМО с ожиданиемВероятность того, что система находится
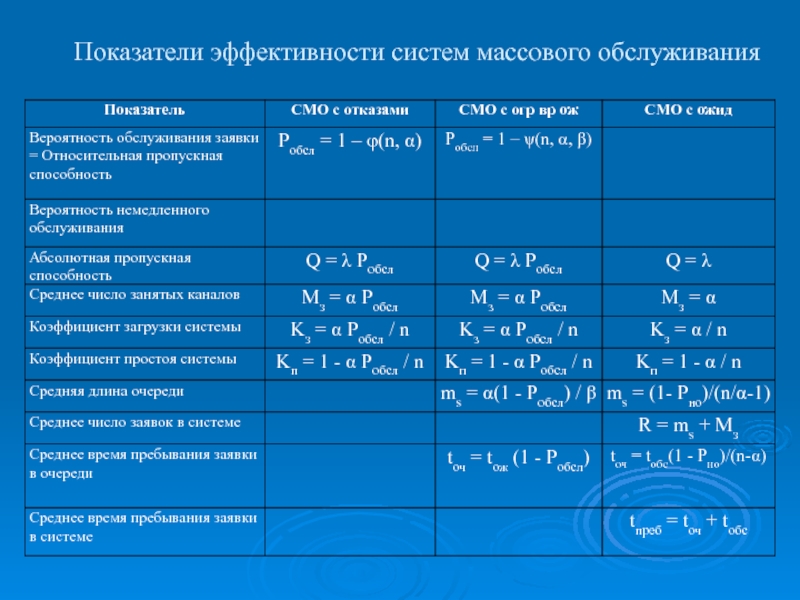
- 14. Показатели эффективности систем массового обслуживания
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Система массового обслуживания (СМО), как правило, состоит из следующих элементов:
Входящий
поток заявок
необслуженных заявокСлайд 6СМО с отказами
На вход системы, состоящей из n каналов обслуживания,
поступает простейший поток заявок с плотностью λ. На обслуживание каждой
заявки назначается один канал из числа свободных. Время обслуживания заявки случайно и подчиняется показательному закону распределения с параметром μ. Заявка, заставшая в момент поступления все каналы занятыми, получает отказ в обслуживании и покидает систему.Слайд 8СМО с отказами
Вероятность того, что система находится в состоянии Хк,
то есть, что в системе находится k заявок и, соответственно,
k каналов заняты, вычисляется по формуле Эрланга:Параметр α называется приведенной плотностью входящего потока заявок и представляет собой среднее число заявок, поступивших в систему за среднее время обслуживания одной заявки.
Слайд 9СМО с отказами
Если все каналы обслуживания заняты, т.е. k =
n, то очередная заявка получит отказ, вероятность отказа вычисляется по
формуле:Вероятность обслуживания как вероятность противоположного события рассчитывается по формуле: Pобс = 1 – Pотк = 1 – φ(n, α) = q.
Слайд 10СМО с ограниченным временем ожидания
На вход системы, состоящей из n
каналов обслуживания, поступает простейший поток заявок с плотностью λ. На
обслуживание каждой заявки назначается один канал из числа свободных. Время обслуживания заявки случайно и подчиняется показательному закону распределения с параметром μ. Заявка, заставшая в момент поступления все каналы занятыми, становится в очередь и ожидает обслуживания в течение случайного времени, распределенного по показательному закону с параметром ν. Если за время ожидания обслуживание не началось (ни один канал не освободился), то заявка покидает систему необслуженной; но если обслуживание началось, то оно доводится до конца независимо от времени пребывания заявки в очереди.Слайд 11СМО с ограниченным временем ожидания
Параметр β называется приведенной плотностью уходов
заявок из очереди необслуженными и представляет собой среднее число заявок,
уходящих из очереди необслуженными за среднее время обслуживания одной заявки, при условии, что в очереди в среднем одна заявка.Слайд 12СМО с ожиданием
Особенностью функционирования систем данного типа по сравнению со
СМО с ограниченным временем ожидания является то, что заявка, заставшая
в момент поступления все каналы занятыми, становится в очередь и ожидает обслуживания до тех пор, пока не освободится какой-либо канал. То есть, в СМО с ожиданием обслуживаются все заявки, и поток заявок, уходящих из очереди необслуженными отсутствует (ν = 0).Слайд 13СМО с ожиданием
Вероятность того, что система находится в состоянии Хn+s,
то есть, что в системе находится n+s заявок и, соответственно,
n каналов заняты и, кроме того, s заявок стоят в очереди, вычисляется по формуле Эрланга:Условием существования в системе установившегося режима является α < n, то есть, среднее число заявок, поступающих в систему за среднее время обслуживания одной заявки не должно превышать количества каналов в системе.