Основы теории сигналов

“знак”.
Сигнал − это материальный носитель информации. В природе он

проявляется в виде некоторого физического процесса.
Теория сигналов абстрагируется (отходит) от физической природы сигнала. Здесь оперируют математическими моделями сигналов.








С математической точки зрения сигнал представляет собой функцию, т.е. зависимость одной величины от другой, независимой переменной. По содержанию это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а целью обработки сигналов можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко - полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования.
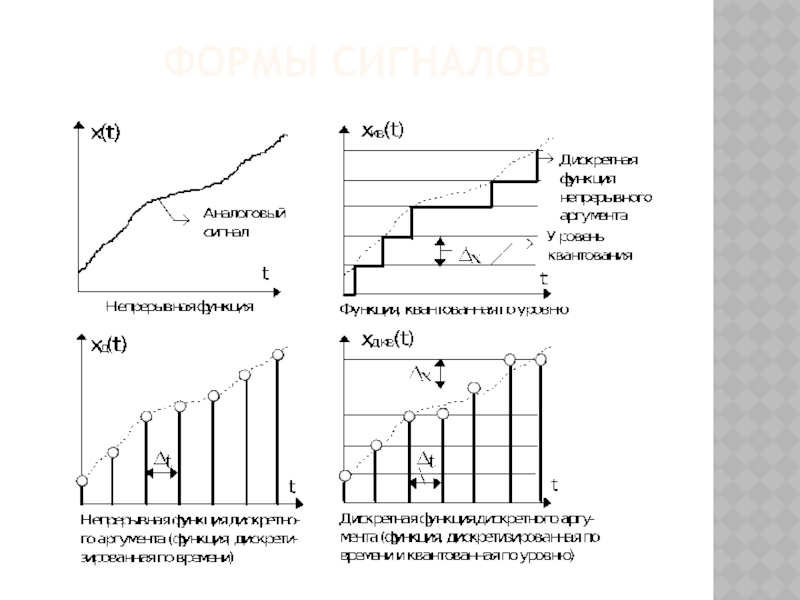
Обычно сигнал, независимо от его физической природы, представляют как некоторую функцию времени x(t). Такое представление есть общепринятая математическая абстракция физического сигнала.
Целями анализа сигналов обычно являются:
- Определение или оценка числовых параметров сигналов (энергия, средняя мощность, среднее квадратическое значение и пр.).
- Разложение сигналов на элементарные составляющие для сравнения свойств различных сигналов.
- Сравнение степени близости, "похожести", "родственности" различных сигналов, в том числе с определенными количественными оценками.

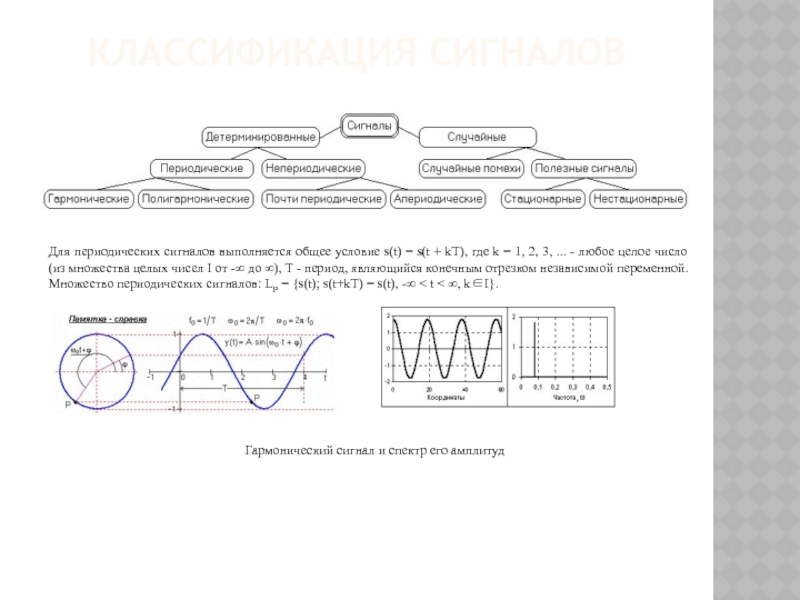
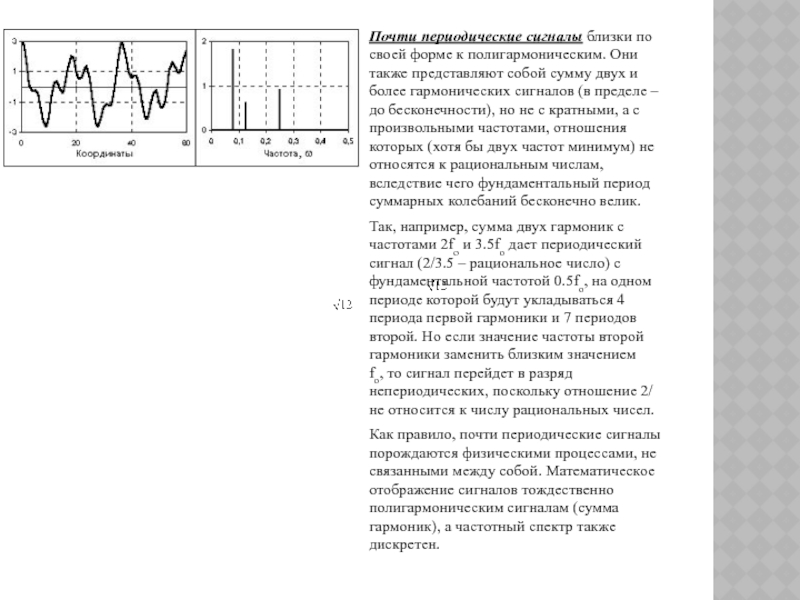
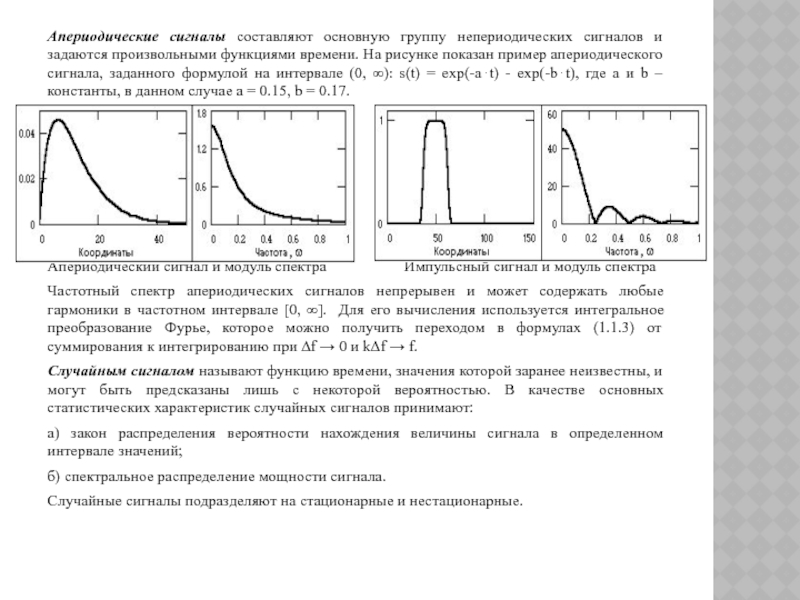
Все модели сигнала делятся на полные и неполные. Примерами полных моделей могут служить: функция времени x(t) и спектральная функция F(jω).
Полная модель отражает всю необходимую информацию о физическом сигнале.
Неполная модель (или оценка) дает не всю информацию о сигнале. Она позволяет описать его с некоторой погрешностью. В результате часть информации теряется.
Примерами неполных моделей могут служить: амплитудный спектр A(ω), энергетический спектр E(ω), корреляционная функция R(τ), набор дискретных значений некоторой функции .

энергетическому спектру, по характеру воздействия на сигнал, по вероятностным характеристикам

и другим признакам.
Источники помех бывают внутренние и внешние.
Электрические и магнитные поля различных источников помех вследствие наличия индуктивных, емкостных и резистивных связей создают на различных участках и цепях сигнальных систем паразитные разности потенциалов и токи, накладывающиеся на полезные сигналы.
Помехи подразделяются на флюктуационные, импульсные и периодические.
В зависимости от характера воздействия на сигнал помехи разделяют на аддитивные и мультипликативные.

по зависимости от времени (постоянные и переменные);
3) по элементу случайности

Детерминированный, или регулярный − это сигнал, закон изменения которого известен и известны все его параметры.
Квазидетерминированный − это сигнал, закон изменения которого известен, но один или несколько параметров − случайные величины. Пример: x(t)=Asin(wt+ϕ), где А − случайная величина.
Случайным называют сигнал, значение которого в каждый момент времени есть случайная величина. Кроме этого все сигналы могут быть непрерывными и дискретными.
Дискретизированным называют сигнал, у которого хотя бы один параметр является дискретной величиной, т.е. имеет конечное множество значений.

+ kT), где k = 1, 2, 3, ... -

любое целое число (из множества целых чисел I от -∞ до ∞), Т - период, являющийся конечным отрезком независимой переменной. Множество периодических сигналов: LP = {s(t); s(t+kT) = s(t), -∞ < t < ∞, k∈I}.

A⋅sin (wоt+φ),
s(t) = A⋅cos(wоt+j),

(1.1.1)
где А, fo, wo, j, φ - постоянные величины, которые могут исполнять роль информационных параметров сигнала: А - амплитуда сигнала, fо - циклическая частота в герцах, wо = 2pfо - угловая частота в радианах, j и φ- начальные фазовые углы в радианах. Период одного колебания T = 1/fо = 2p/wo. При ϕ = φ-π/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты fо (при t = 0).

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:
s(t) = An sin (2pfnt+jn), (1.1.2)

или непосредственно функцией s(t) = y(t ± kTp), k = 1,2,3,..., где Тр - период одного полного колебания сигнала y(t), заданного на одном периоде. Значение fp =1/Tp называют фундаментальной частотой колебаний.

Математическое описание сигнала задается формулой:

где: Ak = {5, 3, 4, 7} - амплитуда гармоник; fk = {0, 40, 80, 120} - частота в герцах; jk = {0, -0.4, -0.6, -0.8} - начальный фазовый угол колебаний в радианах; k = 0, 1, 2, 3. Фундаментальная частота сигнала 40 Гц.

Частотное представление данного сигнала (спектр сигнала) приведено на рисунке. Обратим внимание, что частотное представление периодического сигнала s(t), ограниченного по числу гармоник спектра, составляет всего восемь отсчетов и весьма компактно по сравнению с временным представлением.

суммы гармонических колебаний с частотами, кратными фундаментальной частоте колебаний fр

= 1/Тр. Для этого достаточно разложить один период сигнала в ряд Фурье по тригонометрическим функциям синуса и косинуса с шагом по частоте, равным фундаментальной частоте колебаний ∆f = fp: s(t) = (ak cos 2πk∆ft + bk sin 2πk∆ft), (1.1.3)
ao = (1/T) s(t) dt, ak = (2/T) s(t) cos 2πk∆ft dt (1.1.4)

bk = (2/T) s(t) sin 2πk∆ft dt (1.1.5)

Количество членов ряда Фурье K = kmax обычно ограничивается максимальными частотами fmax гармонических составляющих в сигналах так, чтобы fmax < K·fp. Однако для сигналов с разрывами и скачками имеет место fmax → ∞ , при этом количество членов ряда ограничивается по допустимой погрешности аппроксимации функции s(t).

Пример представления прямоугольного периодического сигнала (меандра) в виде амплитудного ряда Фурье в частотной области приведен на рисунке ниже. Сигнал четный относительно t=0, не имеет синусных гармоник, все значения jk для данной модели сигнала равны нулю.

Прямоугольный периодический сигнал (меандр)

также представляют собой сумму двух и более гармонических сигналов (в

пределе – до бесконечности), но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик.
Так, например, сумма двух гармоник с частотами 2fo и 3.5fo дает периодический сигнал (2/3.5 – рациональное число) с фундаментальной частотой 0.5fo, на одном периоде которой будут укладываться 4 периода первой гармоники и 7 периодов второй. Но если значение частоты второй гармоники заменить близким значением fo, то сигнал перейдет в разряд непериодических, поскольку отношение 2/ не относится к числу рациональных чисел.
Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.

функциями времени. На рисунке показан пример апериодического сигнала, заданного формулой

на интервале (0, ∞): s(t) = exp(-a⋅t) - exp(-b⋅t), где a и b – константы, в данном случае a = 0.15, b = 0.17.






Апериодический сигнал и модуль спектра Импульсный сигнал и модуль спектра
Частотный спектр апериодических сигналов непрерывен и может содержать любые гармоники в частотном интервале [0, ∞]. Для его вычисления используется интегральное преобразование Фурье, которое можно получить переходом в формулах (1.1.3) от суммирования к интегрированию при ∆f → 0 и k∆f → f.
Случайным сигналом называют функцию времени, значения которой заранее неизвестны, и могут быть предсказаны лишь с некоторой вероятностью. В качестве основных статистических характеристик случайных сигналов принимают:
а) закон распределения вероятности нахождения величины сигнала в определенном интервале значений;
б) спектральное распределение мощности сигнала.
Случайные сигналы подразделяют на стационарные и нестационарные.