Слайд 3Определение отношения
Бинарным отношением на множестве X называется всякое подмножество декартова
произведения X х X.
Так как в дальнейшем мы будем рассматривать
только бинарные отношения, то слово «бинарные», как правило, будем опускать.
Условимся отношения обозначать буквами R, S, Т, Р и др.
Слайд 4Обозначения
Если R - отношения на множестве X, то, согласно определению,
R X х X. С другой стороны, если задано некоторое подмножество
множества X х X, то оно определяет на множестве X некоторое отношение R.
Утверждение о том, что элементы х и у находятся в отношении R, можно записывать так: (x,y) R или x R y. Последняя запись читается: «Элемент х находится в отношении R с элементом у».
Слайд 5Пример (граф отношения)
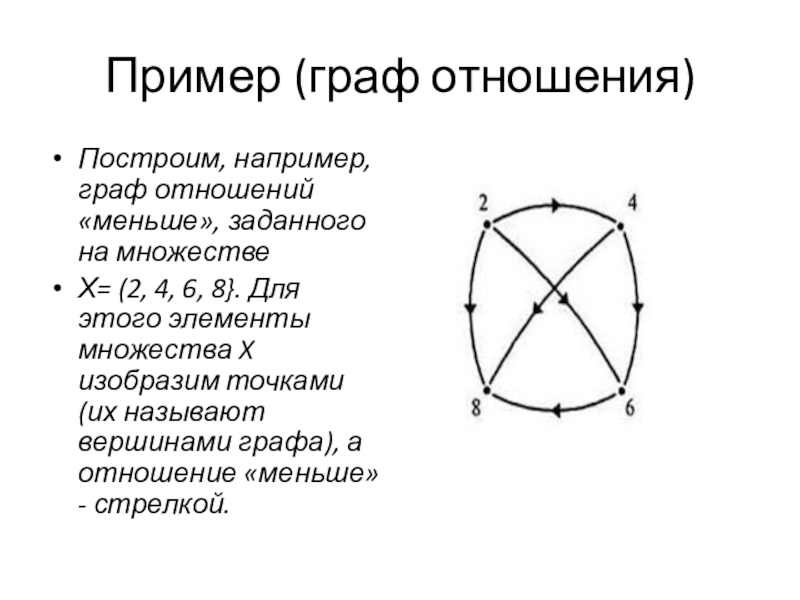
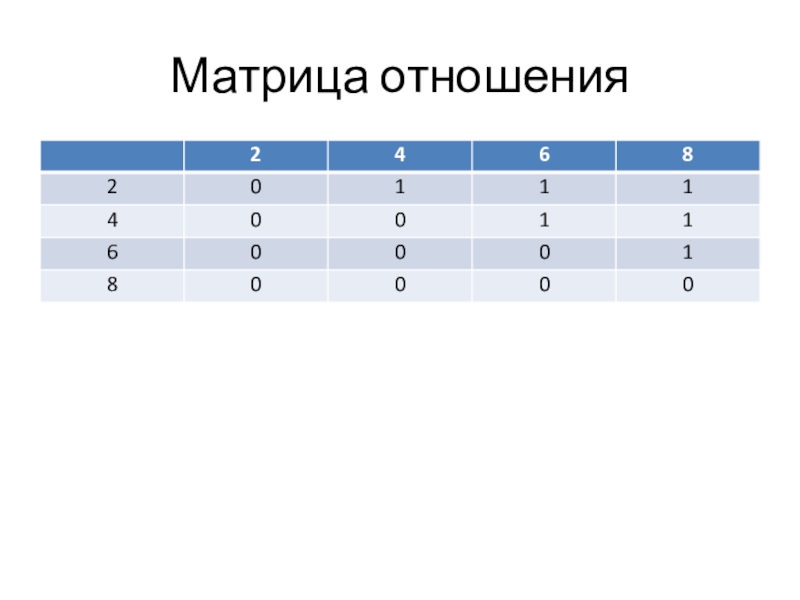
Построим, например, граф отношений «меньше», заданного на множестве
Х= (2, 4, 6, 8}. Для этого элементы множества X
изобразим точками (их называют вершинами графа), а отношение «меньше» - стрелкой.
Слайд 8Свойства бинарных отношений
Свойства бинарных отношений
Бинарное отношение на некотором множестве может
обладать различными свойствами, например:
Рефлексивность:
Антирефлексивность:
Симметричность:
Слайд 9Свойства бинарных отношений
Антисимметричность:
Асимметричность:
Транзитивность:
Слайд 10Рефлексивное отношение
Если отношение R рефлексивно на множестве X, то в
каждой вершине графа данного отношения имеется петля. Справедливо и обратное
утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности.
Матрица – на главной диагонали единицы.
Слайд 11Рефлексивное отношение
Примеры рефлексивных отношений:
- отношение «кратно» на множестве натуральных чисел
(каждое натуральное число кратно самому себе);
- отношение подобия треугольников (каждый
треугольник подобен самому себе).
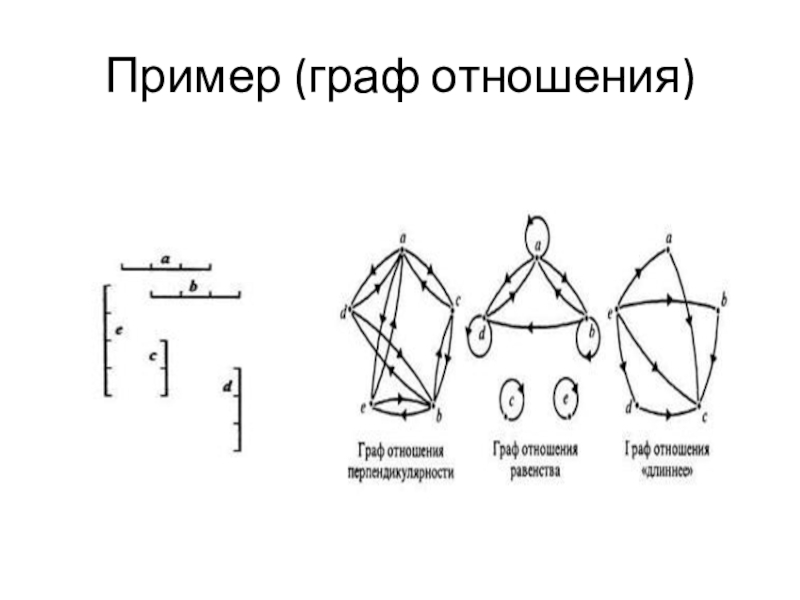
Существуют отношения, которые свойством рефлексивности на обладают. Таким, например, является отношение перпендикулярности на множестве отрезков: нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе. Поэтому на графе отношения перпендикулярности нет ни одной петли. Не обладает свойством рефлексивности и отношение «длиннее» для отрезков.
Слайд 12Симметричные отношения
Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой,
идущей от х к у, граф содержит и стрелку, идущую
от у к х. Справедливо и обратное утверждение. Граф, содержащий вместе с каждой стрелкой, идущей от х к у, и стрелку, идущую от у к х, является графом симметричного отношения.
Матрица – симметрична относительно главной диагонали.
Слайд 13Симметричные отношения
Примеры
- отношение параллельности на множестве прямых (если прямая х
параллельна прямой у, то и прямая у параллельна прямой х);
-
отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).
Существуют отношения, которые свойством симметричности не обладают. Таким, например, является отношение «длиннее» на множестве отрезков. Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х.
Слайд 14Транзитивные отношения
Граф транзитивного отношения с каждой парой стрелок, идущих от х к у и у к z,
содержит стрелку, идущую от х к z. Справедливо и обратное утверждение.
Слайд 15Транзитивные отношения
Кроме отношения «длиннее» на множестве отрезков свойством транзитивности обладает
отношение равенства: если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z.
Это свойство отражено и на графе отношения равенства.
Существуют отношения, которые свойством транзитивности не обладают. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны!
Слайд 16Виды отношений
Рефлексивное и транзитивное отношение называется отношением квазипорядка
Рефлексивное, симметричное и транзитивное
отношение называется отношением эквивалентности.
Рефлексивное, антисимметричное и транзитивное отношение называется отношением нестрого порядка.
Антирефлексивное,
асимметричное и транзитивное отношение называется отношением нестрого порядка.
Слайд 17Отношение эквивалентности
Примерами отношений эквивалентности могут служить отношения равенства геометрических фигур,
отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).
Слайд 18Разбиение на классы
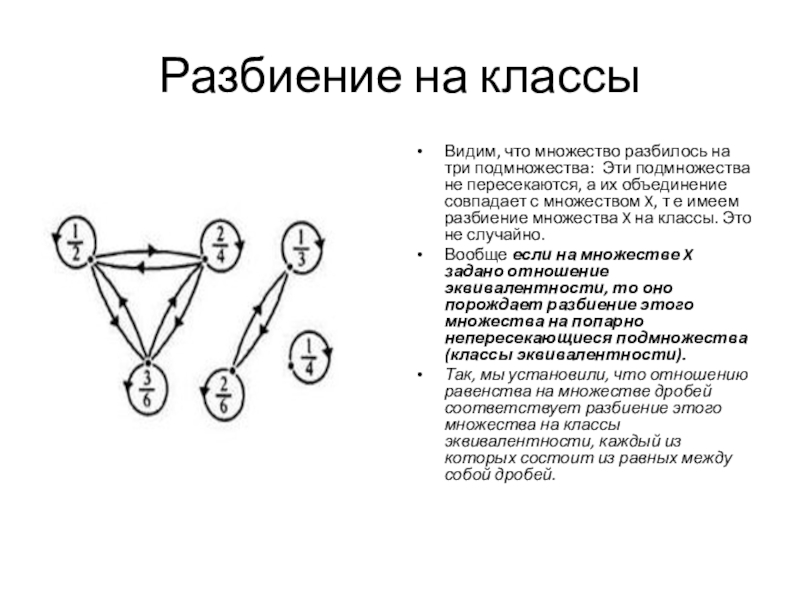
Видим, что множество разбилось на три подмножества: Эти подмножества
не пересекаются, а их объединение совпадает с множеством X, т
е имеем разбиение множества X на классы. Это не случайно.
Вообще если на множестве X задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества (классы эквивалентности).
Так, мы установили, что отношению равенства на множестве дробей соответствует разбиение этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.
Слайд 19Задачи для самостоятельного решения
R1 «иметь один и тот же остаток от
деления на 5»; M1 множество чисел {1,2,…., 15}.
R2 «быть равным»; M2 множество чисел
{1,2,3,4,5,6,7,8,9} .
R3 «жить в одном городе»; M3 множество людей.
R4 «быть знакомым»; M4 множество людей.
R5 {(a,b):(a-b) - чётное; M5 множество чисел {1,2,3,4,5,6,7,8,9}.
R6 {(a,b):(a+b) - чётное; M6 множество чисел {1,2,3,4,5,6,7,8,9}.
R7 {(a,b):(a+1) - делитель (a+b)} ; M7 - множество {1,2,3,4,5,6,7,8,9}.
R8 {(a,b):a - делитель (a+b),a≠1}; M8 - множество чисел
{1,2,…., 15}.
R9 «быть сестрой»; M9 - множество людей.
R10 «быть дочерью»; M10 - множество людей.