Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
П О З Д Р А В Л Я Е М !
Содержание
- 1. П О З Д Р А В Л Я Е М !
- 2. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- 3. АКТУАЛЬНОСТЬРОЛЬ ТЕОРИИ ВЕРОЯТНОСТЕЙ:ПОЗВОЛЯЕТ ЛУЧШЕ ОРИЕНТИРОВАТЬСЯ В ОКРУЖАЮЩЕМ
- 4. Лекция 1. ОСНОВЫТЕОРИИ ВЕРОЯТНОСТЕЙ
- 5. Часть I.СЛУЧАЙНЫЕ СОБЫТИЯ
- 6. 1. ВИДЫ СОБЫТИЙ ВСЕ СОБЫТИЯ В ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 7. Статистические закономерностиСЛУЧАЙНЫЕ СОБЫТИЯ ИМЕЮТ ПРИЧИНЫ, И В
- 8. МНОЖЕСТВОСЛУЧАЙНЫХ СОБЫТИЙ КАК БЫ ОГРАНИЧЕНО С ДВУХ
- 9. ДОСТОВЕРНОЕ – СОБЫТИЕ, КОТОРОЕ В ДАННОМ ИСПЫТАНИИ
- 10. Среди НЕСКОЛЬКИХ случайных событий могут быть событияРАВНОВОЗМОЖНЫЕ,НЕСОВМЕСТНЫЕ, ПРОТИВОПОЛОЖНЫЕ?
- 11. Равновозможные событияСобытия называются равновозможными,если не существует причин,
- 12. Несовместные событияСобытия называются несовместными,если появление одного из
- 13. Противоположные событияДва события называются
- 14. Примечание ЛЮБЫЕ ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ НЕСОВМЕСТНЫ. Обратное утверждение в общем случаеневерно.
- 15. 2. КОМБИНАЦИИ СОБЫТИЙРАССМОТРИМ ДВЕ КОМБИНАЦИИ СОБЫТИЙ:СУММУИПРОИЗВЕДЕНИЕ.ОБОЗНАЧЕНИЕ этих
- 16. Сумма событийСУММА СОБЫТИЙ –это событие, состоящее в
- 17. Произведение событийПРОИЗВЕДЕНИЕ СОБЫТИЙ –это событие, состоящее в
- 18. 3. ПОНЯТИЕ ВЕРОЯТНОСТИВЕРОЯТНОСТЬ ЕСТЬ КОЛИЧЕСТВЕННАЯ МЕРА ВОЗМОЖНОСТИ
- 19. Классическое определение вероятности ВЕРОЯТНОСТЬЮСОБЫТИЯ «А» НАЗЫВАЕТСЯ ОТНОШЕНИЕ ЧИСЛА
- 20. Предварительные пояснения к статистическому определению вероятности Пусть
- 21. Статистическое определение вероятности ВЕРОЯТНОСТЬЮСОБЫТИЯ А НАЗЫВАЕТСЯ ПРЕДЕЛ ОТНОСИТЕЛЬНОЙ
- 22. Следствия из определений вероятности ВЕРОЯТНОСТЬ НЕВОЗМОЖНОГО СОБЫТИЯ
- 23. 4. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙP(A+B) = P(A) +
- 24. 5. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ В ОБЩЕМ ВИДЕ ТЕОРЕМА
- 25. Формулировка теоремы умножения вероятностейP(AB) = P(A)
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3АКТУАЛЬНОСТЬ
РОЛЬ ТЕОРИИ ВЕРОЯТНОСТЕЙ:
ПОЗВОЛЯЕТ ЛУЧШЕ ОРИЕНТИРОВАТЬСЯ В ОКРУЖАЮЩЕМ МИРЕ, ГДЕ НЕ
ВСЕ ЖЕСТКО ДЕТЕРМИНИРОВАНО;
ЯВЛЯЕТСЯ ОСНОВОЙ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
РОЛЬ МАТЕМАТИЧЕС-КОЙ СТАТИСТИКИ:
НУЖНА ДЛЯ СИСТЕ-МАТИЗАЦИИ
И ОЦЕНКИ ЭКСПЕРИ-МЕНТАЛЬНЫХ ДАН-НЫХ В ПРОЦЕССЕ РЕШЕНИЯ НАУЧНЫХ И ПРАКТИЧЕСКИХ ЗАДАЧЛЕЖИТ В ОСНОВЕ МЕДИЦИНСКОЙ СТАТИСТИКИ
Слайд 61. ВИДЫ СОБЫТИЙ
ВСЕ СОБЫТИЯ
В ТЕОРИИ ВЕРОЯТНОСТЕЙ
ПРИНЯТО ОБОЗНАЧАТЬ
ЗАГЛАВНЫМИ
БУКВАМИ
ЛАТИНСКОГО АЛФАВИТА: A, B, C, …
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ ОПЕРИРУЕТ
СЛУЧАЙНЫМИ
СОБЫТИЯМИ.
СЛУЧАЙНОЕ –
СОБЫТИЕ, КОТОРОЕ
В ДАННОМ ИСПЫТАНИИ МОЖЕТ ПРОИЗОЙТИ,
А МОЖЕТ И НЕ
ПРОИЗОЙТИ.
Примеры:
падение монеты определенной стороной вверх;
выпадение определенного числа очков на кубике для настольной игры.
Слайд 7Статистические закономерности
СЛУЧАЙНЫЕ СОБЫТИЯ ИМЕЮТ ПРИЧИНЫ,
И В МИРЕ ЭТИХ СОБЫТИЙ
СУЩЕСТВУЮТ ЗАКОНОМЕРНОСТИ.
ОДНАКО ПРОЯВЛЯЮТСЯ ОНИ ЛИШЬ ПРИ БОЛЬШОМ ЧИСЛЕ ИСПЫТАНИЙ.
ТАКИЕ ЗАКОНОМЕРНОСТИ НАЗЫВАЮТСЯ
СТАТИСТИЧЕСКИМИ.
Пример - основной закон радиоактивного распада.
Слайд 8
МНОЖЕСТВО
СЛУЧАЙНЫХ СОБЫТИЙ КАК БЫ ОГРАНИЧЕНО С ДВУХ СТОРОН
СОБЫТИЯМИ
НЕВОЗМОЖНЫМИ
И
ДОСТОВЕРНЫМИ.
НЕВОЗМОЖНОЕ – СОБЫТИЕ, КОТОРОЕ В ДАННОМ ИСПЫТАНИИ
НЕ МОЖЕТ ПРОИЗОЙТИ.
Например,
если на гранях кубика число
очков от 1 до 6, то
выпадение семи очков при единичном
бросании кубика –
невозможное событие.
Слайд 9
ДОСТОВЕРНОЕ –
СОБЫТИЕ, КОТОРОЕ В ДАННОМ ИСПЫТАНИИ ОБЯЗАТЕЛЬНО ПРОИЗОЙДЕТ
(НЕ
МОЖЕТ НЕ ПРОИЗОЙТИ).
Например, если
в некоторой корзине
(часто говорят
"в урне") имеются ТОЛЬКО КРАСНЫЕ ШАРЫ,
ТО ВЫТАСКИВАНИЕ ИЗ НЕЕ ИМЕННО КРАСНОГО ШАРА – событие ДОСТОВЕРНОЕ.
В то же время вытаскивание черного шара – событие невозможное.
Слайд 10Среди НЕСКОЛЬКИХ случайных событий могут быть события
РАВНОВОЗМОЖНЫЕ,
НЕСОВМЕСТНЫЕ,
ПРОТИВОПОЛОЖНЫЕ
?
Слайд 11Равновозможные события
События называются равновозможными,
если не существует причин,
в силу которых
одно из них происходило бы чаще других.
Пример
В урне 2 КРАСНЫХ
и 2 ЧЕРНЫХ шара.
Тогда
ВЫТАСКИВАНИЕ КРАСНОГО ШАРА
и ВЫТАСКИВАНИЕ ЧЕРНОГО ШАРА – события РАВНОВОЗМОЖНЫЕ.
Слайд 12Несовместные события
События называются несовместными,
если появление одного из них в данном
испытании
исключает появление других в том же испытании.
Пример
Имеется урна
с красными и черными шарами.Предполагается, что в руке помещается только один шар.
Тогда ПОЯВЛЕНИЕ при ЕДИНИЧНОМ вытаскивании
одновременно
КРАСНОГО ШАРА и ЧЕРНОГО ШАРА –
события НЕСОВМЕСТНЫЕ.
Слайд 13Противоположные события
Два события
называются
противоположными,
если одно из
них заключается в том, что другое
не происходит.
Т.е., вместе
они охватывают все возможные итоги испытания. ОБОЗНАЧЕНИЕ:
(читается "А" и "НЕ А").
Пример
Выпадение орла и
выпадение решки
при единичном бросании монеты –
противоположные события
(если исключить возмож-
ность установки монеты
на ребро).
и
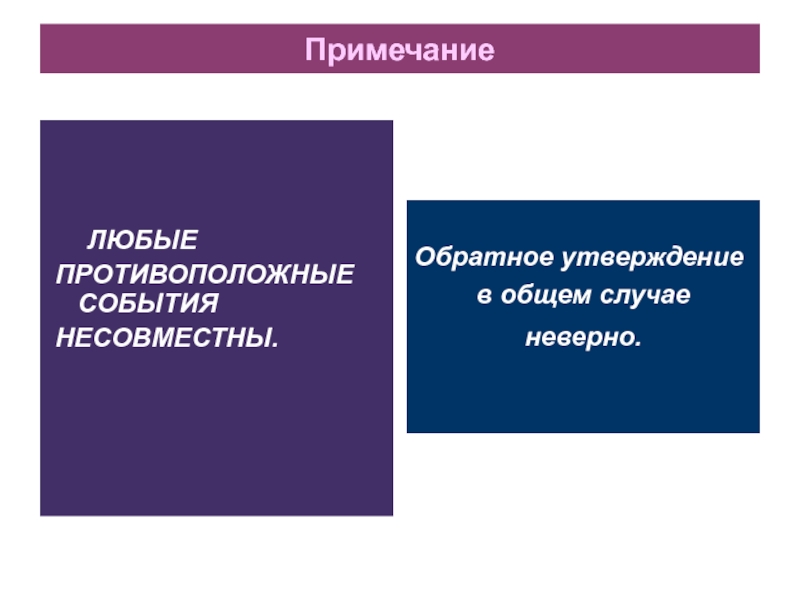
Слайд 14Примечание
ЛЮБЫЕ
ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ
НЕСОВМЕСТНЫ.
Обратное утверждение
в общем случае
неверно.
Слайд 152. КОМБИНАЦИИ СОБЫТИЙ
РАССМОТРИМ ДВЕ КОМБИНАЦИИ СОБЫТИЙ:
СУММУ
И
ПРОИЗВЕДЕНИЕ.
ОБОЗНАЧЕНИЕ этих комбинаций
ДЛЯ ДВУХ СОБЫТИЙ,
СОБЫТИЯ А И СОБЫТИЯ В :
сумма – «А + В»,
произведение
– «А · В».Слайд 16Сумма событий
СУММА СОБЫТИЙ –
это событие, состоящее в том,
что происходит
ИЛИ
А, ИЛИ В, ИЛИ ОНИ ОБА ВМЕСТЕ.
ИНАЧЕ:
ЕСЛИ ПРОИСХОДИТ ХОТЯ
БЫ ОДНО ИЗ НИХ. СОЮЗЫ "ИЛИ", "ХОТЯ БЫ" – УКАЗАНИЕ НА СУММУ СОБЫТИЙ.
Слайд 17Произведение событий
ПРОИЗВЕДЕНИЕ СОБЫТИЙ –
это событие, состоящее в том,
что происходит
И
А, И В,
Т.Е. ОНИ ПОЯВЛЯЮТСЯ ОБА, СОВМЕСТНО.
СОЮЗ "И" –
УКАЗАНИЕ НА ПРОИЗВЕДЕНИЕ СОБЫТИЙ.ПРОИЗВЕДЕНИЕ НЕСОВМЕСТНЫХ СОБЫТИЙ ЕСТЬ СОБЫТИЕ НЕВОЗМОЖНОЕ.
Слайд 183. ПОНЯТИЕ ВЕРОЯТНОСТИ
ВЕРОЯТНОСТЬ ЕСТЬ КОЛИЧЕСТВЕННАЯ МЕРА ВОЗМОЖНОСТИ СОБЫТИЯ.
Существует несколько
определений
вероятности.
Чаще всего используются КЛАССИЧЕСКОЕ и СТАТИСТИЧЕСКОЕ определения.
Слайд 19Классическое определение вероятности
ВЕРОЯТНОСТЬЮ
СОБЫТИЯ «А» НАЗЫВАЕТСЯ
ОТНОШЕНИЕ ЧИСЛА m
БЛАГОПРИЯТСТВУ-ЮЩИХ «А»
ИСХОДОВ ИСПЫТАНИЯ К ОБЩЕМУ ЧИСЛУ n
ВСЕХ ВОЗМОЖНЫХ
ИСХОДОВ ИСПЫТАНИЯ.
Так, если
в урне 2 красных и 3 белых шара, то вероятность вытащить при единич-ном испытании красный шар - 2/5, белый шар – 3/5.
Слайд 20Предварительные пояснения к статистическому определению вероятности
Пусть производится серия из
n испытаний,
и в этой серии событие А происходит m раз.
Число
m называется ЧАСТОТОЙ, а отношение m к n W(A) = m / n –
ОТНОСИТЕЛЬНОЙ ЧАСТОТОЙ
события А.
Если число испытаний в
серии достаточно велико,
то относительная частота
события - его устойчивая характеристика:
она почти не меняется
от серии к серии.
Слайд 21Статистическое определение вероятности
ВЕРОЯТНОСТЬЮ
СОБЫТИЯ А НАЗЫВАЕТСЯ
ПРЕДЕЛ ОТНОСИТЕЛЬНОЙ ЧАСТОТЫ
ЭТОГО СОБЫТИЯ
ПРИ
НЕОГРАНИЧЕННОМ
УВЕЛИЧЕНИИ ЧИСЛА ИСПЫТАНИЙ:
Если n достаточно
велико, то
Это –
«опытная вероят-ность». Именно она обычно определяется на практике.Слайд 22Следствия из определений вероятности
ВЕРОЯТНОСТЬ НЕВОЗМОЖНОГО СОБЫТИЯ РАВНА НУЛЮ.
ВЕРОЯТНОСТЬ ДОСТОВЕРНОГО
СОБЫТИЯ РАВНА ЕДИНИЦЕ.
ВЕРОЯТНОСТЬ ЛЮБОГО СЛУЧАЙ-НОГО СОБЫТИЯ МОЖЕТ ПРИНИМАТЬ ЗНАЧЕНИЯ ЛИШЬ
В ИНТЕРВАЛЕ МЕЖДУ ЭТИМИ ЧИСЛАМИ:0 ≤ P(A) ≤ 1.
Слайд 234. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
P(A+B) = P(A) + P(B) – P(AB).
ЧАСТНЫЙ
СЛУЧАЙ
ДЛЯ НЕСОВМЕСТНЫХ СОБЫТИЙ:
P(A+B) = P(A) + P(B).
Слайд 245. ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
В ОБЩЕМ ВИДЕ
ТЕОРЕМА УМНОЖЕНИЯ СПРАВЕДЛИВА ДЛЯ
ЛЮБЫХ,
В ТОМ ЧИСЛЕ
ЗАВИСИМЫХ, СОБЫТИЙ.
СОБЫТИЕ B
ЗАВИСИТ
ОТ СОБЫТИЯ А,
ЕСЛИ
ВЕРОЯТНОСТЬ B
ЗАВИСИТ ОТ ТОГО,
ПРОИЗОШЛО ЛИ А.
Слайд 25Формулировка теоремы умножения
вероятностей
P(AB) = P(A) ∙ P(B/A).
Здесь P(B/A) –
условная вероятность события В,
т.е. вероятность В при условии, что
А произошло.Для НЕЗАВИСИМЫХ событий
P(AB) = P(A) ∙ P(B).