Слайд 1ВВЕДЕНИЕ В ГЕОМЕХАНИКУ МЕСТОРОЖДЕНИЙ УГЛЕВОДОРОДОВ
Семестровый курс
Лекция 6
Слайд 2Применение алгоритмов нелинейной динамики при анализе геомеханических процессов.
Временные ряды
сейсмических наблюдений. Представление сейсмического режима в фазовом пространстве. Фазовая точка
и фазовая траектория.
Динамические системы и их устойчивость. Аттракторы, их типы и физический смысл. Фрактальная размерность аттракторов. Бифуркации. Инерциальные многообразия. Параметры порядка.
Слайд 3Реконструкция аттракторов по временным рядам. Теорема Такенса. Метод Грасбергера –
Прокачи оценки размерности аттракторов.
Прогнозные возможности методов нелинейной динамики при
анализе временных рядов и пространственно распределенных событий.
Практическое применение методов обработки данных пассивного сейсмического мониторинга для поиска и оптимизации разработки месторождений углеводородов. Выявление активных тектонических разломов. Взаимосвязь между сейсмической активностью и параметрами эксплуатации месторождения нефти. Опыт анализа микросейсмов при поиске месторождений газа.
Слайд 5Временные ряды
При обработке экспериментальных временных рядов обычно решают несколько типов
задач.
Задачи измерения некоторых характеристик динамических систем, инвариантных относительно замены
переменных. К ним относятся размерности аттрактора, ляпуновские показатели, энтропии. Может быть поставлена задача аппроксимации уравнений движения по экспериментальным данным, выбор модели для наилучшего описания данных.
Задачи динамического прогноза временных рядов. В этом случае, тоже приходится решать задачу восстановления динамической системы по временному ряду, но собственно уравнения движения интереса не предоставляют, к ним относятся как к черному ящику – важно, чтобы по входному сигналу правильно вырабатывался выходной.
Задачи идентификации, когда нужно каким-либо образом классифицировать исследуемые системы для диагностических целей. При этом абсолютно несущественно, измеряются ли инвариантные характеристики динамической системы или что-нибудь другое, пригодное только для узкого круга задач.
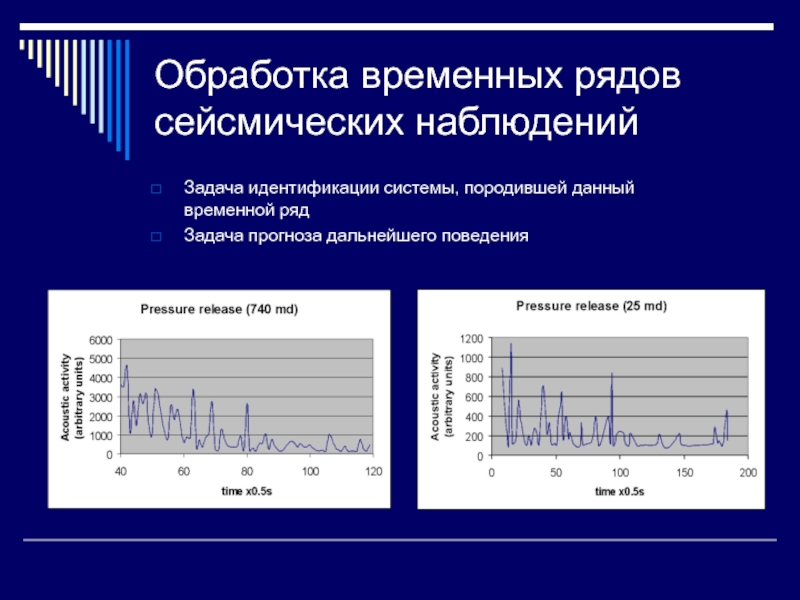
Слайд 6Обработка временных рядов сейсмических наблюдений
Задача идентификации системы, породившей данный временной
ряд
Задача прогноза дальнейшего поведения
Слайд 7Динамические системы
Система обыкновенных дифференциальных уравнений
Автономная система обыкновенных дифференциальных уравнений
Математическая модель
некоторой механической системы
Слайд 8Динамические системы
Фазовое пространство P
Однопараметрическая непрерывная или дискретная группа (полугруппа) его
преобразований
Слайд 9Динамические системы
Система называется динамической, если задание начальных условий полностью определяет
ее поведение в последующие моменты времени.
Пример нединамической системы – бросание
монеты орел-решка. Каждое следующее испытание не зависит от предыдущего.
В большинстве случаев динамическая система задается системой дифференциальных уравнений.
Слайд 10Фазовое пространство
Рассмотрим физическую систему, описываемую уравнениями первого порядка:
Состояние системы в
каждый данный момент времени полностью определяется заданием n чисел yi.
Введем n-мерное пространство, по осям координат которого будем откладывать значения yi и производные. Тогда состояние изучаемой системы в каждый данный момент времени представляется некоторой точкой в этом пространстве. Введенное таким образом пространство называется фазовым.
С течением времени состояние системы меняется. Соответственно этому меняется и положение изображающей точки в фазовом пространстве, т.е. эта точкам описывает некоторую кривую, называемую фазовой траекторией.
Совокупность фазовых траекторий, отвечающих различным начальным условиям, образует фазовый портрет системы.
Слайд 12Понятие устойчивости
Устойчивость системы – это ее свойство слабо менять состояние
и/или поведение под действием возмущений.
Устойчивость по Ляпунову – изначально близкие
изображающие точки, принадлежащие разным фазовым траекториям, оказываются близкими и в последующие моменты времени.
Асимптотическая устойчивость. Этот случай характерен для диссипативных систем. Диссипативная система – система с диссипацией. Под диссипацией понимается обмен системы со своим окружением энергией и/или веществом. Система называется асимптотически устойчивой, если две фазовые точки, принадлежащие двум различным фазовым траекториям и достаточно близкие друг к другу в начальный момент времени, неограниченно сближаются по мере движения.
Орбитальная устойчивость (устойчивость по Пуанкаре). Пусть L – некоторая траектория системы, максимально продленная в обе стороны времени. Если изображающая точка системы в некоторым момент времени оказывается достаточно близкой к траектории L, то и при дальнейшем движении эта точка не отойдет далеко от рассматриваемой траектории.
Структурная устойчивость – при различных видах малых воздействий фазовый портрет остается качественно неизменным.

Слайд 13Понятие аттрактора.
Аттрактором называется некоторое компактное асимптотически устойчивое множество в
фазовом пространстве рассматриваемой динамической системы. (Множество М в метрическом пространстве
Х называется компактом в Х, если из любой последовательности точек xn ∈ М можно выделить подпоследовательность, сходящуюся к точке, принадлежащей множеству М.)
Аттрактор – это такое множество, к которому из некоторой его окрестности притягиваются все фазовые траектории.
Пусть в фазовом пространстве выделено некоторое множество L. Это множество называется аттрактором, если оно
Асимптотически устойчиво, т.е. соответствует определению орбитальной устойчивости.
Компактно, что проявляется, в частности, в том, что аттрактор находится в конечной области фазового пространства и представляет собой замкнутое множество.
Неразложимо на отдельные компоненты, т.е. является связным.
Если аттрактор представляет собой замкнутую линию в фазовом пространстве, то каждая точка такой траектории проходится бесконечное число раз (движение периодично)
Слайд 14Типы аттракторов на фазовой плоскости
Слайд 15Понятие бифуркации
Точкой бифуркации называется такое значение параметра, при котором динамическая
система является структурно неустойчивой
Слайд 16Размерность аттрактора
Размерность характеризует сложность аттрактора динамической системы, т.е. позволяет дать
ответ на вопрос, какое минимальное количество переменных должна включать соответствующая
математическая модель, или дать оценку этой величины.
Обычно на асимптотической стадии траектория притягивается к притягивающему множеству, обладающему фрактальной структурой, или фракталу. Аттракторы, имеющие фрактальную структуру, называют странными.
Слайд 17Фрактальная размерность
Пример: результат измерения длины береговой линии по карте зависит
от масштаба карты
Слайд 20Минимальное инерциальное многообразие.
Нестрогое определение: пространство минимальной размерности, содержащее аттрактор, называется
минимальным инерциальным многообразием.
Если система обладает минимальным инерциальным многообразием размерности dN,
то на ассимптотической стадии ее поведение описывается при помощи dN существенных переменных. Число dN называют числом параметров порядка, или числом независимых степеней свободы.
Слайд 21Реконструкция аттракторов по временным рядам.
Скалярный временной ряд: массив из N
чисел, представляющих собой значения некоторой динамической переменной x(t) c постоянным
шагом Δt по времени, т.е. в моменты ti=t0+(i-1) Δt: xi=x(ti), i=1, … , N.
Можно получить удовлетворительную геометрическую картину аттрактора небольшой размерности, если вместо переменных x, входящих в уравнения динамической системы, использовать m-мерные вектора, получаемые из элементов временного ряда Zi={xi, xi+1,…,xi+m-1}
Слайд 22Теорема Такенса
k – мерное многообразие Mk– гладкая k-мерная поверхность
в n-мерном пространстве, которую локально в окрестности каждой точки можно
параметризовать k евклидовыми координатами без n-мерного пространства.
Когда такое многообразие реализуется в виде поверхности Sk в n-мерном пространстве, которая не пересекается сама с собой, то говорят, что оно вложено в Rn.
Вложение - дифференцируемая векторная функция F, определенная на Mk, для которого отображение Mk →Sk является взаимно однозначным и существует обратная дифференцируемая функция F-1, отображающая Sk обратно в Mk.
Sk=F(Mk) и Mk=F-1(Sk)
Выбирая разные F и n, можно получить различные представления одного и того же многообразия. Теперь пусть на многообразии определена векторная функция, нужное количество раз дифференцируемая и отображающая Mk в m-мерное евклидово пространство Rm Будет ли образ Mk являться вложением или нет?
Слайд 23Теорема Такенса
Пусть задана динамическая система ϕt(x) с фазовым пространством P
и рассматривается одномерный временной ряд, образованный значениями некоторой «наблюдаемой» –
скалярной функции состояния динамической системы x(t):
x=h(x(ti))=h(ϕti(x0))
Пусть фазовая траектория системы находится практически на аттракторе, тогда в качестве многообразия Md рассмотрим минимальное инерциальное многообразие (МИМ).
Построим z-вектора. Пусть τ - шаг между элементами временного ряда. Тогда
xi+1= ϕτ(xi) , xi+2= ϕ2τ(xi) , …, xi+m-1= ϕ(m-1)τ(xi)
Слайд 24Теорема Такенса
Введена векторная функция Λ, отображающая вектора xi∈ Md в
точки m-мерного евклидова пространства Rm.
Md, h и ϕt по крайней
мере дважды дифференцируемы, а для всех неподвижных точек и циклов с периодами kτ, kТеорема Такенса утверждает, что типичным свойством отображения Λ будет, то, что при m≥2d+1 оно будет давать вложение Md в Rm.
Слайд 25Корреляционный интеграл
Рассмотрим множество {zi} точек. Мера взаимосвязи точек, удаленных
друг от друга по времени, задается корреляционным интегралом C(ε), который
можно определить как предел:
θ(x)=0 если x<0 и θ(x)=1, если x≥0
Мера - способ определения расстояния между точками множества.
Евклидова мера
Евклидова мера скорректированная на количество точек :
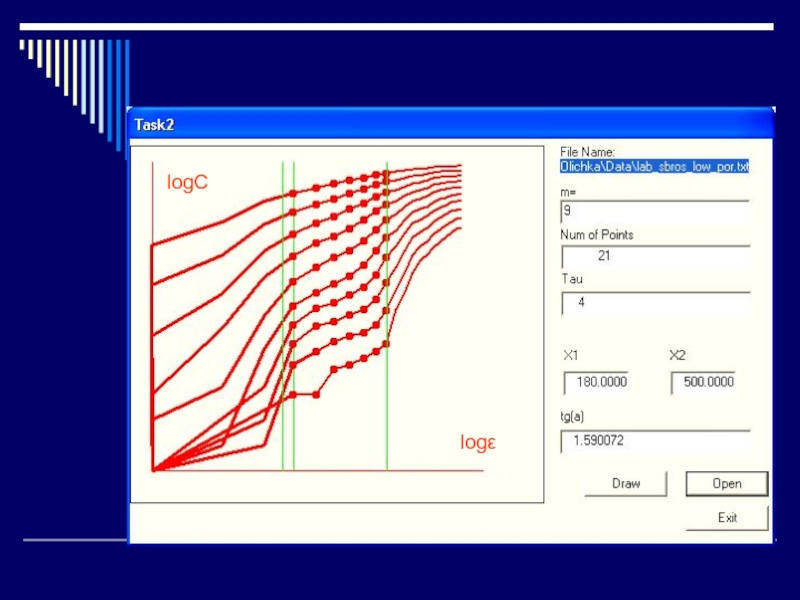
Слайд 26Метод Грасбергера-Прокаччиа
Фрактальная размерность аттрактора
Корреляционная размерность
Фрактальная размерность D аттрактора, характеризующего систему,
представленную временным рядом, оценивается по линейной части этой зависимости
Слайд 28Метод Грасбергера-Прокаччиа
Задают величины m, ε, τ (из разных соображений).
Изменяя ε,
рассчитывают C(ε)
Увеличивая m, получают семейство зависимостей C(ε)
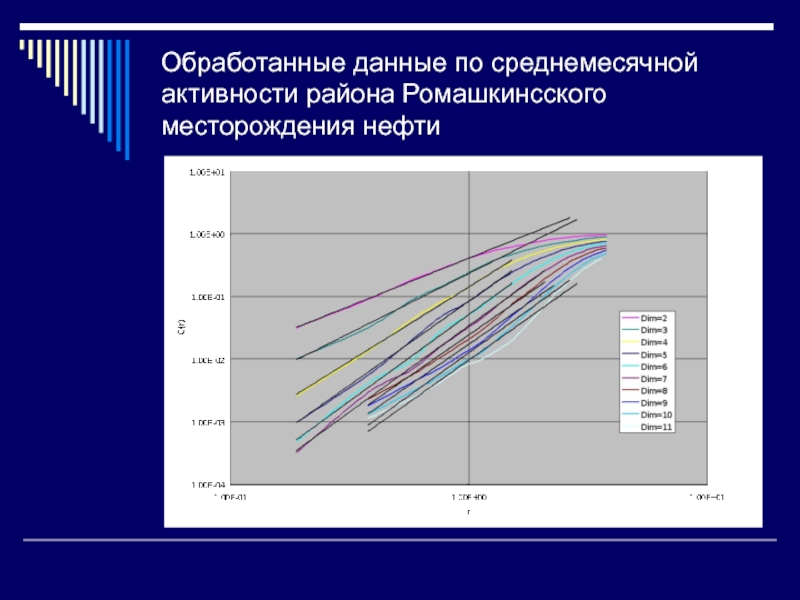
Для линейных участков lgC(lgε)
определяют углы наклона, т.о. определяют D.
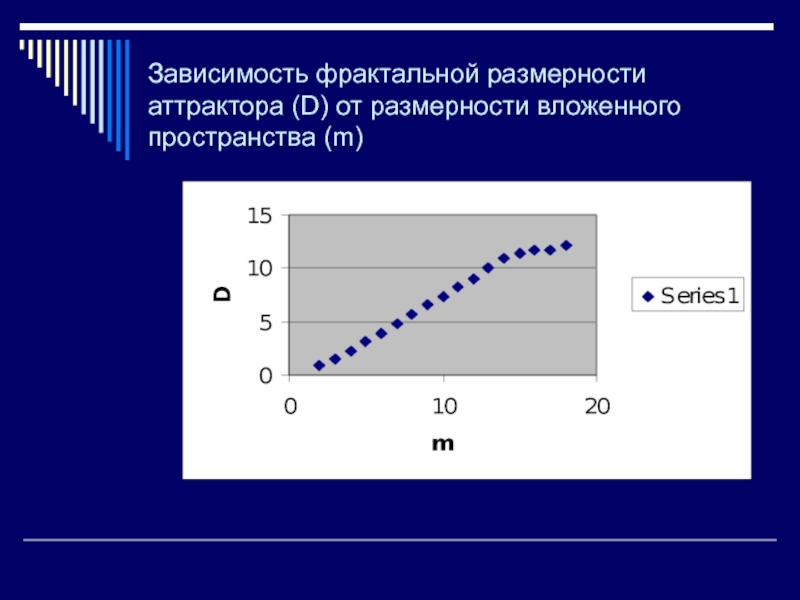
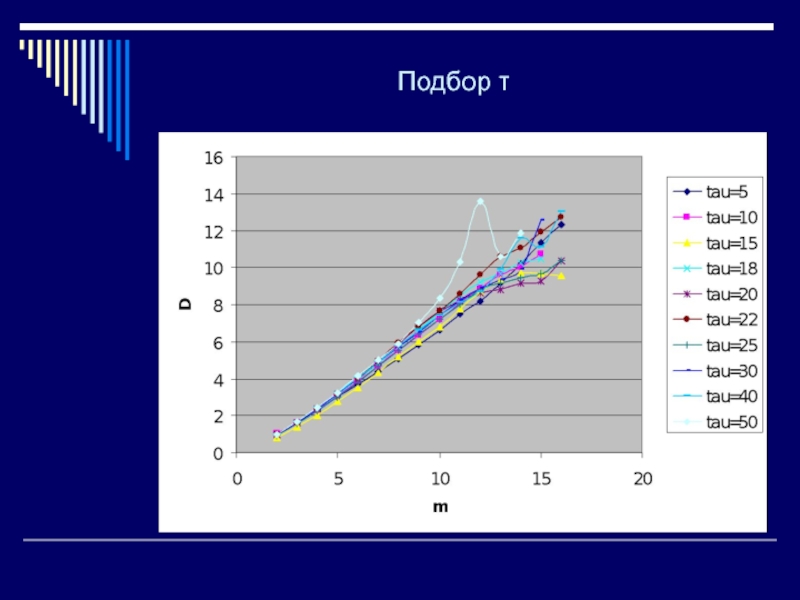
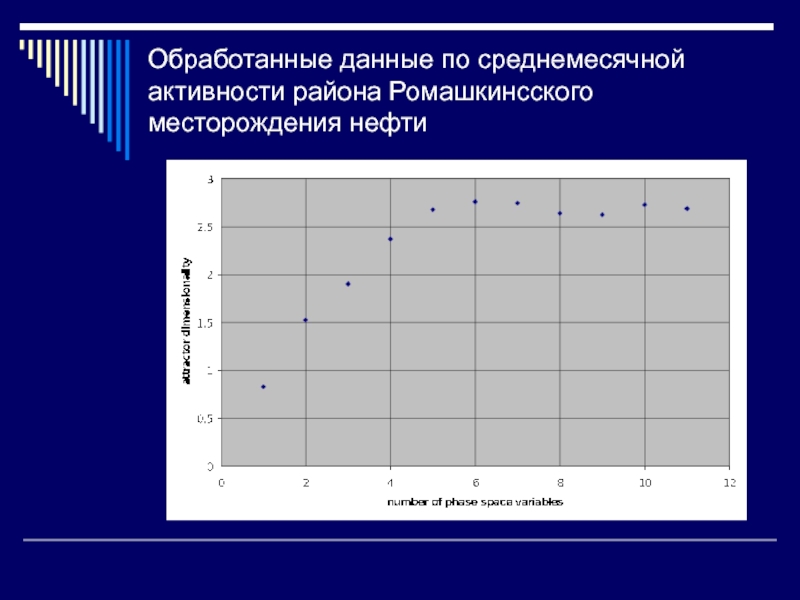
Строят зависимость D(m)
Определяют точку D*, m* выхода зависимости D(m) на «плато».
Варьируя τ оценивают устойчивость зависимостей D(m) при изменении τ, выбирают оптимальное значение τ
Значения D*, m* принимают в качестве оценки фрактальной размерности аттрактора и размерности вложенного пространства (количества определяющих параметров)
Слайд 29Зависимость фрактальной размерности аттрактора (D) от размерности вложенного пространства (m)
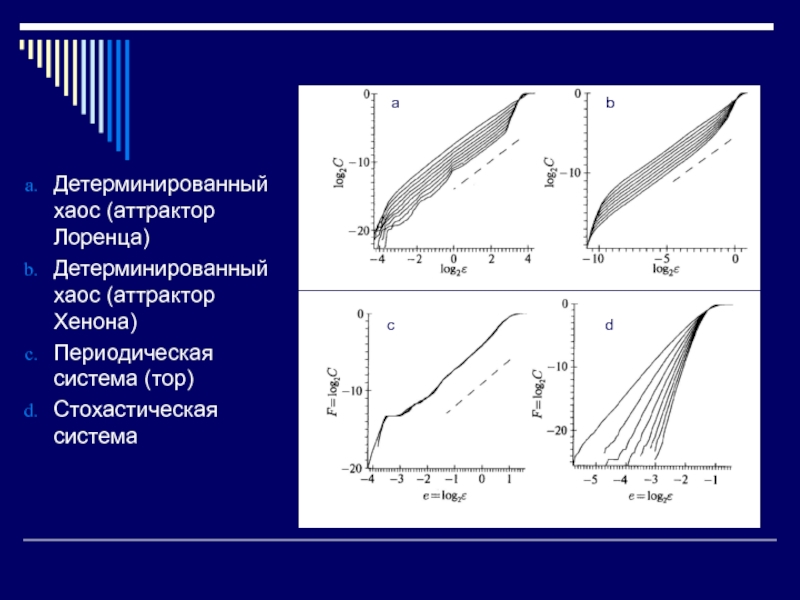
Слайд 31Детерминированный хаос (аттрактор Лоренца)
Детерминированный хаос (аттрактор Хенона)
Периодическая система (тор)
Стохастическая система
a
b
d
c
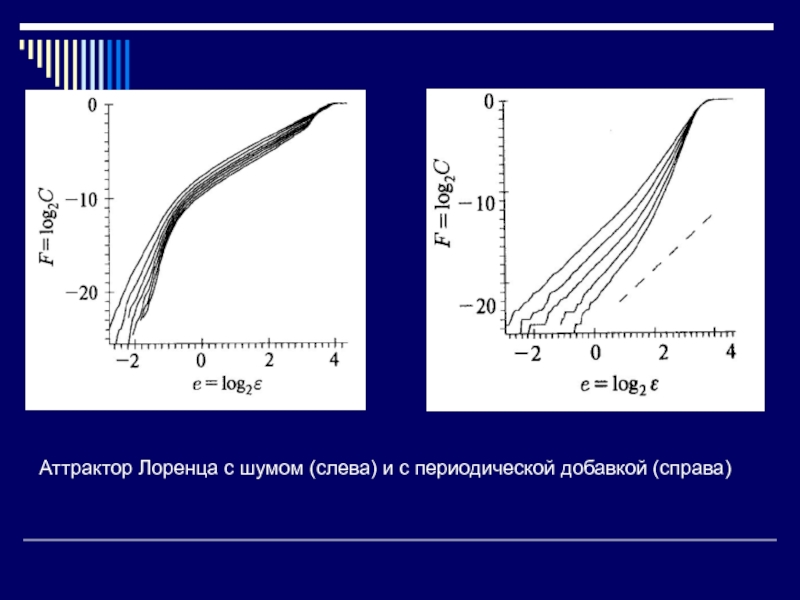
Слайд 32Аттрактор Лоренца с шумом (слева) и с периодической добавкой (справа)
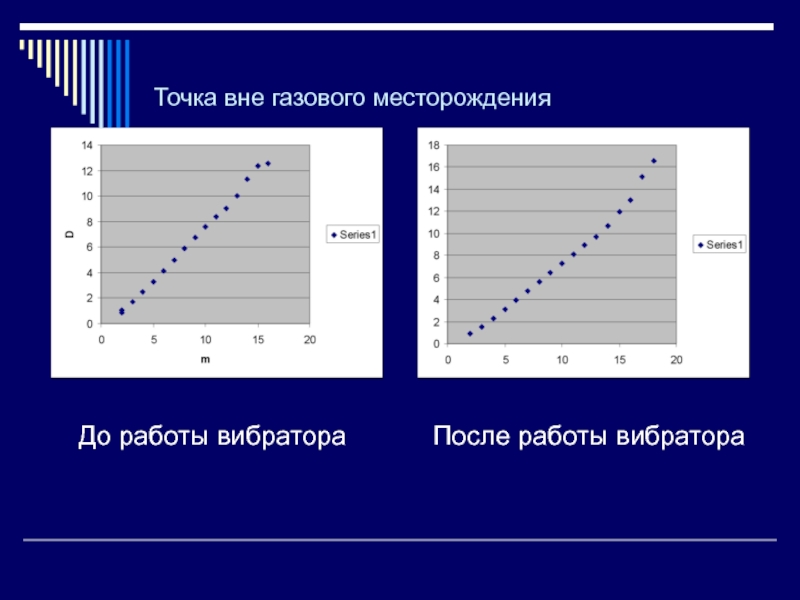
Слайд 33Точка вне газового месторождения
До работы вибратора
После работы вибратора
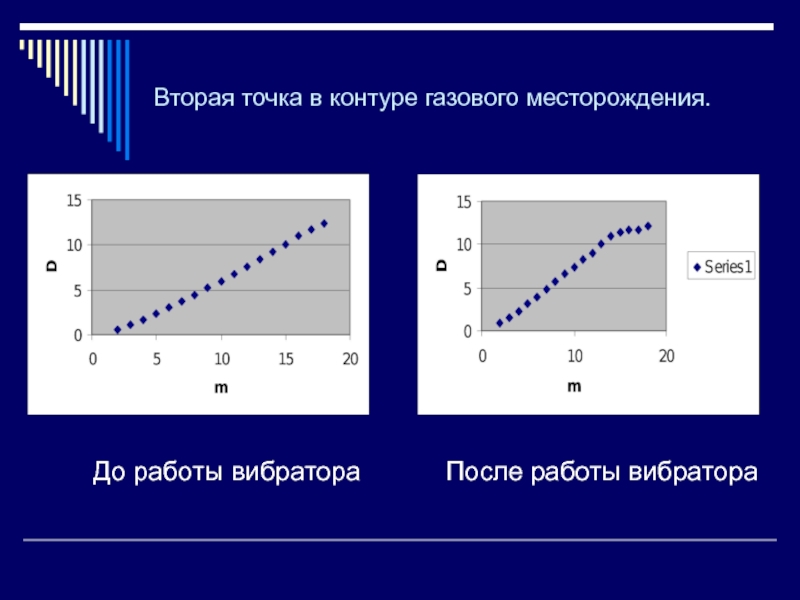
Слайд 34Вторая точка в контуре газового месторождения.
До работы вибратора
После работы вибратора
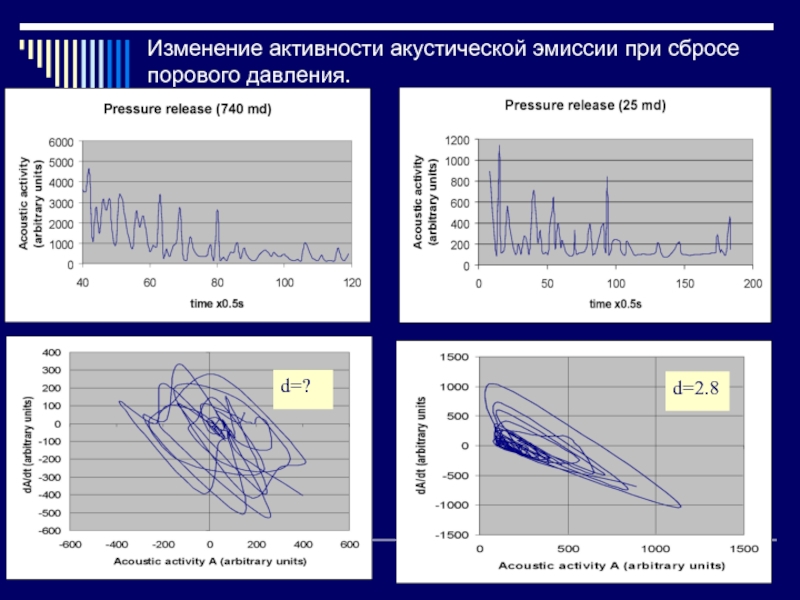
Слайд 35Изменение активности акустической эмиссии при сбросе порового давления.
d=2.8
d=?
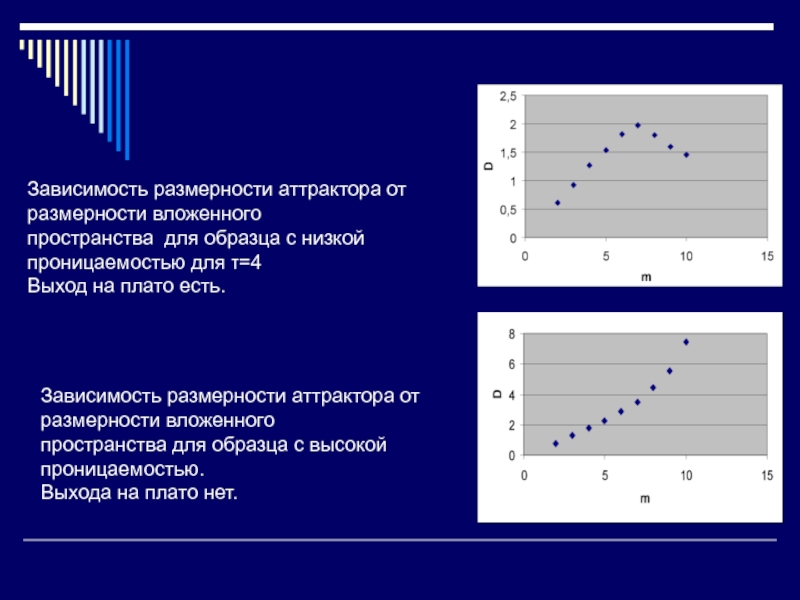
Слайд 36Зависимость размерности аттрактора от размерности вложенного
пространства для образца с высокой
проницаемостью.
Выхода на плато нет.
Зависимость размерности аттрактора от размерности вложенного
пространства для
образца с низкой проницаемостью для τ=4
Выход на плато есть.
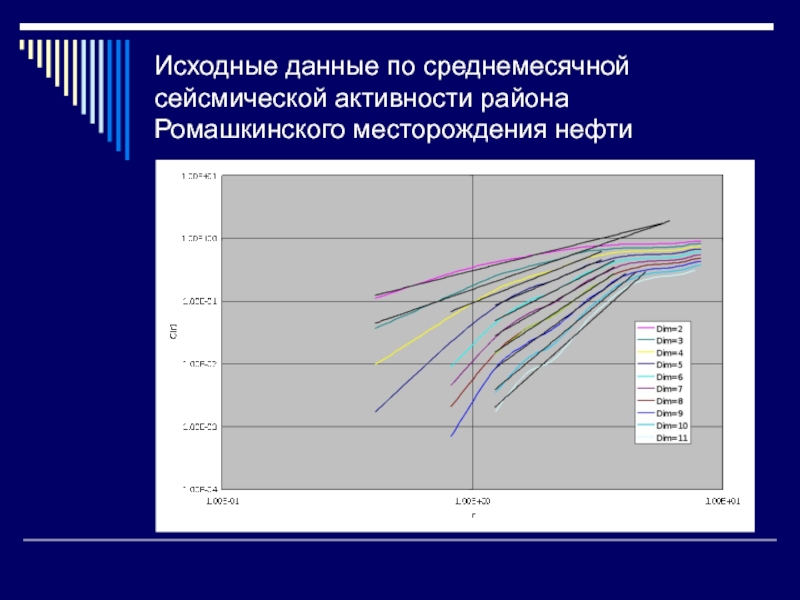
Слайд 37Исходные данные по среднемесячной сейсмической активности района Ромашкинского месторождения нефти
Слайд 38Обработанные данные по среднемесячной активности района Ромашкинсского месторождения нефти
Слайд 39Обработанные данные по среднемесячной активности района Ромашкинсского месторождения нефти
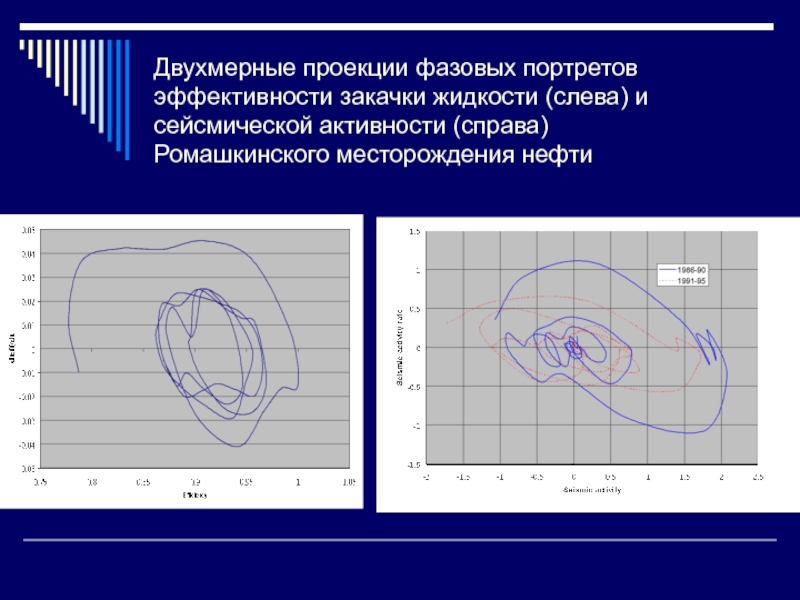
Слайд 40Двухмерные проекции фазовых портретов эффективности закачки жидкости (слева) и сейсмической
активности (справа) Ромашкинского месторождения нефти
Слайд 41Литература
Пригожин И. От существующего к возникающему.
Малинецкий Г.Г., Потапов А.Б. Современные
проблемы нелинейной динамики.
Хакен Г. Синергетика.