по модулю силы, не лежащие на одной прямой
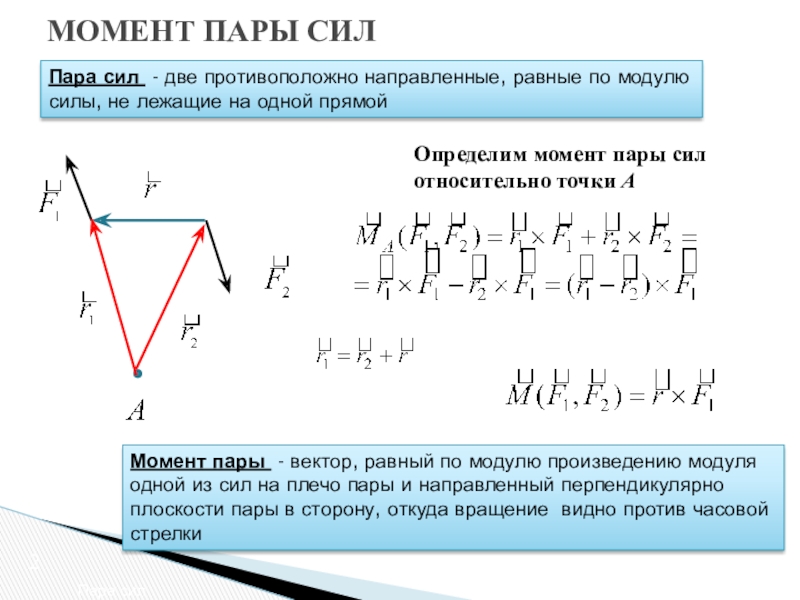
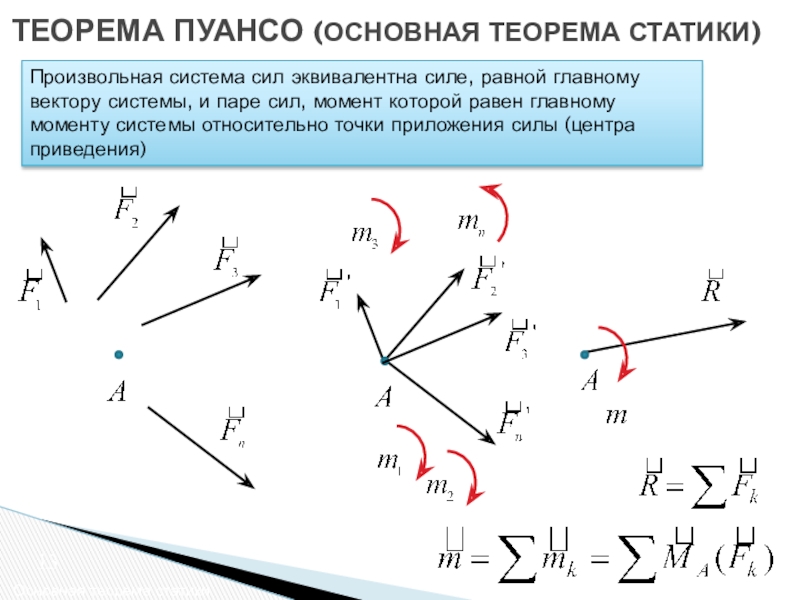
Определим момент пары
сил относительно точки А
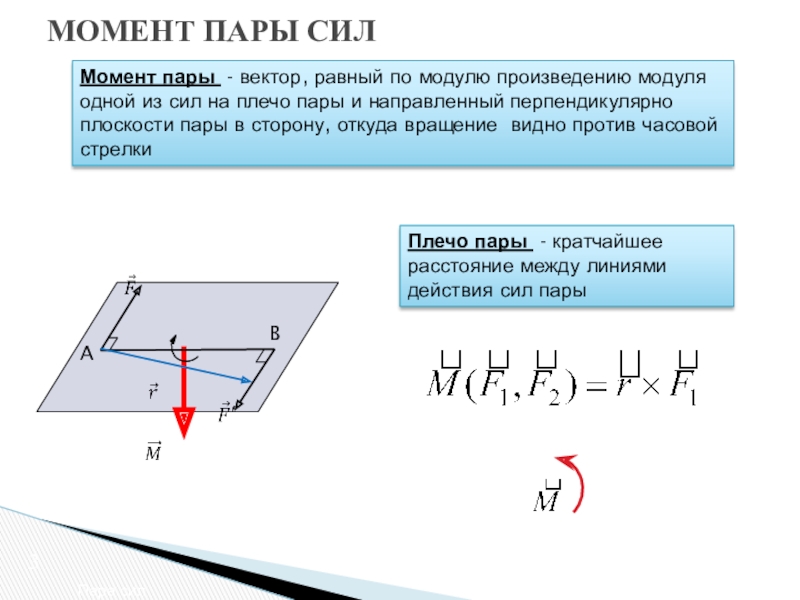
Момент пары - вектор, равный по модулю произведению модуля одной из сил на плечо пары и направленный перпендикулярно плоскости пары в сторону, откуда вращение видно против часовой стрелки