Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
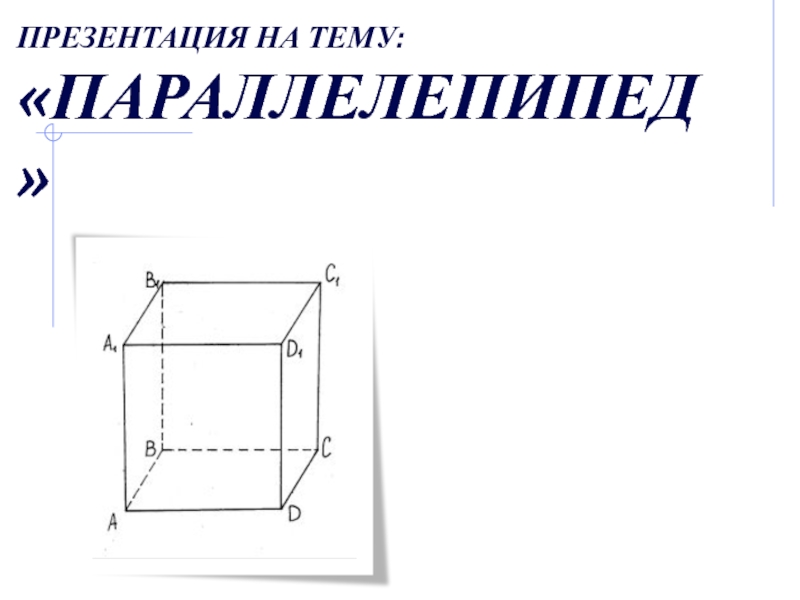
параллелепипед
Содержание
- 1. параллелепипед
- 2. Параллелепипед-четырехугольная призма, основаниями которой являются параллелограммы. Все шесть граней параллелепипеда- параллелограммы.
- 3. Ребра (12)Боковые грани (4)Вершины (8)Основания (2)
- 4. АВСА1DD1B1C1Противоположные грани параллелепипеда параллельны и равны
- 5. Свойства параллелепипеда (1)Диагонали параллелепипеда пересекаются в одной
- 6. Свойства
- 7. Свойства
- 8. Свойства
- 9. Прямой параллелепипедЕсли боковые ребра параллелепипеда перпендикулярны плоскости
- 10. наклонный параллелепипедНаклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, относительно оснований, под не прямым углом.
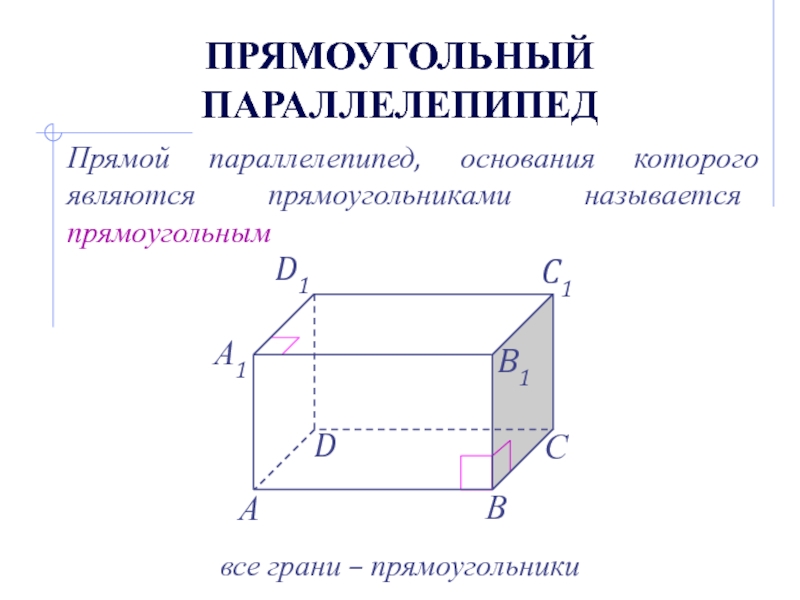
- 11. Прямоугольный параллелепипедПрямой параллелепипед, основания которого являются прямоугольниками называется прямоугольнымвсе грани – прямоугольники
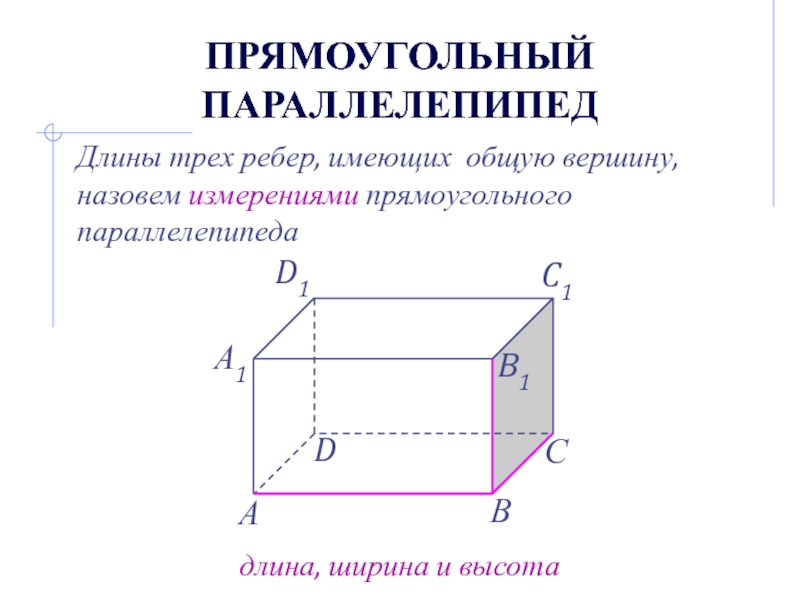
- 12. Прямоугольный параллелепипедДлины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного параллелепипедадлина, ширина и высота
- 13. Куб Прямоугольный параллелепипед, все грани которого –
- 14. Спасибо за внимание
- 15. Скачать презентанцию
Параллелепипед-четырехугольная призма, основаниями которой являются параллелограммы. Все шесть граней параллелепипеда- параллелограммы.
Слайды и текст этой презентации
Слайд 2Параллелепипед-
четырехугольная призма, основаниями которой являются параллелограммы.
Все шесть граней параллелепипеда-
параллелограммы.
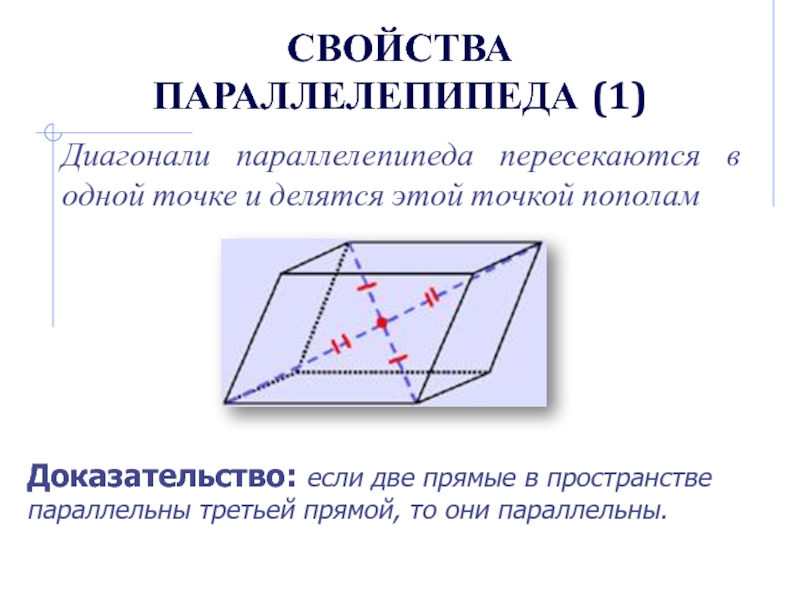
Слайд 5Свойства параллелепипеда (1)
Диагонали параллелепипеда пересекаются в одной точке и делятся
этой точкой пополам
Доказательство: если две прямые в пространстве параллельны третьей
прямой, то они параллельны.
Слайд 6 Свойства параллелепипеда (2)
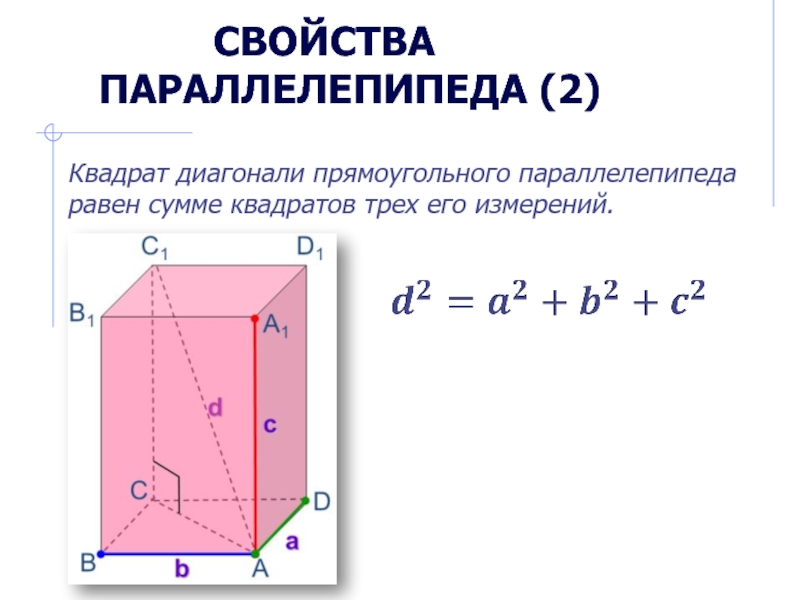
Квадрат диагонали
прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Слайд 7 Свойства параллелепипеда (3)
Объем прямоугольного
параллелепипеда равен произведению трех его измерений.
V=abc
V - объем
a - ширина
b - длина
c - высота
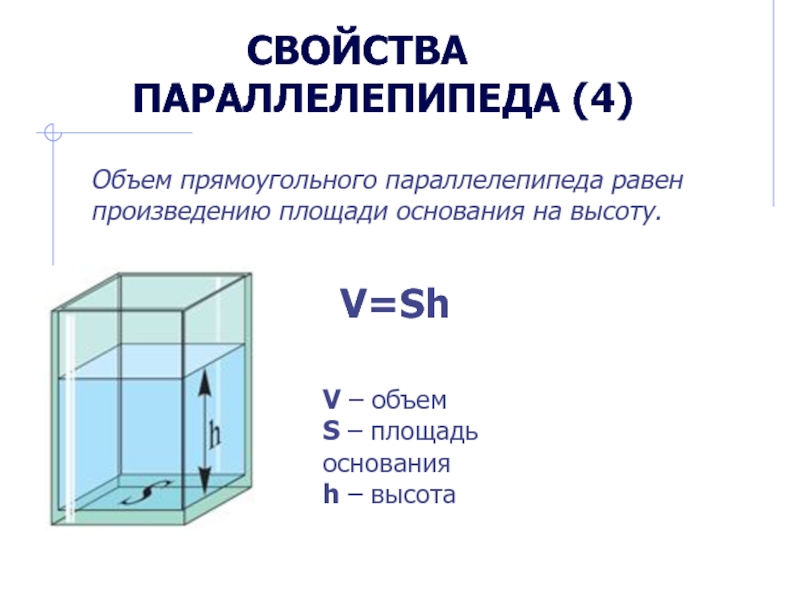
Слайд 8 Свойства параллелепипеда (4)
Объем прямоугольного
параллелепипеда равен произведению площади основания на высоту.
V=Sh
V – объем
S –
площадь основанияh – высота
Слайд 9Прямой параллелепипед
Если боковые ребра параллелепипеда перпендикулярны плоскости основания, то такой
параллелепипед называется прямым
боковые грани – прямоугольники
Слайд 10наклонный
параллелепипед
Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, относительно
оснований, под не прямым углом.
Слайд 11Прямоугольный параллелепипед
Прямой параллелепипед, основания которого являются прямоугольниками называется прямоугольным
все грани
– прямоугольники
Слайд 12Прямоугольный параллелепипед
Длины трех ребер, имеющих общую вершину, назовем измерениями прямоугольного
параллелепипеда
длина, ширина и высота
Слайд 13Куб
Прямоугольный параллелепипед, все грани которого – равные квадраты называется
кубом
все грани – равные квадраты
d2 = 3a2
d
a
a
a
