Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параллельность прямой и плоскости
Содержание
- 1. Параллельность прямой и плоскости
- 2. параллельность прямой
- 3. Аксиома 2. Если две точки прямой принадлежат
- 4. Определение. Прямая и плоскость называются параллельными, если
- 5. ГитараНатянутая гитарная струна и плоскость грифа параллельны.
- 6. Линии электропередачОни параллельны плоскости земли.
- 7. Линия пересечения стены и потолка Эта линия параллельна плоскости пола.
- 8. Теорема (Признак параллельности прямой и плоскости). Если
- 9. (Признак параллельности прямой и плоскости). Если прямая,
- 10. Утверждение 1. Если плоскость проходит через данную
- 11. Утверждение 2. Если одна из двух параллельных
- 12. Доказательство. Что и требовалось доказать.
- 13. Параллельность прямой и плоскостиПрямая и плоскость называются
- 14. Скачать презентанцию
параллельность прямой и плоскостидокажем теорему о параллельности прямой и плоскостиСегодня на уроке:докажем два утверждения, которые часто применяют при решении задач
Слайды и текст этой презентации
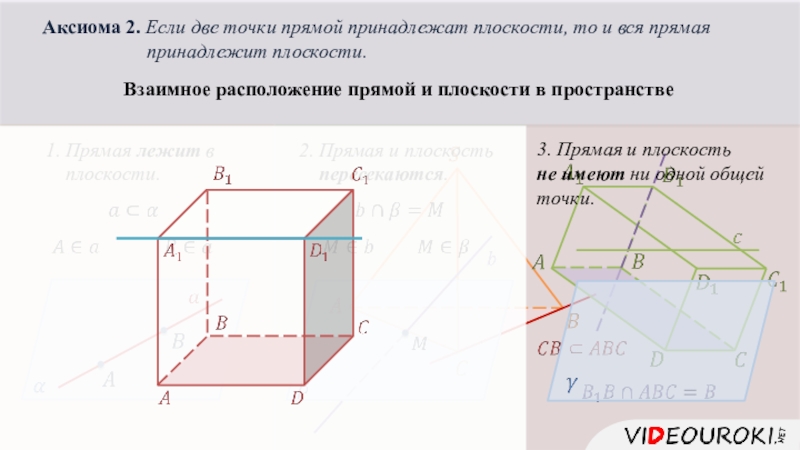
Слайд 3Аксиома 2. Если две точки прямой принадлежат плоскости, то и
вся прямая
принадлежит плоскости.Взаимное расположение прямой и плоскости в пространстве
1. Прямая лежит в
плоскости.
2. Прямая и плоскость
пересекаются.
3. Прямая и плоскость
не имеют ни одной общей точки.
Слайд 4Определение. Прямая и плоскость называются параллельными, если они не имеют
общих точек.
Определение. Отрезок (луч) называется параллельным плоскости, если он лежит
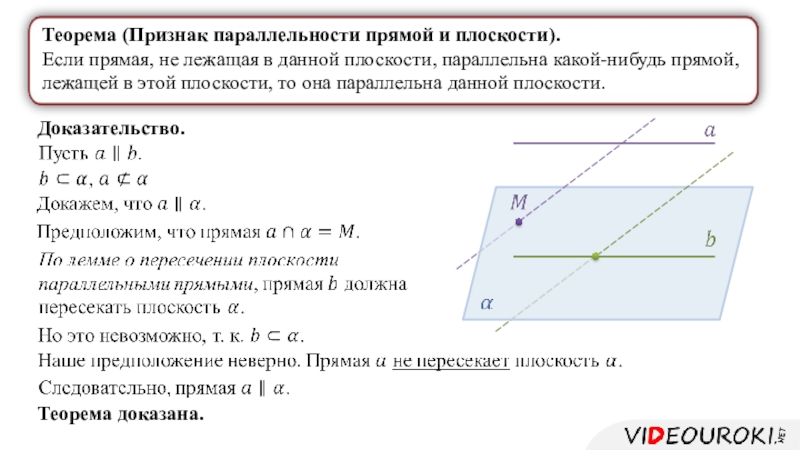
на прямой, параллельной данной плоскости.
Слайд 8Теорема (Признак параллельности прямой и плоскости).
Если прямая, не лежащая
в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости,
то она параллельна данной плоскости.Доказательство.
Теорема доказана.
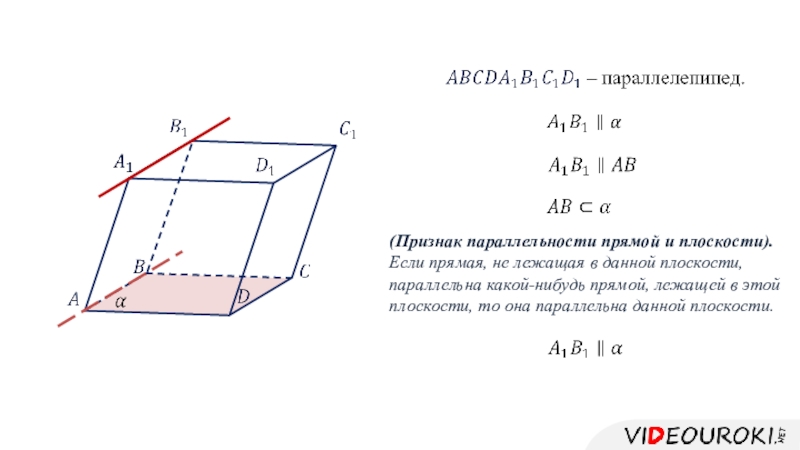
Слайд 9(Признак параллельности прямой и плоскости).
Если прямая, не лежащая в
данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то
она параллельна данной плоскости.
Слайд 10Утверждение 1. Если плоскость проходит через данную прямую, параллельную другой
плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна
данной прямой.Доказательство.
Что и требовалось доказать.
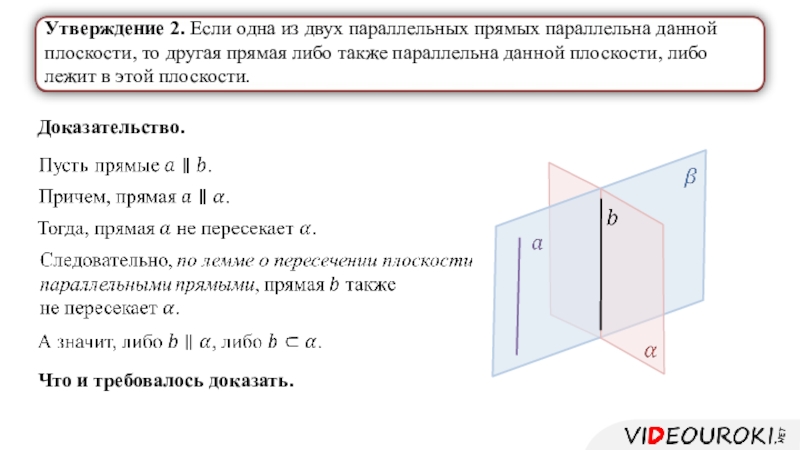
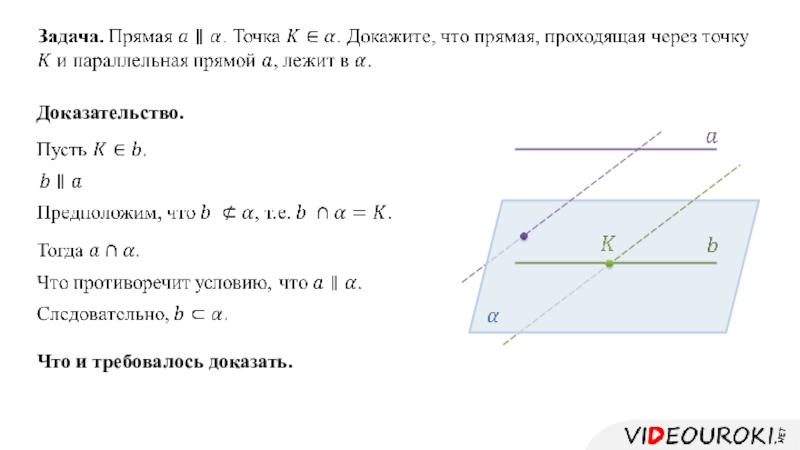
Слайд 11Утверждение 2. Если одна из двух параллельных прямых параллельна данной
плоскости, то другая прямая либо также параллельна данной плоскости, либо
лежит в этой плоскости.Доказательство.
Что и требовалось доказать.
Слайд 13Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они
не имеют общих точек.
Теорема (Признак параллельности прямой и плоскости).
Если
прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.Утверждение 1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Утверждение 2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
