ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

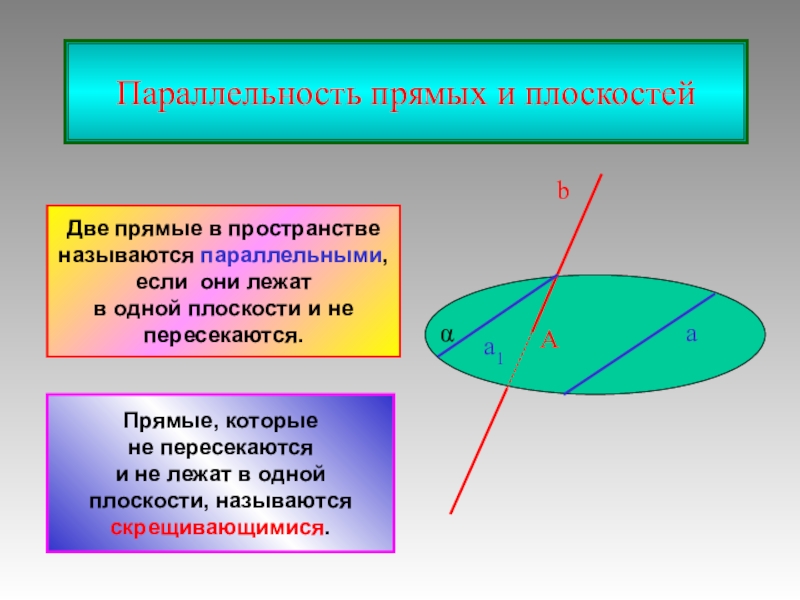
они лежат
в одной плоскости и не
пересекаются.
a1
Прямые, которые
не пересекаются
и

точку вне
данной прямой можно провести
прямую, параллельную этой
прямой, и притом только

а

А

собой.
а
b
c

М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1,

•

А

В

М

А1

В1

М1

Решение: Т.к. АА1 и ВВ1 параллельны между собой, то четырёхугольник А1АВВ1- трапеция.

ММ1 – средняя линия трапеции.

ММ1 = (АА1 + ВВ1) / 2 = ( 5 + 7 ) : 2 = 6 (м)

Ответ: 6 м.

5

7

Прямая и плоскость называются параллельными, если они не пересекаются.
Теорема 2.3

a

b

Дано: a b, b

а1

Доказать: a

M

Признак параллельности прямой и плоскости

пересекает её по прямой, параллельной данной прямой.
a
b
Дано: a

а1

Доказать: b a

M

АВ, пересекает сторону АС этого треугольника в точке А1, а

А

В

С

А1

В1

Решение: треугольник АВС подобен треугольнику А1В1С. Поэтому составим пропорцию

т.е. не имеют общих точек.
Теорема 2.4. Если две пересекающие
прямые

a1

a2

b1

b2

A

•

c

плоскости можно провести плоскость,
параллельную данной, притом
только одну .

•
a
b
A

третьей,
то прямые пересечения параллельны
между собой.
a
b

двумя
параллельными плоскостями равны.
a
b
A1
A2
B1
B2