Парная регрессия и корреляция

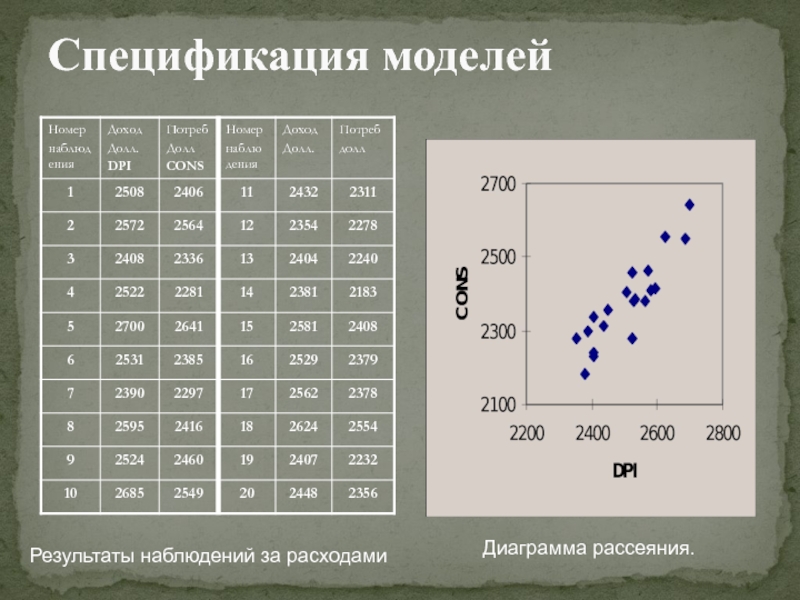
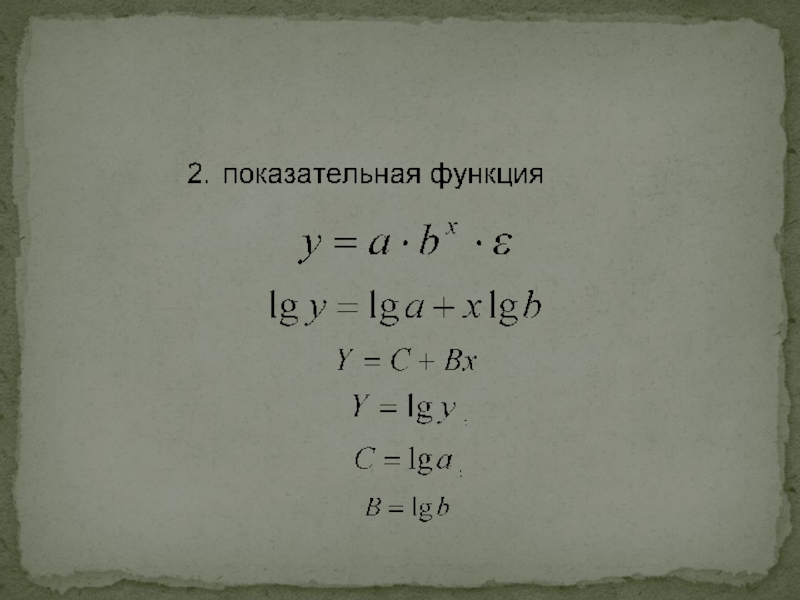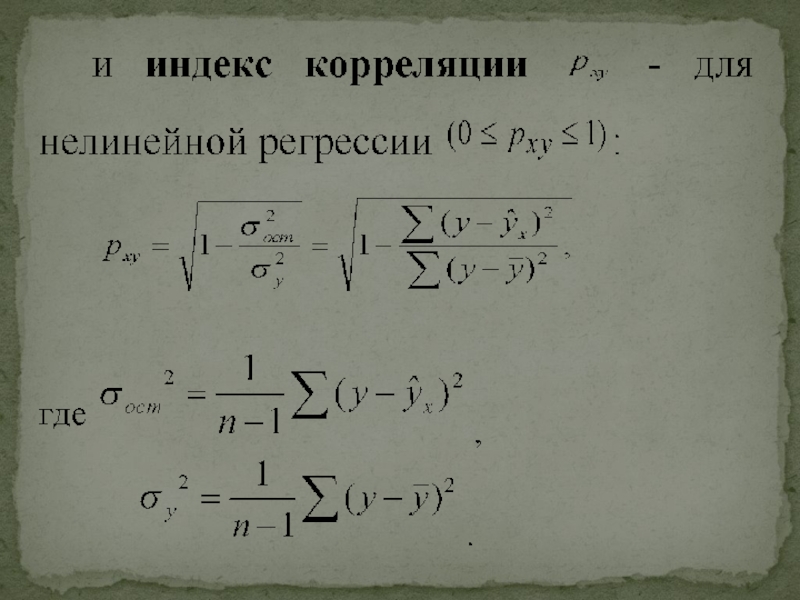понятия «экономическая величина»;
Формированием системы принципов, постулатов и других теоретических положений,

формирующих базис точности экономических измерений;
Определением экономических показателей;
Разработкой принципов конструирования измерителей и измерений;
Основанием выбора типа шкал при конструировании измерителя;
Разработкой правил формирования систем показателей;
Выявлением типов и определением методов устранения ошибок экономического измерения;
Разработкой правил агрегирования и сверки экономических показателей;
Выявлением условий сравнимости экономических величин (показателей);
Разработкой правил и методов измерений.

хозяйств
Влияние неучтенных факторов.
Выводы:
Невозможно построить модель вида Y=f(x), с помощью

которой возможно однозначно определить связь между расходами и доходами.
Зависимость между доходами и расходами домашних хозяйств имеет элемент случайности.

Спецификация моделей

= f(X) + ε
где: Y – эндогенная переменная;

X – вектор предопределенных переменных;
f(X) – детерминированная математическая функция, определяющая закономерность между эндогенной и предопределенными переменными;
ε – случайная величина, учитывающая влияние неучтенных факторов и индивидуальные особенности конкретного объекта.

(результативный признак);
x – независимая, объясняющая переменная (признак-фактор)

Парная регрессия

в анализ объясняющих переменных, но линейные по оцениваемым параметрам;
Регрессии, нелинейные

по оцениваемым параметрам

Различают линейные и нелинейные регрессии

двумя количественными переменными х и у, представленная уравнением y =

a + bx

из них, b представляет собой величину, на которую изменяется предсказанное

по модели значение ŷi = a + bxi при увеличении значения независимой переменной x на одну единицу измерения, согласно второй - величину, на которую в среднем изменяется значение переменной yi при увеличении независимой переменной x на единицу.
На диаграмме рассеяния коэффициент b представляет тангенс угла наклона линии регрессии y = a + bx к оси абсцисс. Знак коэффициента регрессии совпадает со знаком коэффициента линейной корреляции: значение b > 0 свидетельствует о прямой линейной связи, значение b < 0 - об обратной. Если b = 0, линейная связь между переменными отсутствует (линия регрессии параллельна оси абсцисс).

значение x = 0 имеет смысл. В этом случае y

= a, если x = 0.

квадратов (МНК).
МНК позволяет получить такие оценки параметров, при которых сумма

квадратов отклонений фактических значений результативного признака y от теоретических минимальна, то есть

Построение уравнения регрессии сводится к оценке ее параметров

система относительно a и b:


:

критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть

для определения значимых различий между групповыми средними в установке дисперсионного анализа.

F-критерий Фишера

из распределения с неизвестным параметром, такой, что он накрывает данный

параметр с заданной вероятностью.

работы.

Желаю удачи!