PDMKVVSNAS CTTNCLAPLA
human GAKRVIISAP SAD.APM..F VMGVNHEKYD NSLKIISNAS CTTNCLAPLA
plant GAKKVIISAP SAD.APM..F VVGVNEHTYQ PNMDIVSNAS CTTNCLAPLA
bacterium GAKKVVMTGP SKDNTPM..F VKGANFDKY. AGQDIVSNAS CTTNCLAPLA
yeast GAKKVVITAP SS.TAPM..F VMGVNEEKYT SDLKIVSNAS CTTNCLAPLA
archaeon GADKVLISAP PKGDEPVKQL VYGVNHDEYD GE.DVVSNAS CTTNSITPVA
fly KVINDNFEIV EGLMTTVHAT TATQKTVDGP SGKLWRDGRG AAQNIIPAST
human KVIHDNFGIV EGLMTTVHAI TATQKTVDGP SGKLWRDGRG ALQNIIPAST
plant KVVHEEFGIL EGLMTTVHAT TATQKTVDGP SMKDWRGGRG ASQNIIPSST
bacterium KVINDNFGII EGLMTTVHAT TATQKTVDGP SHKDWRGGRG ASQNIIPSST
yeast KVINDAFGIE EGLMTTVHSL TATQKTVDGP SHKDWRGGRT ASGNIIPSST
archaeon KVLDEEFGIN AGQLTTVHAY TGSQNLMDGP NGKP.RRRRA AAENIIPTST
fly GAAKAVGKVI PALNGKLTGM AFRVPTPNVS VVDLTVRLGK GASYDEIKAK
human GAAKAVGKVI PELNGKLTGM AFRVPTANVS VVDLTCRLEK PAKYDDIKKV
plant GAAKAVGKVL PELNGKLTGM AFRVPTSNVS VVDLTCRLEK GASYEDVKAA
bacterium GAAKAVGKVL PELNGKLTGM AFRVPTPNVS VVDLTVRLEK AATYEQIKAA
yeast GAAKAVGKVL PELQGKLTGM AFRVPTVDVS VVDLTVKLNK ETTYDEIKKV
archaeon GAAQAATEVL PELEGKLDGM AIRVPVPNGS ITEFVVDLDD DVTESDVNAA
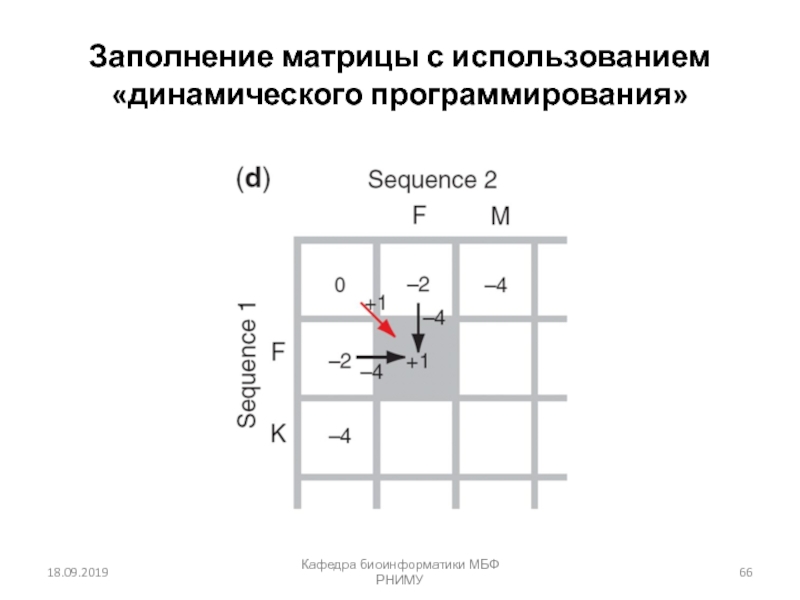
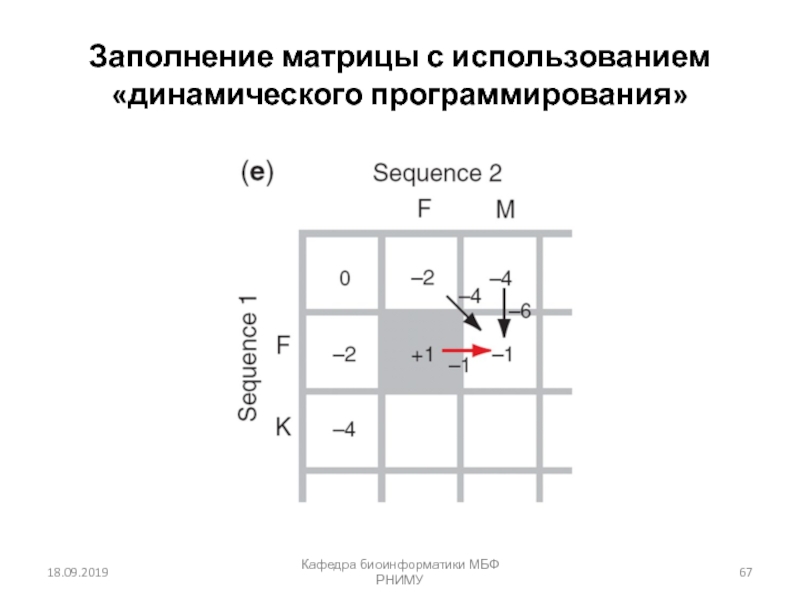
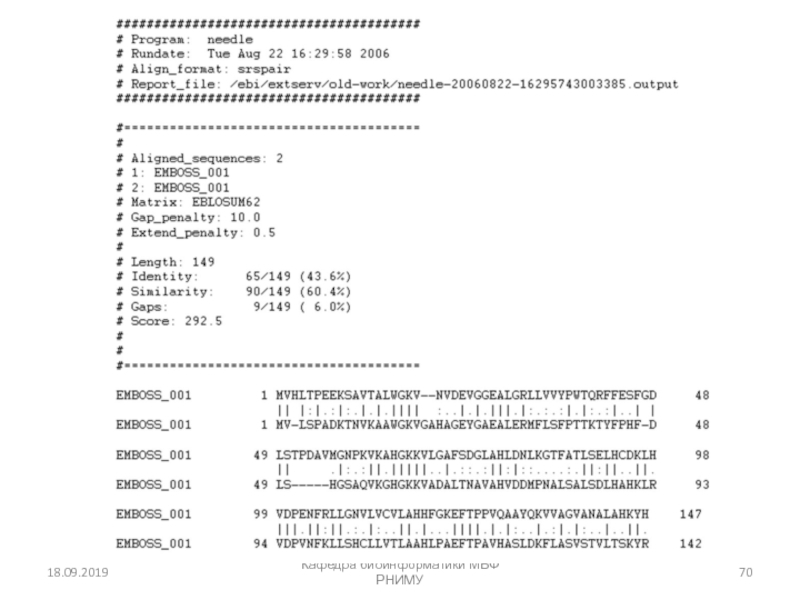
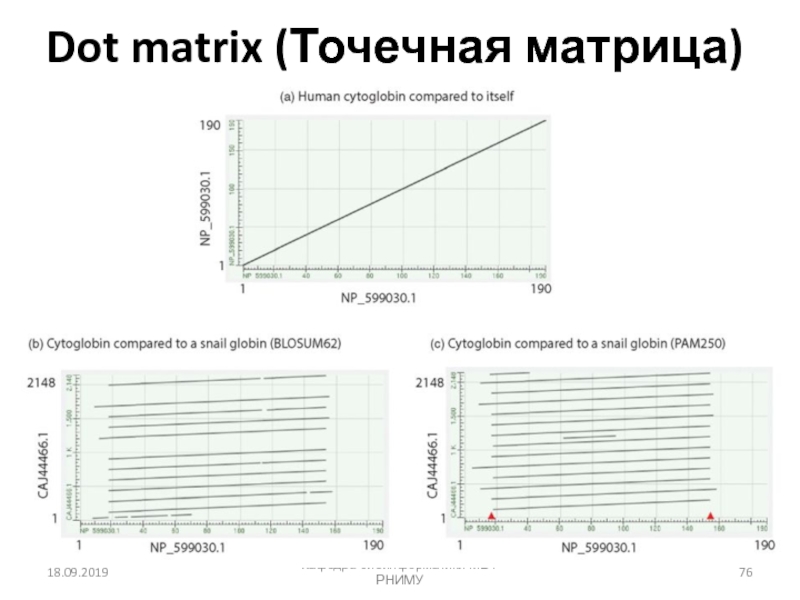
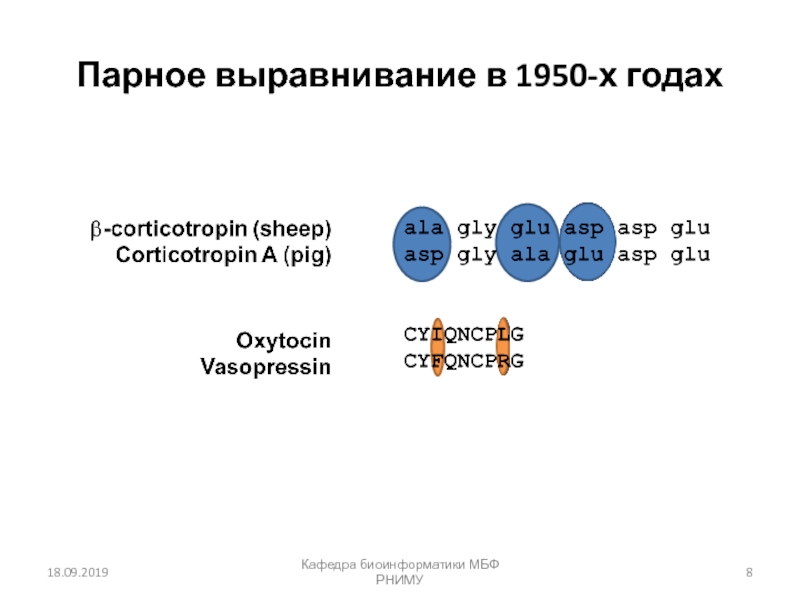
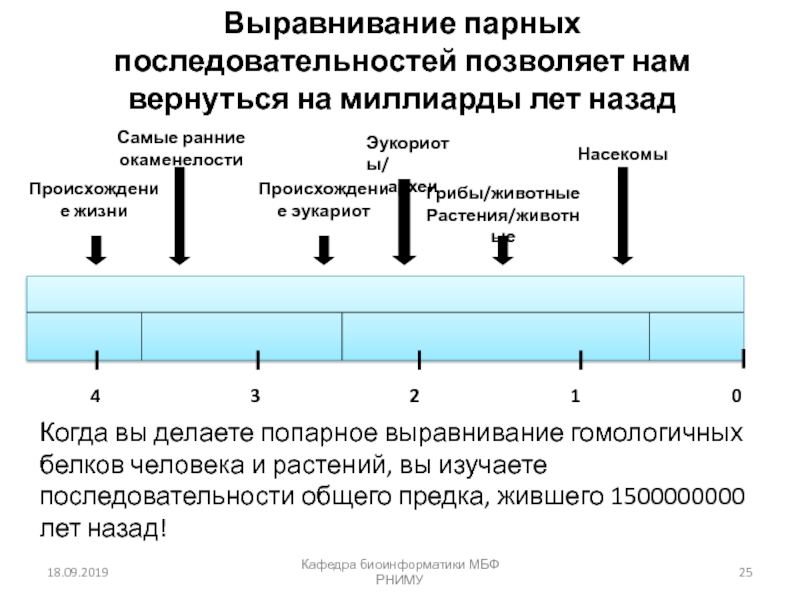
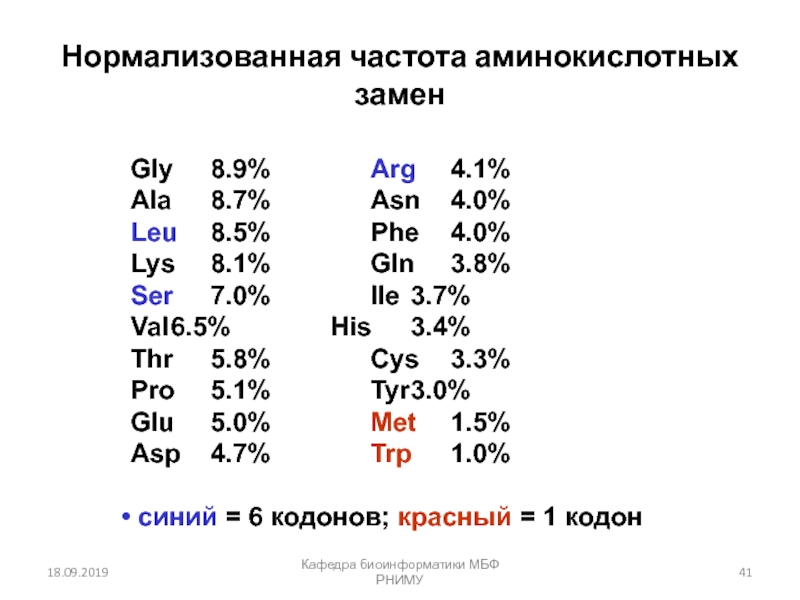
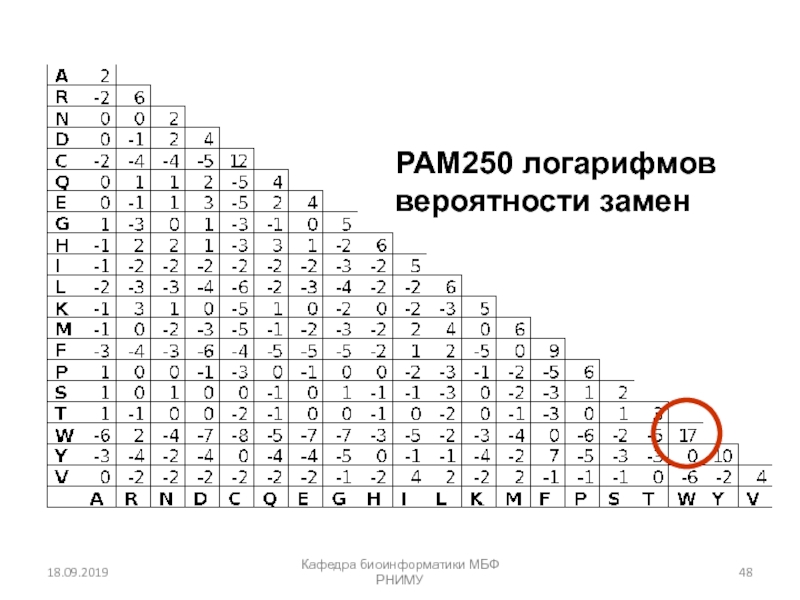
Множественное выравнивание последовательностей
глицеральдегид 3-фосфат дегидрогеназ:
пример очень высокого консерватизма

































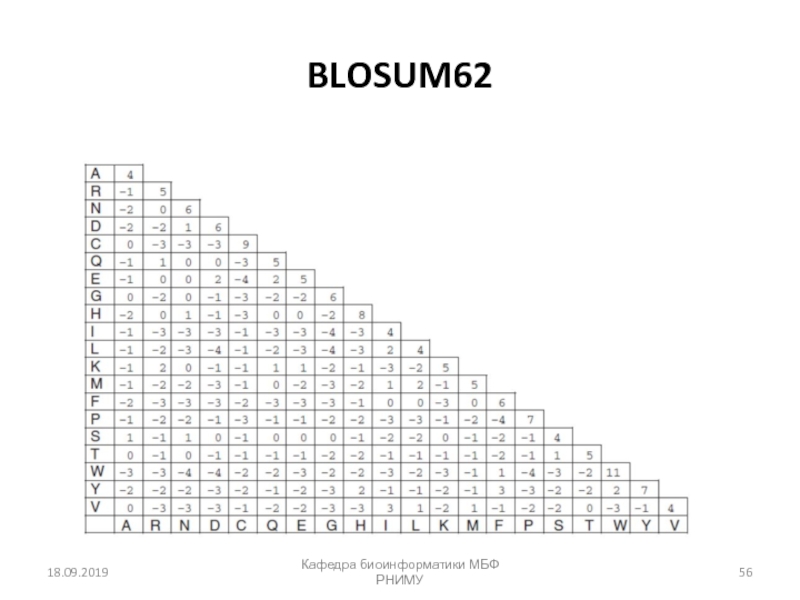
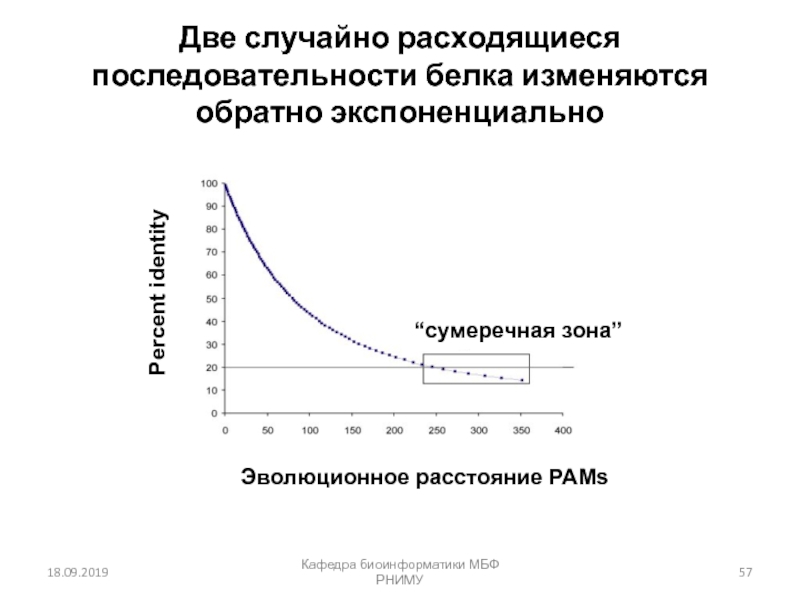



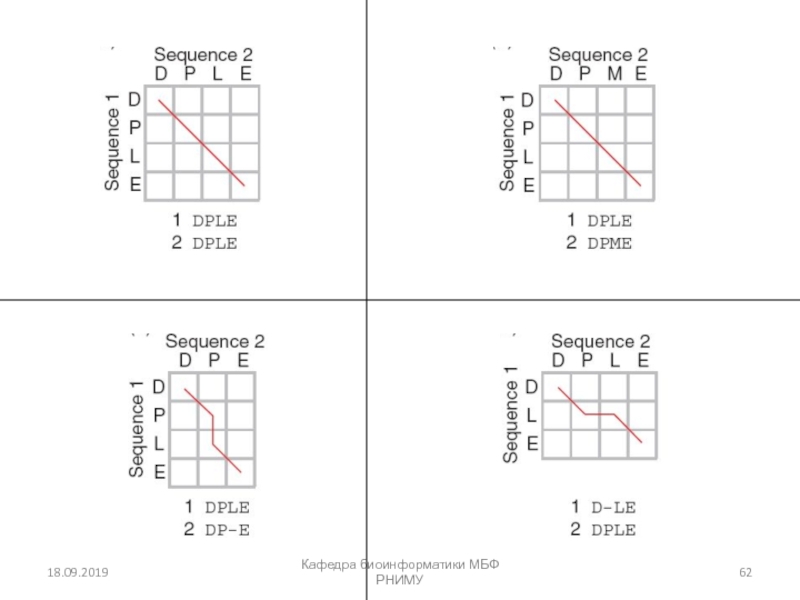
![Парное выравнивание. Матрицы замен. BLAST Четыре возможных исхода при выравнивании двух последовательностейКафедра биоинформатики МБФ РНИМУ[1] идентичность Четыре возможных исхода при выравнивании двух последовательностейКафедра биоинформатики МБФ РНИМУ[1] идентичность (оставаться вдоль диагонали)[2] несовпадение](/img/thumbs/37c5b213ba9dc6452541d833c322ac69-800x.jpg)