Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересечение поверхностей. Способ вспомогательных концентрических сфер
Содержание
- 1. Пересечение поверхностей. Способ вспомогательных концентрических сфер
- 2. ОСНОВНОЙ ПРИНЦИПСфера с поверхностями вращения оси
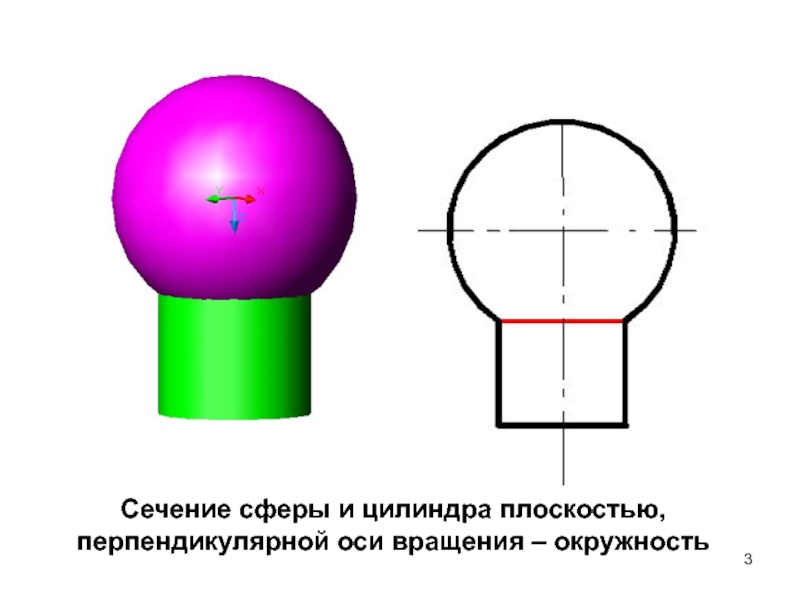
- 3. Сечение сферы и цилиндра плоскостью, перпендикулярной оси вращения – окружность
- 4. УСЛОВИЯ при которых задачу можно решать способом
- 5. Пересечение конуса и цилиндра
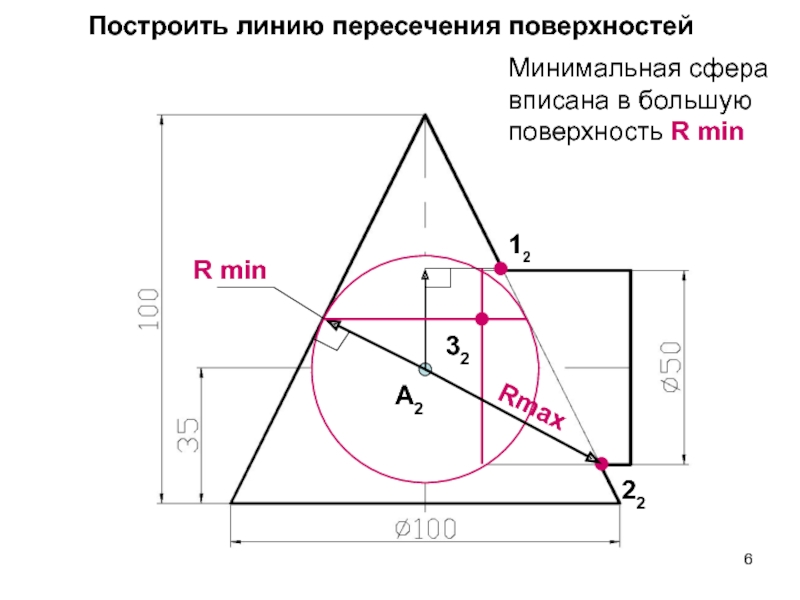
- 6. Построить линию пересечения поверхностейА2Минимальная сфера вписана в большую поверхность R minR min321222Rmax
- 7. 42
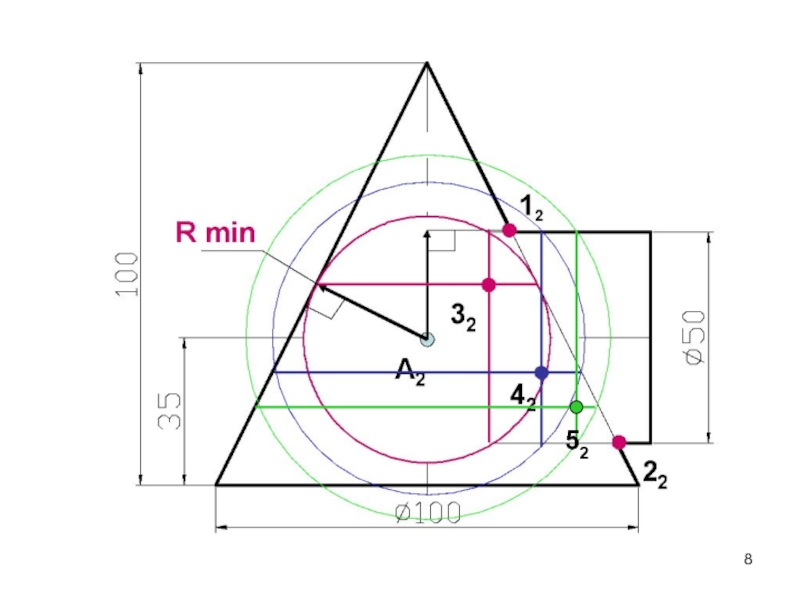
- 8. 52
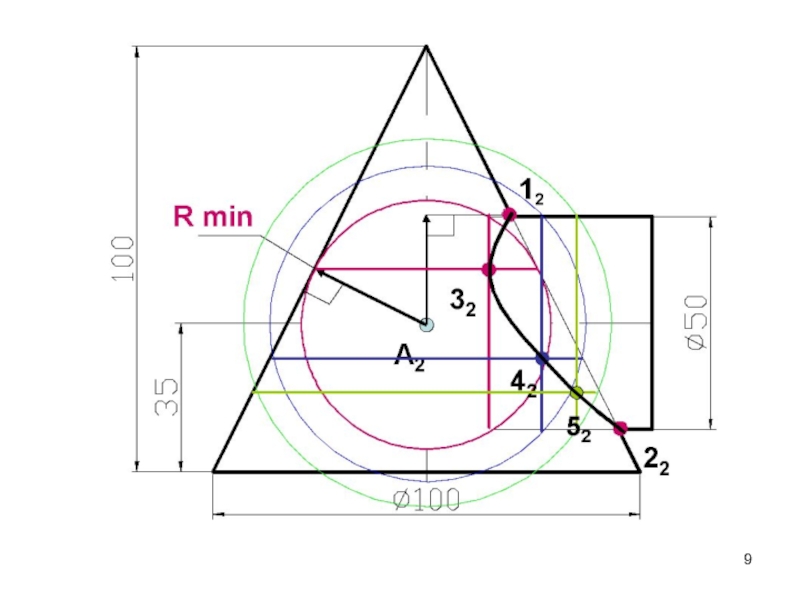
- 9. Слайд 9
- 10. ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ЦИЛИНДРЫ С ПАРАЛЛЕЛЬНЫМИ ОСЯМИ пересекаются по образующим (2 прямые линии)11212212
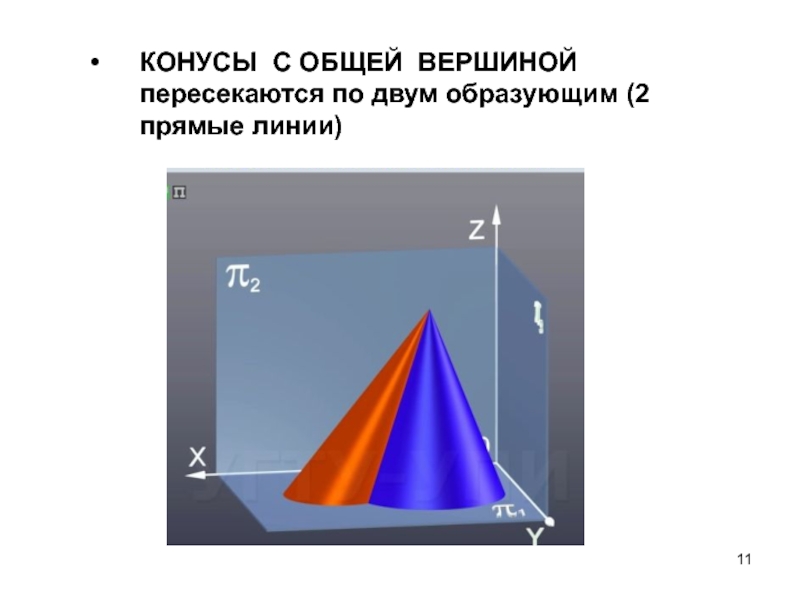
- 11. КОНУСЫ С ОБЩЕЙ ВЕРШИНОЙ пересекаются по двум образующим (2 прямые линии)
- 12. ЕСЛИ ДВЕ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- 13. Слайд 13
- 14. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, ИМЕЮЩИЕ ДВЕ ТОЧКИ КАСАНИЯ,
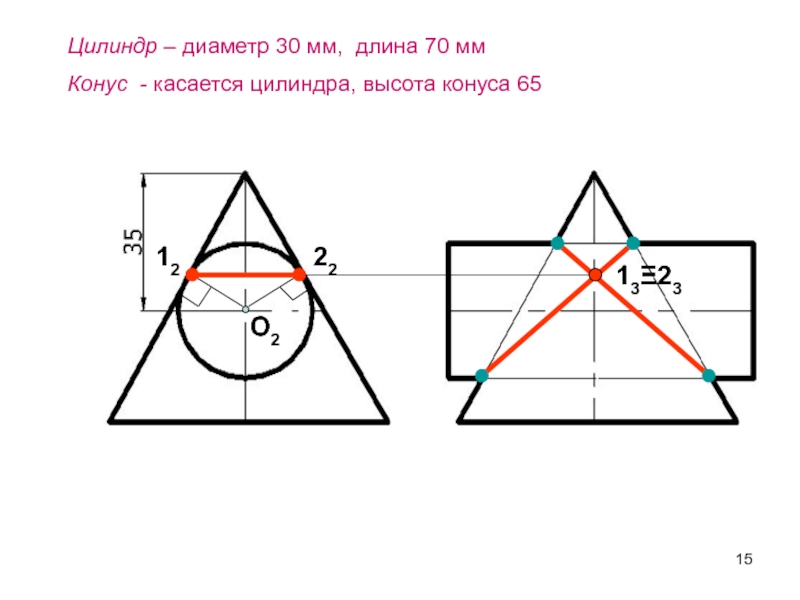
- 15. Цилиндр – диаметр 30 мм, длина 70 ммКонус - касается цилиндра, высота конуса 65О2122213Ξ23
- 16. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ОПИСАННЫЕ ИЛИ ВПИСАННЫЕ
- 17. Поверхность второго порядка – сфера
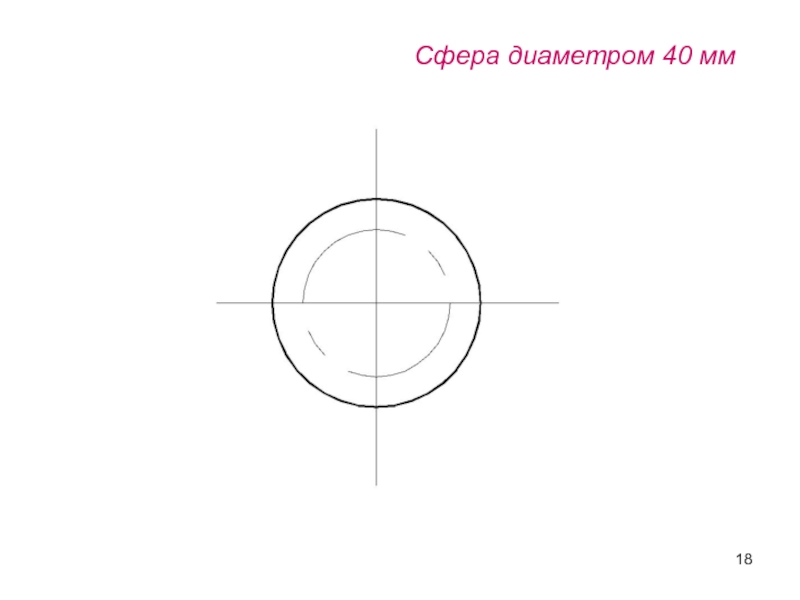
- 18. Сфера диаметром 40 мм
- 19. Слайд 19
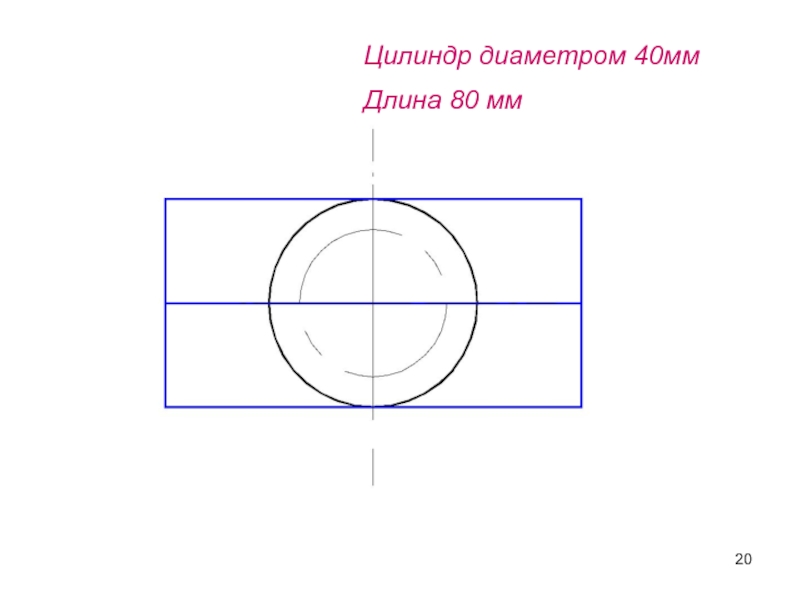
- 20. Цилиндр диаметром 40ммДлина 80 мм
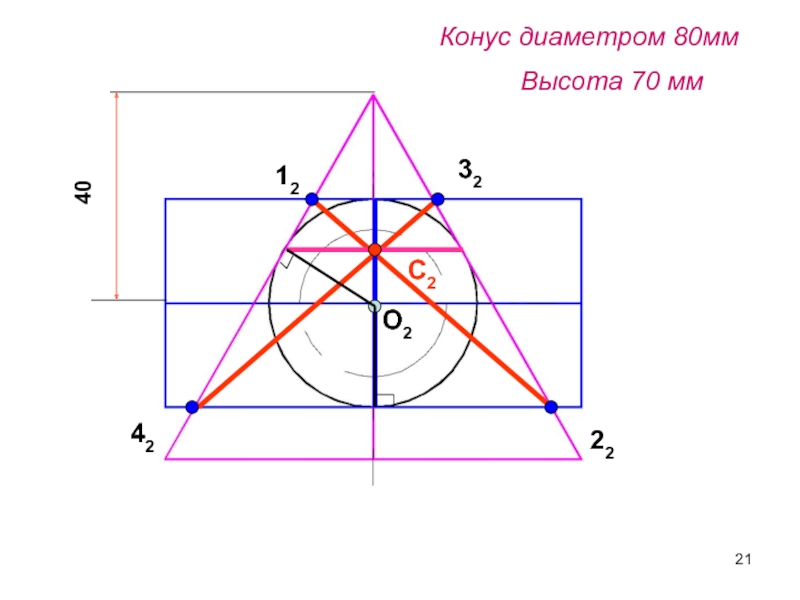
- 21. Конус диаметром 80мм Высота 70 мм40С212223242О2
- 22. Построить линию пересечения поверхностей
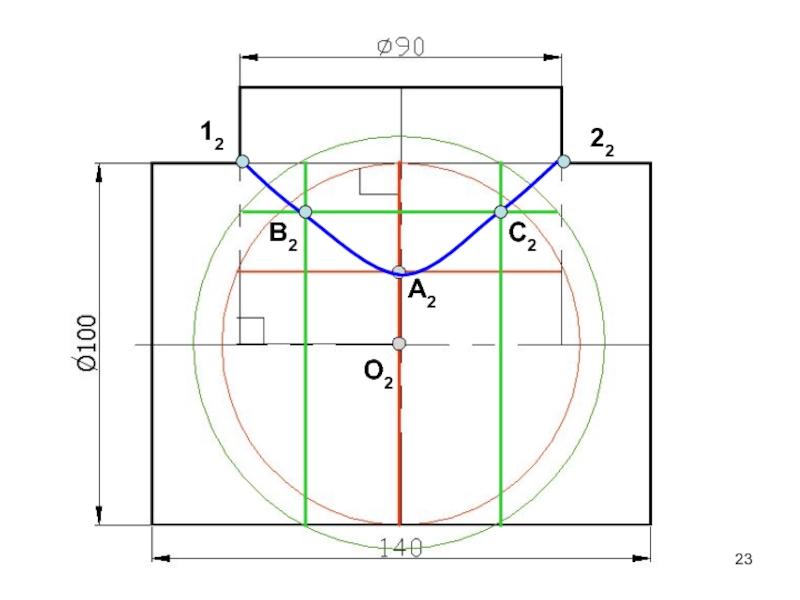
- 23. О2А2В2С21222
- 24. Скачать презентанцию
ОСНОВНОЙ ПРИНЦИПСфера с поверхностями вращения оси которых проходят через ЦЕНТР СФЕРЫ, пересекается по окружностям, плоскости которых перпендикулярны оси вращения поверхности
Слайды и текст этой презентации
Слайд 1Пересечение поверхностей. Способ вспомогательных концентрических сфер
Построение линий пересечения поверхностей способом
вспомогательных концентрических сфер
Слайд 2ОСНОВНОЙ ПРИНЦИП
Сфера с поверхностями вращения оси которых проходят через
ЦЕНТР СФЕРЫ, пересекается по окружностям, плоскости которых перпендикулярны оси вращения
поверхности
Слайд 4УСЛОВИЯ при которых задачу можно решать способом концентрических сфер
1. ПЕРЕСЕКАЮТСЯ
ПОВЕРХНОСТИ ВРАЩЕНИЯ
ОСИ ВРАЩЕНИЯ ПОВЕРХНОСТЕЙ
ПЕРЕСЕКАЮТСЯ
ПОВЕРХНОСТИ
ИМЕЮТ ОБЩУЮ ПЛОСКОСТЬСИММЕТРИИ
Слайд 6Построить линию пересечения поверхностей
А2
Минимальная сфера вписана в большую поверхность R
min
R min
32
12
22
Rmax
Слайд 10ЧАСТНЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
ЦИЛИНДРЫ С ПАРАЛЛЕЛЬНЫМИ ОСЯМИ пересекаются по
образующим (2 прямые линии)
11
21
22
12
Слайд 12 ЕСЛИ ДВЕ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ПЕРЕСЕКАЮТСЯ ПО ОДНОЙ
ПЛОСКОЙ КРИВОЙ, ТО ЕСТЬ И ВТОРАЯ ПЛОСКАЯ
КРИВАЯ ПО КОТОРОЙ ОНИ ПЕРЕСЕКАЮТСЯ
Слайд 14ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, ИМЕЮЩИЕ ДВЕ ТОЧКИ КАСАНИЯ, ПЕРЕСЕКАЮТСЯ ПО ДВУМ
КРИВЫМ ВТОРОГО ПОРЯДКА, ПЛОСКОСТИ КОТОРЫХ ПРОХОДЯТ ЧЕРЕЗ ПРЯМУЮ, СОЕДИНЯЮЩУЮ ТОЧКИ
КАСАНИЯ ПОВЕРХНОСТЕЙ
Слайд 16ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА ОПИСАННЫЕ ИЛИ ВПИСАННЫЕ В ДРУГУЮ ПОВЕРХНОСТЬ
2 ПОРЯДКА, ПЕРЕСЕКАЮТСЯ ПО ДВУМ КРИВЫМ ВТОРОГО ПОРЯДКА, ПЛОСКОСТИ КОТОРЫХ
ПРОХОДЯТ ЧЕРЕЗ ПРЯМУЮ, СОЕДИНЯЮЩУЮ ТОЧКИ ПЕРЕСЕЧЕНИЯ ЛИНИЙ КАСАНИЯ
