Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересечение поверхности плоскостью
Содержание
- 1. Пересечение поверхности плоскостью
- 2. Форма линии пересечения поверхности плоскостью определяется формой
- 3. Σ ∩ Ф = aФ{m1,
- 4. Количество точек, используемых для постро-ения линии пересечения,
- 5. В общем случае решение задачи на построение
- 6. Данная коническая поверхность относится к классу линейчатых
- 7. В общем случае решение задачи на построение
- 8. Слайд 8
- 9. Пересечение конической поверхности плоскостью
- 10. При пересечении прямой круговой конической поверхности плоскостью
- 11. Ф – прямая круговая коническая
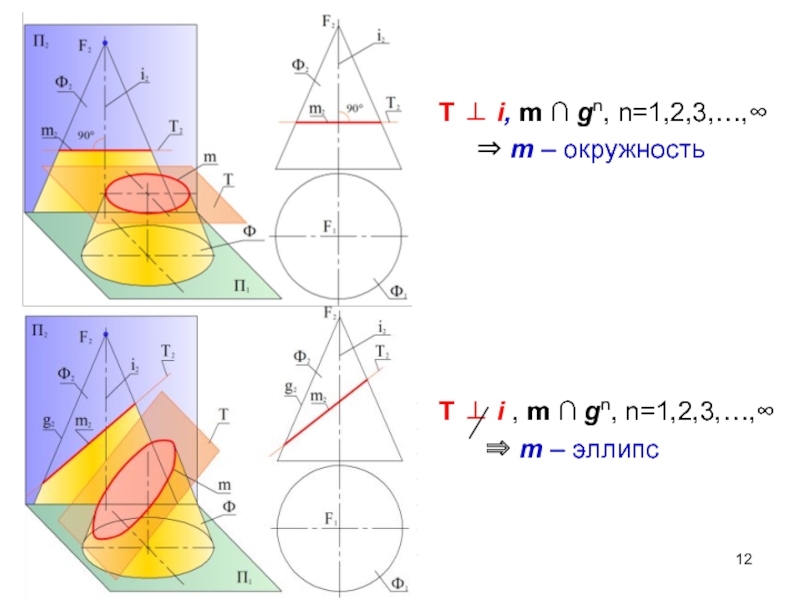
- 12. T ⊥ i, m ∩ gn, n=1,2,3,…,
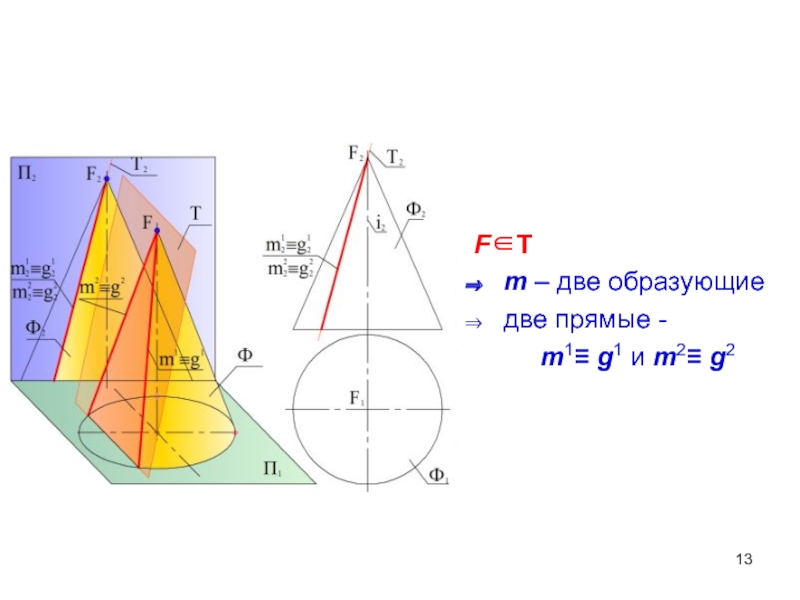
- 13. FT m – две образующие две прямые
- 14. T II g m –
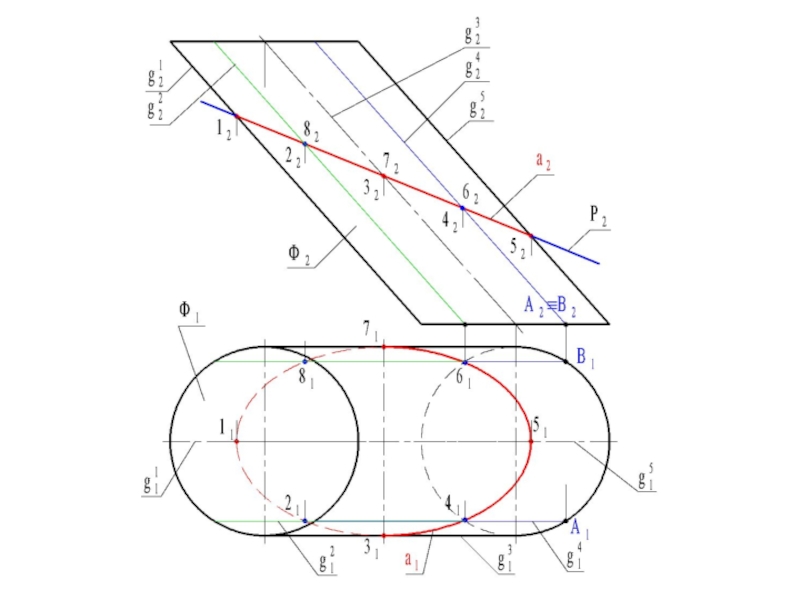
- 15. Пересечение цилиндрической поверхности плоскостью
- 16. Ф – прямая круговая цилиндрическая
- 17. Форма линии пересечения прямой круго-вой цилиндрической поверхности
- 18. T ⊥ i, m ∩
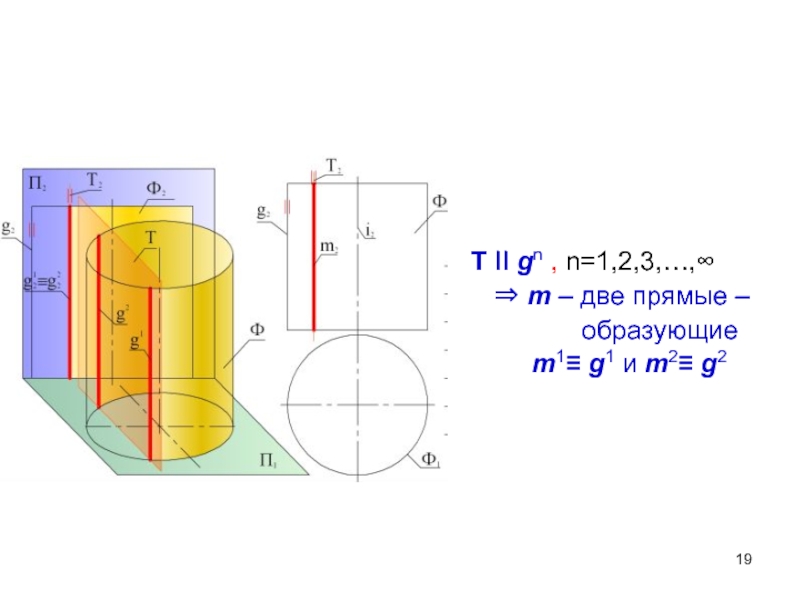
- 19. Т II gn , n=1,2,3,…,
- 20. Пересечение гранной поверхности плоскостью
- 21. При пересечении гранной поверхности плоскостью линия пересечения
- 22. Количество используемых точек линии пересечения плоскости с
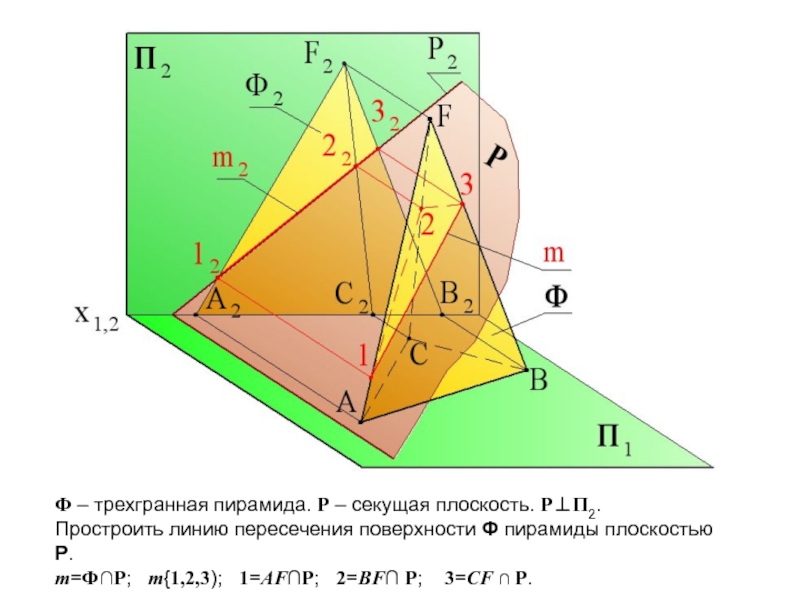
- 23. Ф – трехгранная пирамида. Р – секущая
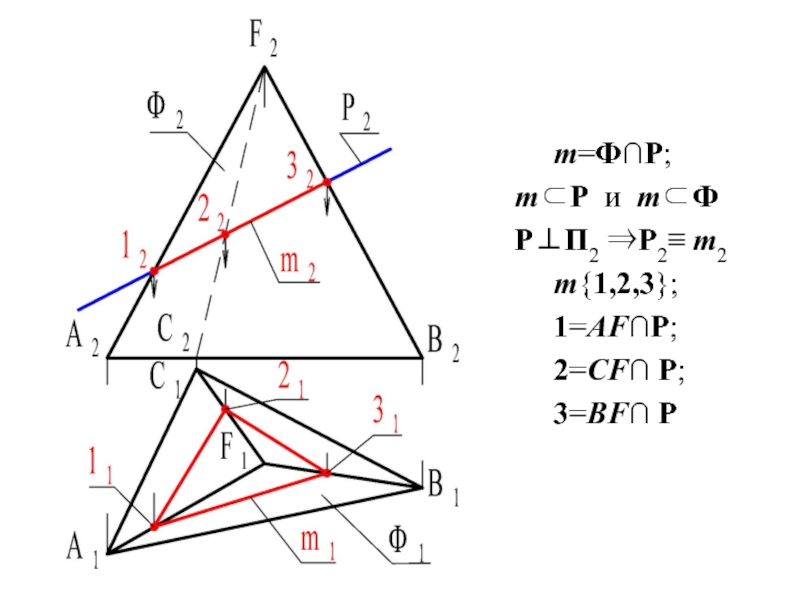
- 24. m=Ф∩Р; mP и
- 25. Скачать презентанцию
Форма линии пересечения поверхности плоскостью определяется формой заданной поверхности и положением плоскости относительно этой поверхности.Для кривой поверхности, в общем случае, линия пересечения - это плоская кривая линия.
Слайды и текст этой презентации
Слайд 2Форма линии пересечения поверхности плоскостью определяется формой заданной поверхности и
положением плоскости относительно этой поверхности.
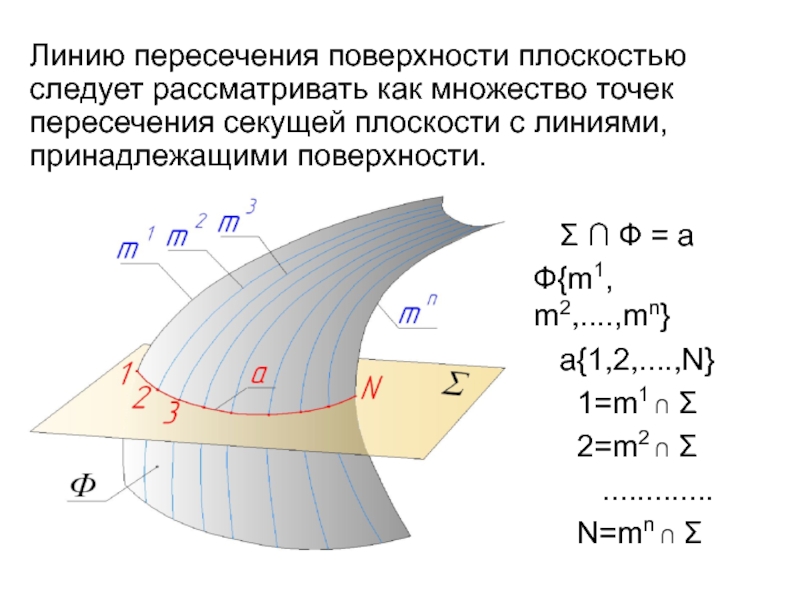
линия пересечения - это плоская кривая линия.Слайд 3 Σ ∩ Ф = a
Ф{m1, m2,....,mn}
a{1,2,....,N}
1=m1 ∩ Σ
2=m2 ∩ Σ
.............N=mn ∩ Σ
Линию пересечения поверхности плоскостью следует рассматривать как множество точек пересечения секущей плоскости с линиями, принадлежащими поверхности.
Слайд 4Количество точек, используемых для постро-ения линии пересечения, определяется фор-мой поверхности
и точностью построения.
Но из всего множества точек линии пересечения обязательно
должны быть построены следующие точки:точки, определяющие габариты фигуру сечения;
точки фигуры сечения наиболее и наиме-нее удаленные от плоскостей проекций;
точки, определяющие видимость фигуры сечения на проекциях.
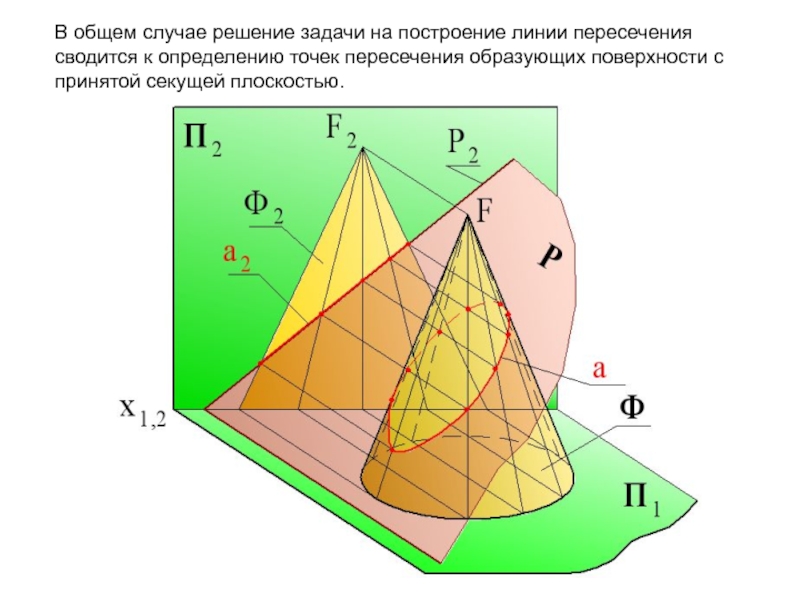
Слайд 5В общем случае решение задачи на построение линии пересечения сводится
к определению точек пересечения образующих поверхности с принятой секущей плоскостью.
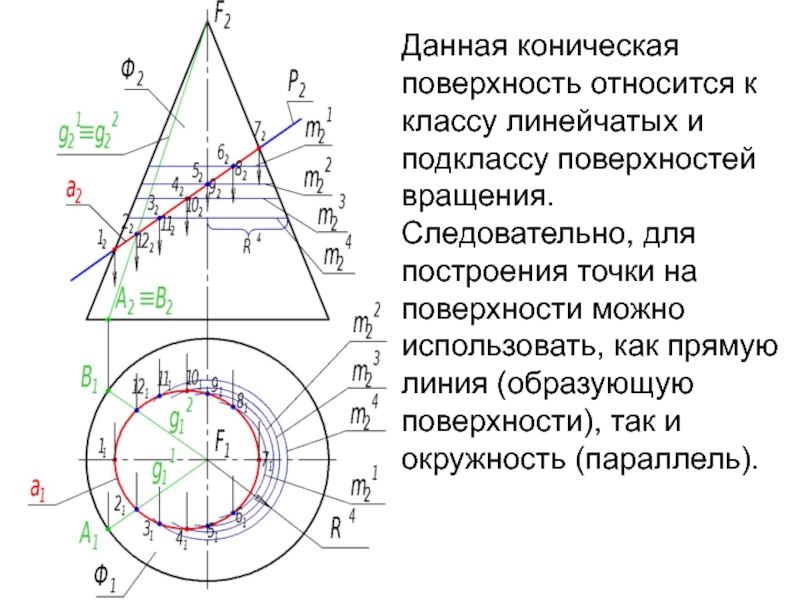
Слайд 6Данная коническая поверхность относится к классу линейчатых и подклассу поверхностей
вращения. Следовательно, для построения точки на поверхности можно использовать, как
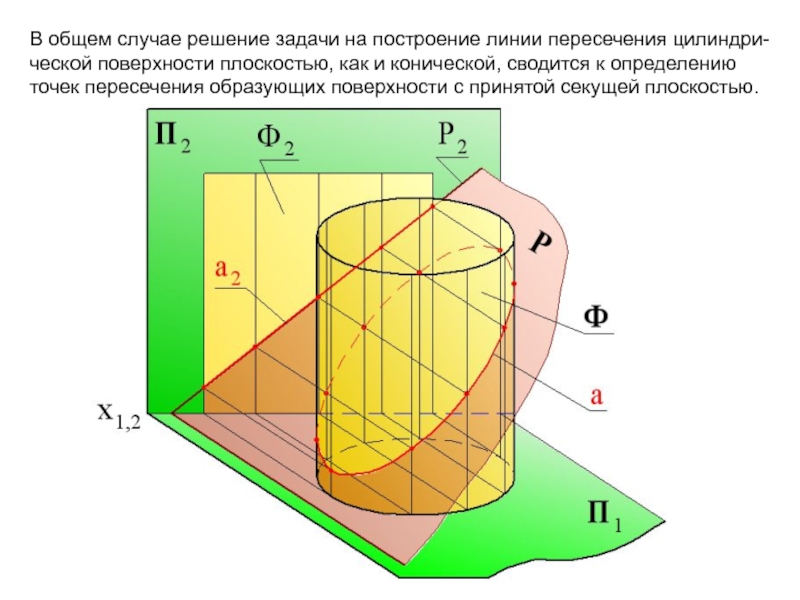
прямую линия (образующую поверхности), так и окружность (параллель).Слайд 7В общем случае решение задачи на построение линии пересечения цилиндри-ческой
поверхности плоскостью, как и конической, сводится к определению точек пересечения
образующих поверхности с принятой секущей плоскостью.Слайд 10При пересечении прямой круговой конической поверхности плоскостью форма линии пересечения
определяется не только формой самой поверхности, но и положением секущей
плоскости относительно отдельных элементов поверхности – вершины, оси вращения, образующих.Слайд 11Ф – прямая круговая коническая
поверхность.
Т
– секущая плоскость.
Ф ∩ Т = m,
m – линия
пересеченияСлайд 16Ф – прямая круговая цилиндрическая
поверхность.
Т
– секущая плоскость.
Ф ∩ Т = m,
m – линия
пересеченияСлайд 17Форма линии пересечения прямой круго-вой цилиндрической поверхности плоскос-тью, так же
как и при пересечении прямой круговой конической поверхности, опреде-ляется положением
секущей плоскости отно-сительно отдельных элементов поверхности – оси вращения и образующих.Слайд 21При пересечении гранной поверхности плоскостью линия пересечения – это ломаная
линия, каждый участок которой – отрезок прямой, представляющий собой линию
пересечения грани поверхности (отсека плоскости) с секущей плоскостью, а точки излома – точки пересечения ребер гранной поверхности (отрезков прямых) с той же секущей плоскостью.Следовательно, решение задачи на построение линии пересечения сводится к определению точек пересечения ребер гранной поверхности с принятой секущей плоскостью.