Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
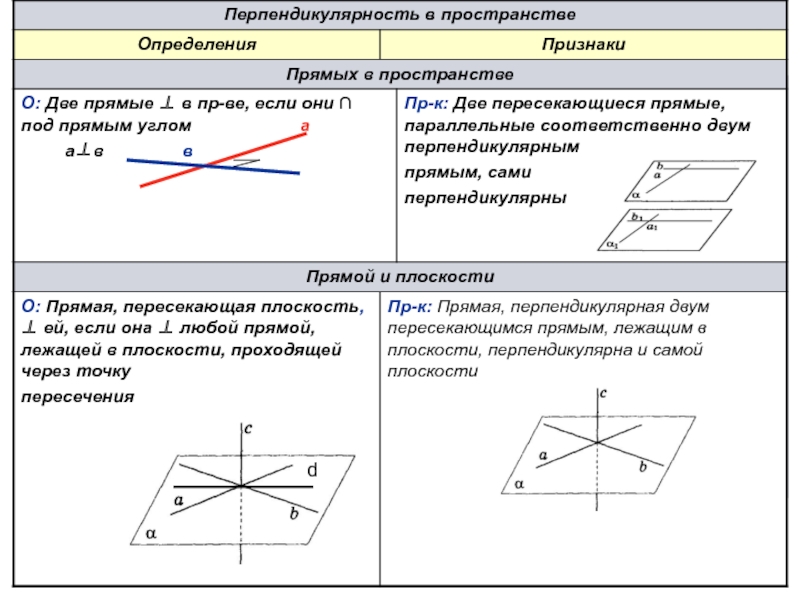
Перпендикулярность в пространстве
Содержание
- 1. Перпендикулярность в пространстве
- 2. d
- 3. 1.Плоскость, перпендикулярная одной из двух параллельных прямых,перпендикулярна
- 4. α=с, с, =а, =в, ав, (b α, b β) α β
- 5. Если плоскости перпендикулярны, то прямая лежащая в
- 6. Перпендикуляр и наклоннаяПерпендикуляр АВНаклонная АСпроекция АС на пл-ть AD=AB DC=CDАВ > AC AC>AD CB>BD
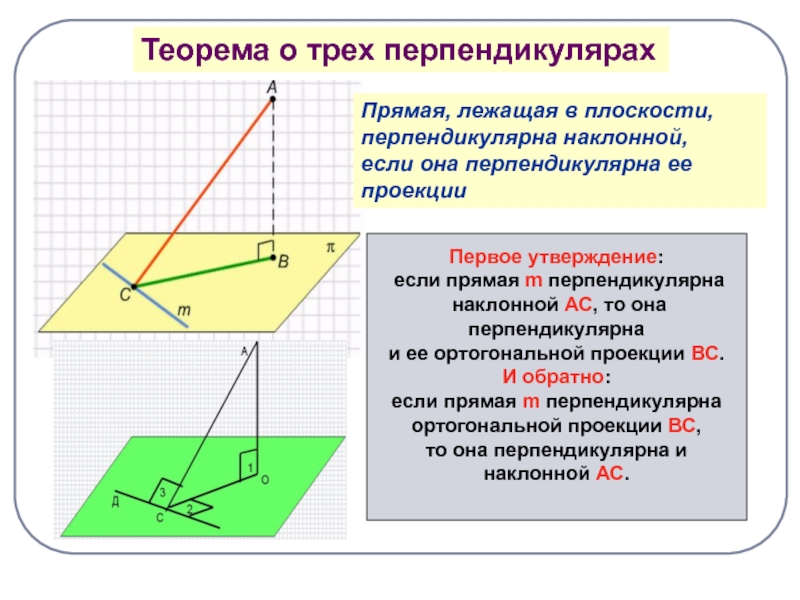
- 7. Теорема о трех перпендикулярахПрямая, лежащая в плоскости,
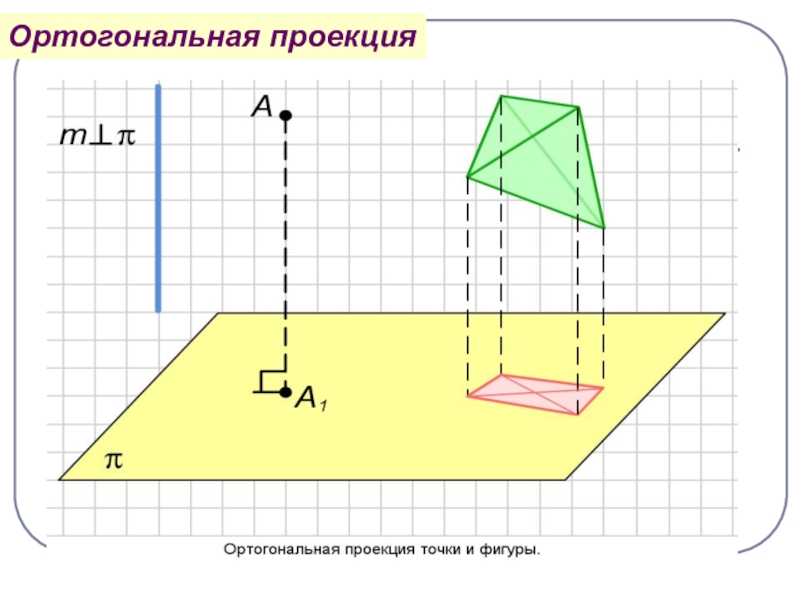
- 8. Ортогональная проекция
- 9. Слайд 9
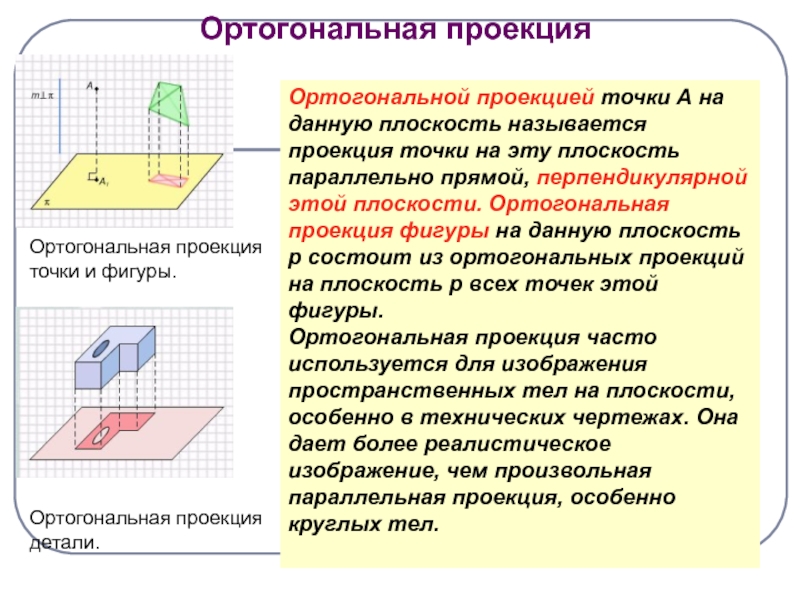
- 10. Ортогональной проекцией точки А на данную плоскость
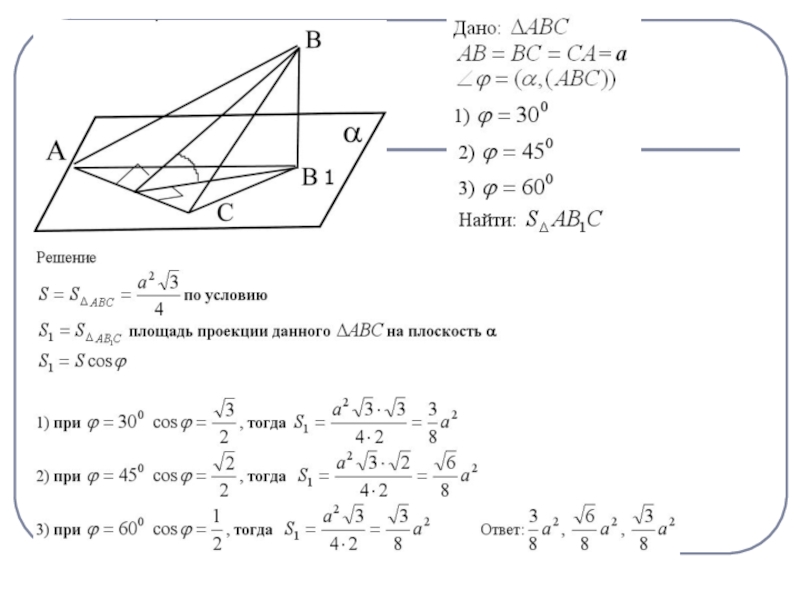
- 11. Площадь ортогональной проекции многоугольника на плоскость равна
- 12. Слайд 12
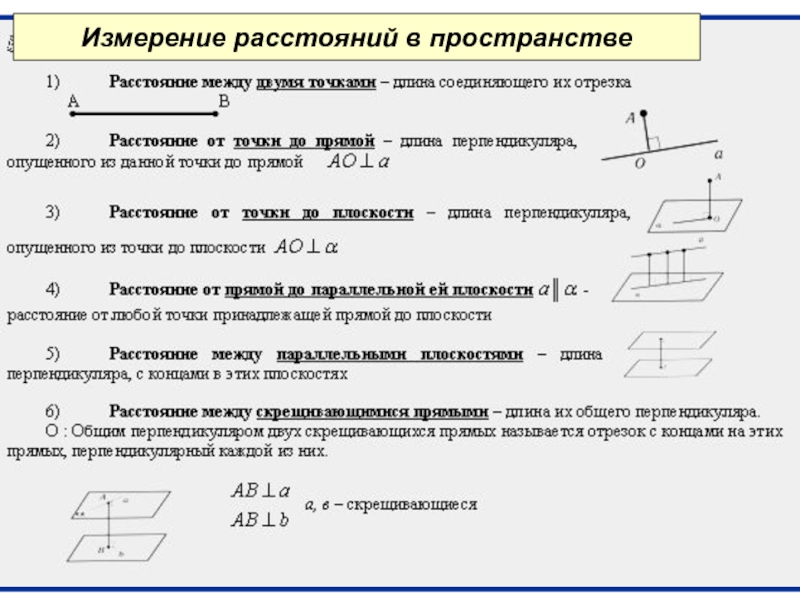
- 13. Измерение расстояний в пространстве
- 14. Измерение углов в пространстве Углом между прямой
- 15. Пусть и — данные плоскости,
- 16. Двугранным углом называется фигура, образованная прямой a
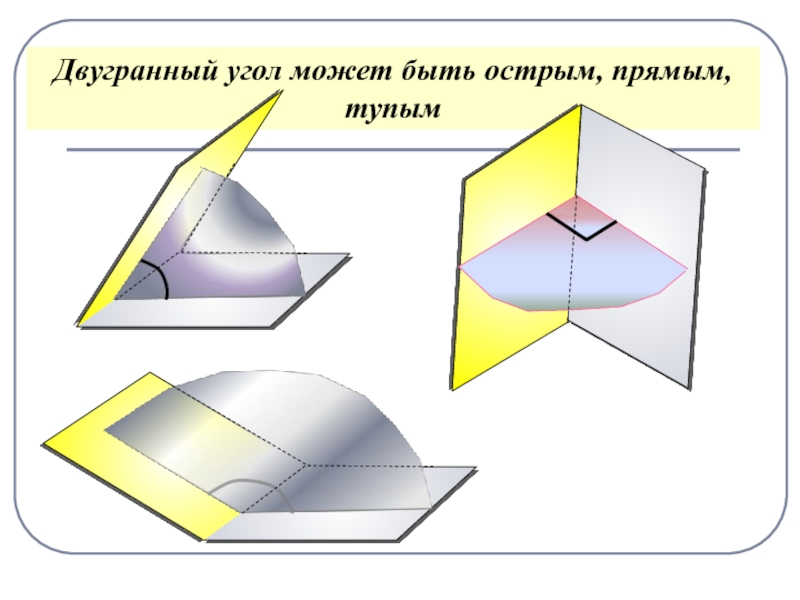
- 17. Двугранный угол может быть острым, прямым, тупым
- 18. Угол РDEK Двугранный угол АВNМ, ВN –
- 19. Угол РОК – линейный угол двугранного угла
- 20. Все линейные углы двугранного угла равны1Лучи ОА
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Перпендикулярность в пространстве
Определения и признаки
Перпендикуляр и наклонная, теорема
о трех перпендикулярах
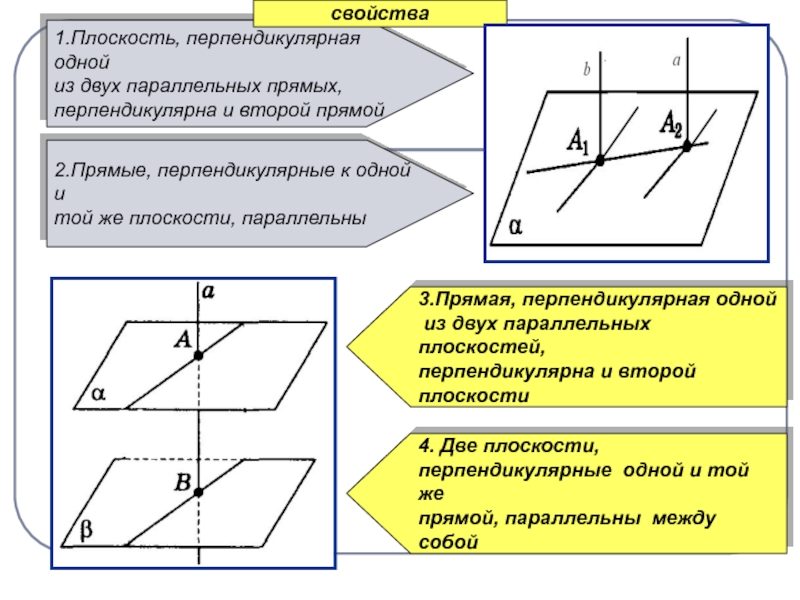
углов в пространствеСлайд 31.Плоскость, перпендикулярная одной
из двух параллельных прямых,
перпендикулярна и второй прямой
свойства
2.Прямые, перпендикулярные к одной и
той же плоскости, параллельны
3.Прямая, перпендикулярная одной
из двух параллельных плоскостей, перпендикулярна и второй
плоскости
4. Две плоскости,
перпендикулярные одной и той же
прямой, параллельны между собой
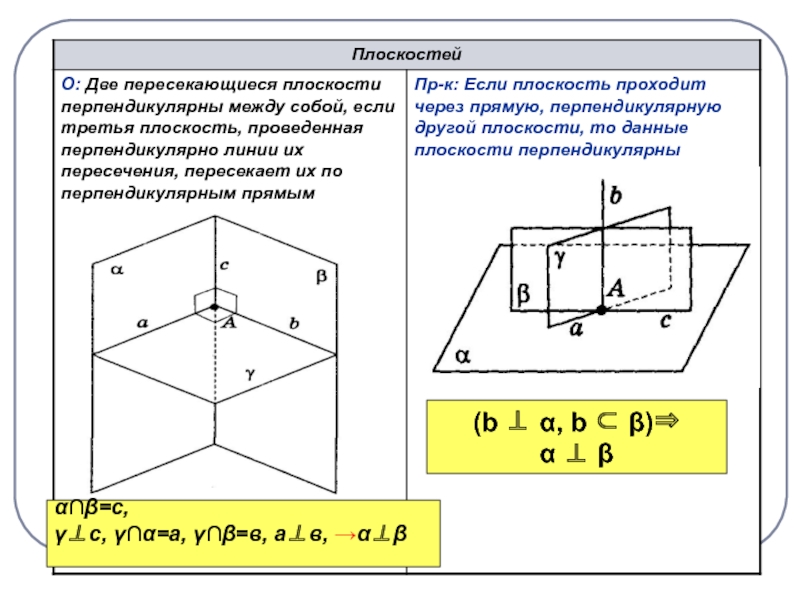
Слайд 5Если плоскости перпендикулярны,
то прямая лежащая в одной из них
перпендикулярно линии пересечения
плоскостей, будет перпендикулярна
и другой плоскости
=b, α
β, аα, ab, а β
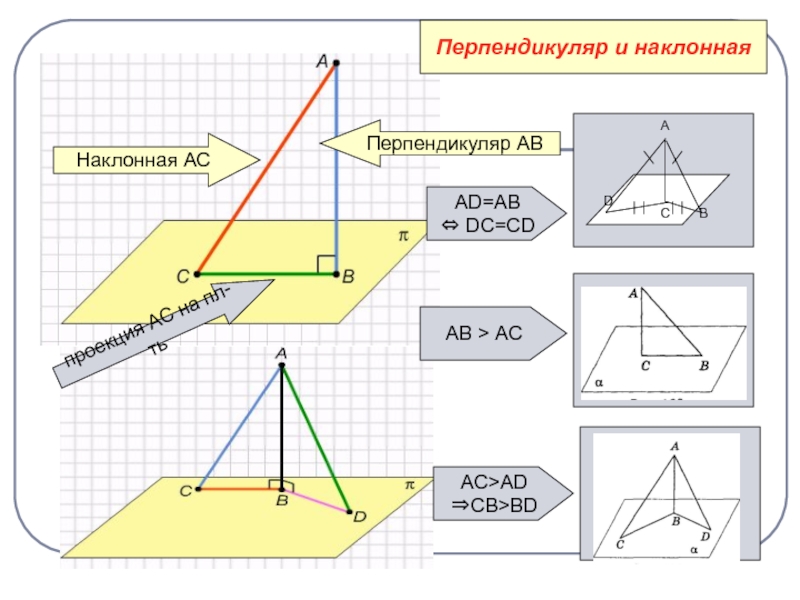
Слайд 6Перпендикуляр и наклонная
Перпендикуляр АВ
Наклонная АС
проекция АС на пл-ть
AD=AB
DC=CD
АВ > AC
AC>AD
CB>BD
Слайд 7Теорема о трех перпендикулярах
Прямая, лежащая в плоскости,
перпендикулярна наклонной,
если
она перпендикулярна ее
проекции
Первое утверждение:
если прямая m перпендикулярна
наклонной
АС, то она перпендикулярна
и ее ортогональной проекции ВС.
И обратно:
если прямая m перпендикулярна
ортогональной проекции ВС,
то она перпендикулярна и
наклонной АС.
Слайд 10Ортогональной проекцией точки А на данную плоскость называется проекция точки
на эту плоскость параллельно прямой, перпендикулярной этой плоскости. Ортогональная проекция
фигуры на данную плоскость p состоит из ортогональных проекций на плоскость p всех точек этой фигуры.Ортогональная проекция часто используется для изображения пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистическое изображение, чем произвольная параллельная проекция, особенно круглых тел.
Ортогональная проекция
Ортогональная проекция
точки и фигуры.
Ортогональная проекция
детали.
Слайд 11Площадь ортогональной проекции
многоугольника на плоскость
равна произведению его площади
на косинус угла между плоскостью
многоугольника и плоскостью проекции
Слайд 14Измерение углов в пространстве
Углом между прямой и плоскостью
называется угол между прямой и ее ортогональной проекцией на эту
плоскость.Если прямая параллельна плоскости, то угол между ней и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между ней и плоскостью прямой, т. е. равен 90°.
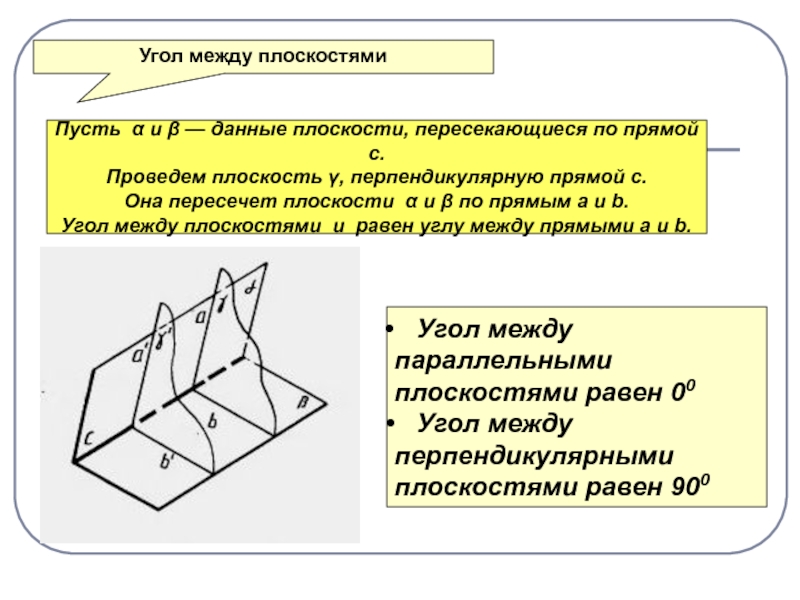
Слайд 15Пусть и — данные плоскости, пересекающиеся по прямой
с.
Проведем плоскость , перпендикулярную прямой с.
Она пересечет плоскости
и по прямым а и b. Угол между плоскостями и равен углу между прямыми а и b.
Угол между плоскостями
Угол между
параллельными
плоскостями равен 00
Угол между
перпендикулярными
плоскостями равен 900
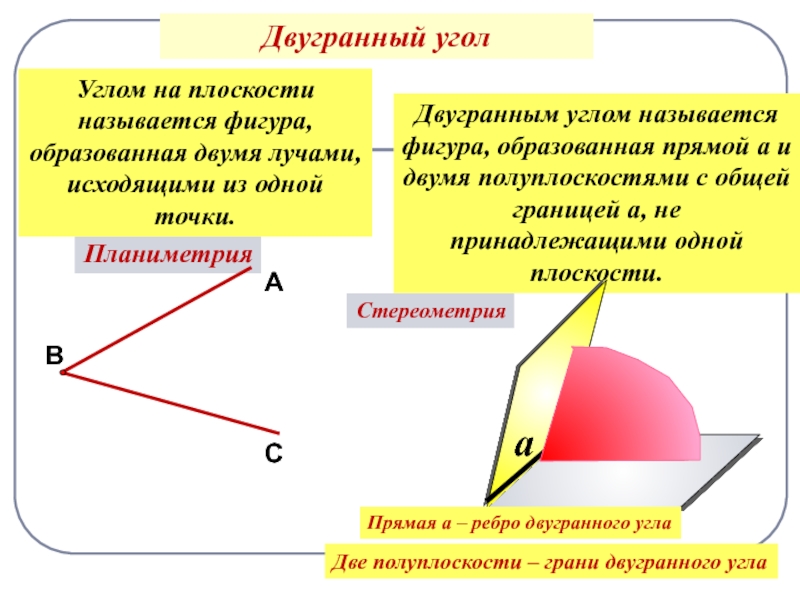
Слайд 16Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями
с общей границей a, не принадлежащими одной плоскости.
Планиметрия
Стереометрия
Углом на плоскости
называется фигура, образованная двумя лучами, исходящими из одной точки.Двугранный угол
а
Прямая a – ребро двугранного угла
Две полуплоскости – грани двугранного угла
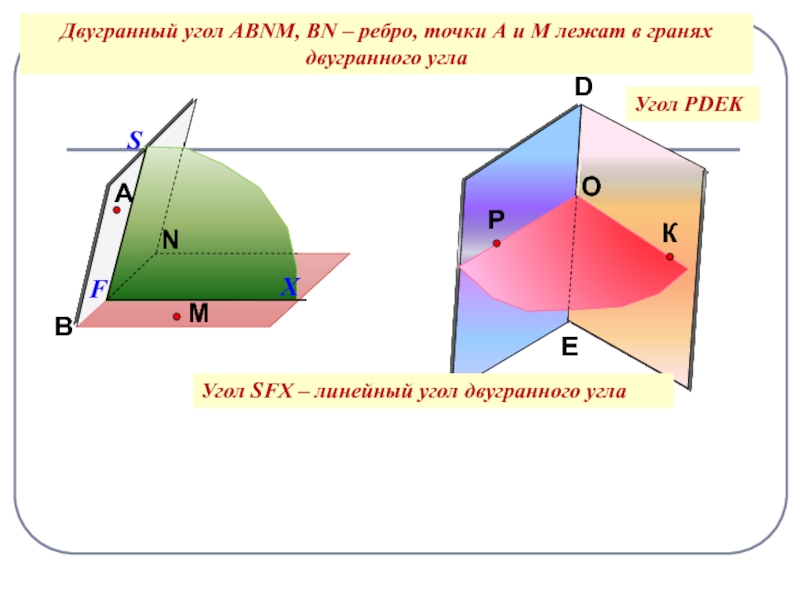
Слайд 18Угол РDEK
Двугранный угол АВNМ, ВN – ребро, точки А
и М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX – линейный
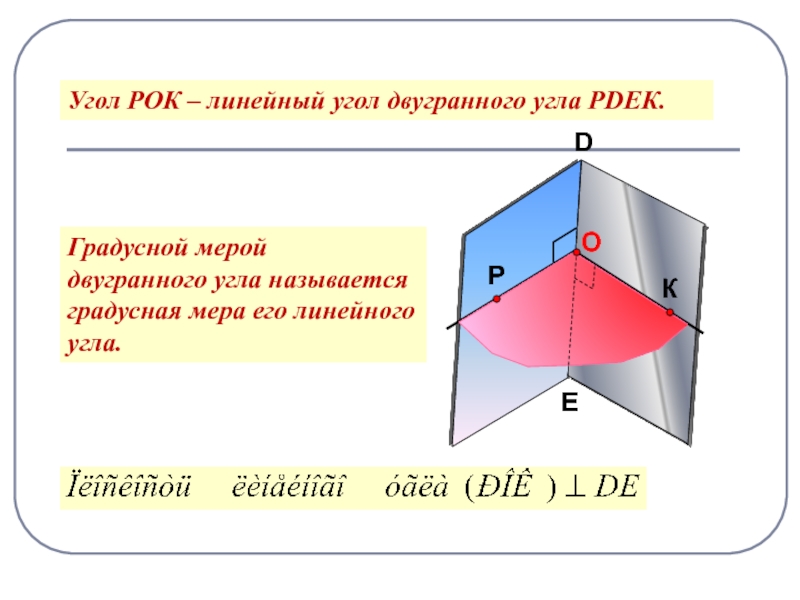
угол двугранного углаСлайд 19Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного
угла называется градусная мера его линейного угла.
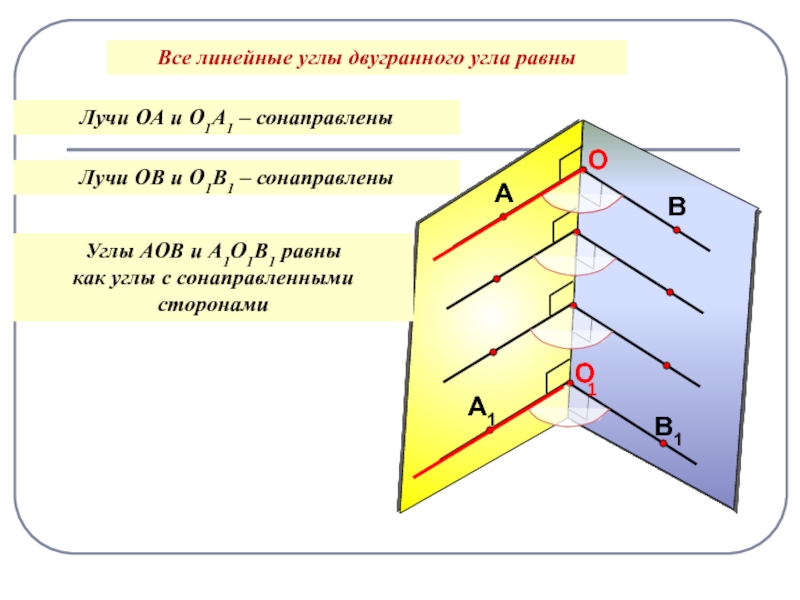
Слайд 20Все линейные углы двугранного угла равны
1
Лучи ОА и О1А1 –
сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и
А1О1В1 равныкак углы с сонаправленными сторонами