Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Первичное описание исходных данных
Содержание
- 1. Первичное описание исходных данных
- 2. Первичное описание исходных данныхРезультаты измерения для дальнейшего
- 3. Таблица данныхТаблица 1Х3i- самооценка до тренинга,Х4i- самооценка
- 4. Таблица частотЧастотой события называется количество случаев появления
- 5. Таблица частотПример: Необходимо распределить ответы всех учеников
- 6. Таблица частотгде fa — абсолютная частота некоторого
- 7. Таблица сгруппированных частотВо многих случаях признак может
- 8. Таблица 3Таблица частот, сгруппированных по интервалам времени решения тестовой задачи
- 9. Таблица – Результаты исследования интроверсииВариационный ряд -
- 10. Основные формулы для таблиц сгруппированных частот1. Число
- 11. Таблицы сопряженности, или кросстабуляцииТаблицы сопряженности, или кросстабуляции
- 12. Графики - это чертежи, которые можно использовать
- 13. В зависимости от круга решаемых задач выделяют
- 14. Секторная диаграмма – диаграмма, в которой числа
- 15. Графики (гистограмма распределения частот)Для более наглядного представления
- 16. Графики (гистограмма накопленных частот )Гистограмма накопленных частот
- 17. Полигон распределения частот Построение полигона распределения частот
- 18. Сглаженная кривая распределения частотВместо гистограммы или полигона
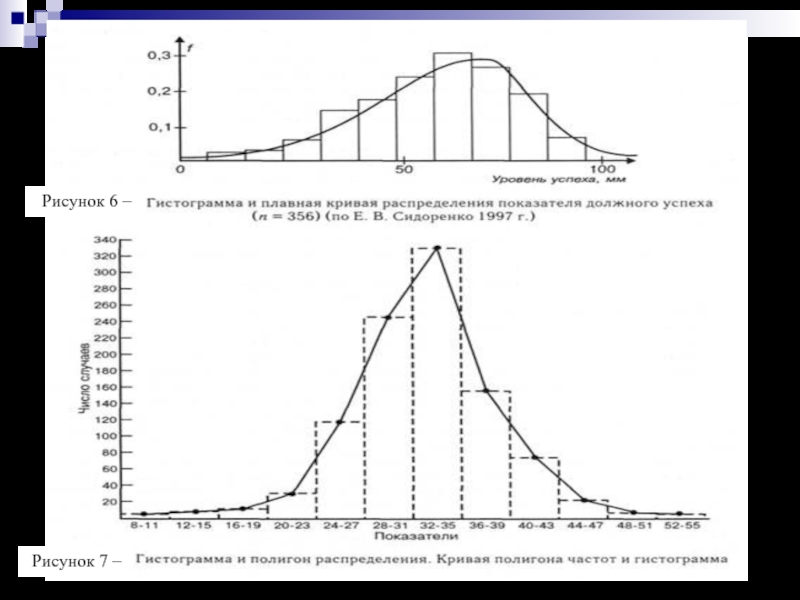
- 19. Рисунок 6 – Рисунок 7 –
- 20. Диаграмма размаха (ящечковая диаграмма) – диаграмма, которая
- 21. Графики следует использовать, когда надо отобразить общий
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Первичное описание исходных данных
Для первичного описания исходных данных используются таблицы
и графики.
одного - двух, а у множества объектов (испытуемых). Кроме того, каждый объект характеризуется не одним, а целым рядом признаков, измеренных в разных шкалах.Слайд 2Первичное описание исходных данных
Результаты измерения для дальнейшего анализа чаще всего
представляют в виде таблицы исходных данных. Каждая строка такой таблицы
обычно соответствует одному объекту, а каждый столбец - одному измеренному признаку. Таким образом, исходной формой представления данных является таблица типа «объект - признак».Слайд 3Таблица данных
Таблица 1
Х3i- самооценка до тренинга,
Х4i- самооценка после тренинга,
где I
- текущий номер испытуемого (меняется от 1 до N=60).
Слайд 4Таблица частот
Частотой события называется количество случаев появления событий.
Для изучения частоты
встречаемости значений интересующего признака (переменной) в имеющемся множестве наблюдений строятся
таблицы и графики распределения частот.Если указывается, сколько раз встречается каждое значение признака, то это - таблица абсолютных частот распределения, если указывается доля наблюдений, приходящихся на то или иное значение признака, то говорят об относительных частотах распределения (частность).
Еще одной разновидностью таблиц распределения являются таблицы распределения накопленных частот. Они показывают, как накапливаются частоты по мере возрастания значений признака.
Слайд 5Таблица частот
Пример: Необходимо распределить ответы всех учеников до проведения тренинга.
Для этого подсчитывают частоту встречаемости каждого из ответов и составляют
таблицу распределения частот (табл. 2).Таблица показывает, что чаще встречаются средние значения выраженности признака и реже - крайние значения.
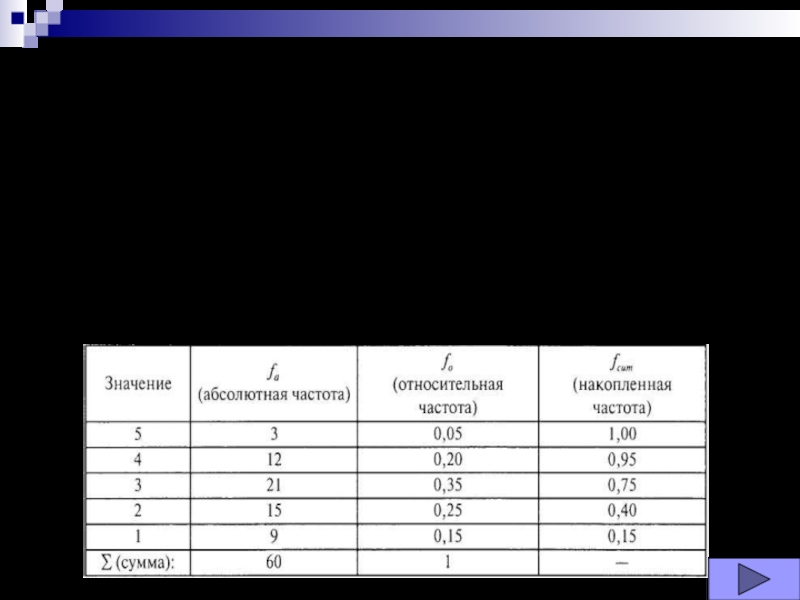
Таблица 2
Таблица распределения частот
Слайд 6Таблица частот
где fa — абсолютная частота некоторого значения признака, N-
число наблюдений, fо — относительная частота этого значения признака (частность).
Очевидно, что сумма всех абсолютных частот равна числу наблюдений - N, а сумма всех относительных частот равна 1. Нередко относительная частота применяется для оценки вероятности встречаемости значения.
Слайд 7Таблица сгруппированных частот
Во многих случаях признак может принимать множество различных
значений, например, если мы измеряем время решения тестовой задачи.
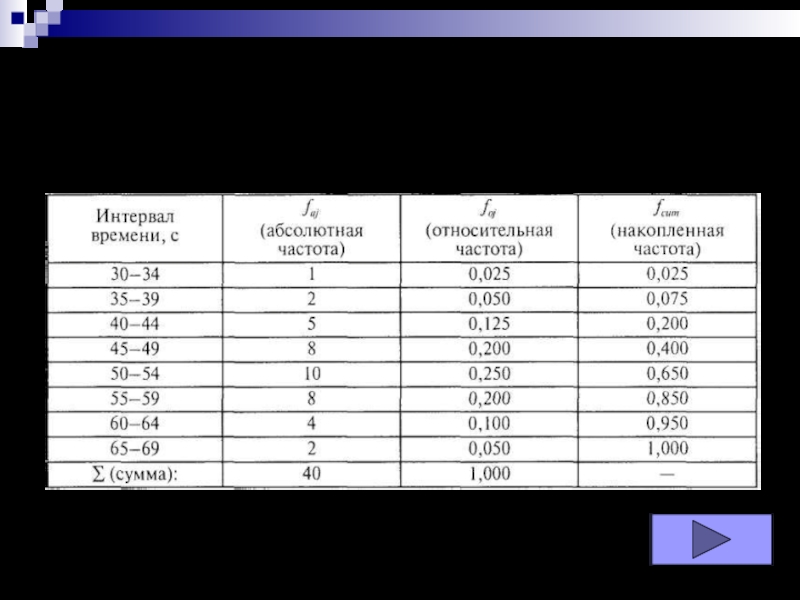
В
этом случае о распределении признака позволяет судить таблица сгруппированных частот, в которых частоты группируются по разрядам или интервалам значений признака.Слайд 9
Таблица – Результаты исследования интроверсии
Вариационный ряд - упорядоченное отражение распределения
значений признака, представляющий двойной ряд чисел и состоящий из обозначения
классов и соответствующих частот (частота встречаемости обозначается символом f).Числовой ряд является непрерывным.
Слайд 10Основные формулы для таблиц сгруппированных частот
1. Число разрядов (количество интервалов)-
от 6 до 15: k=
2. Объем разряда (интервал разряда):
Vраз ≥ (R+1)/k, где R- размах, к – количество разрядов.3. Количество «лишних вариантов (заступов)» =
= Vраз. округ* k – R – 1.
Задание: в группе испытуемых численностью 42 человек измерено время решения тестовой задачи. Были получены следующие значения: {63,35,58,53,45,61,37,58,51,40,60,55,43,57,50,61,44,64,45,77,53,46,47,72,49,51,64,52,56,58,59,60,49,64,32,51,64,65,69,66,40,69}.
Постройте таблицу сгруппированных частот.
Слайд 11Таблицы сопряженности, или кросстабуляции
Таблицы сопряженности, или кросстабуляции - это таблицы
совместного распределения частот двух и более номинативных признаков, измеренных на
одной группе объектов. Эти таблицы позволяют сопоставить два или более распределения. Столбцы такой таблицы соответствуют категориям (градациям) одного номинативного признака, а строки — категориям (градациям) другого номинативного признака.ЗАДАНИЕ: Построить таблицу сопряженности признаков «Пол» (две градации) и «Самооценка» (пять градаций) по таблице 1.
Слайд 12
Графики - это чертежи, которые можно использовать для наглядности распределения
количественно выраженной величины в выборке.
Диаграммы используются главным образом для
изображения соотношений между величинами. Это способ графического изображения величин при помощи фигур (секторов, столбцов и т.п.), площади которых пропорциональны этим величинам..
Слайд 13
В зависимости от круга решаемых задач выделяют диаграммы сравнения, структурные
диаграммы, диаграммы динамики.
Особым видом графиков являются диаграммы распределения величин, представленных
вариационным рядом. Это гистограмма, полигон и др.Слайд 14Секторная диаграмма – диаграмма, в которой числа (обычно проценты) изображены
в виде круговых секторов, имеющих такие площади.
Рисунок 1- Секторная диаграмма
Примечание:
Слайд 15Графики (гистограмма распределения частот)
Для более наглядного представления строится график распределения
частот или график накопленных частот.
Гистограмма распределения частот - это столбчатая
диаграмма, каждый столбец которой опирается на конкретное значение признака или разрядный интервал (для сгруппированных частот). Высота столбика пропорциональна частоте встречаемости соответствующего значения. Рис. 2. Гистограмма распределения частот самооценки (по данным таблицы 2)
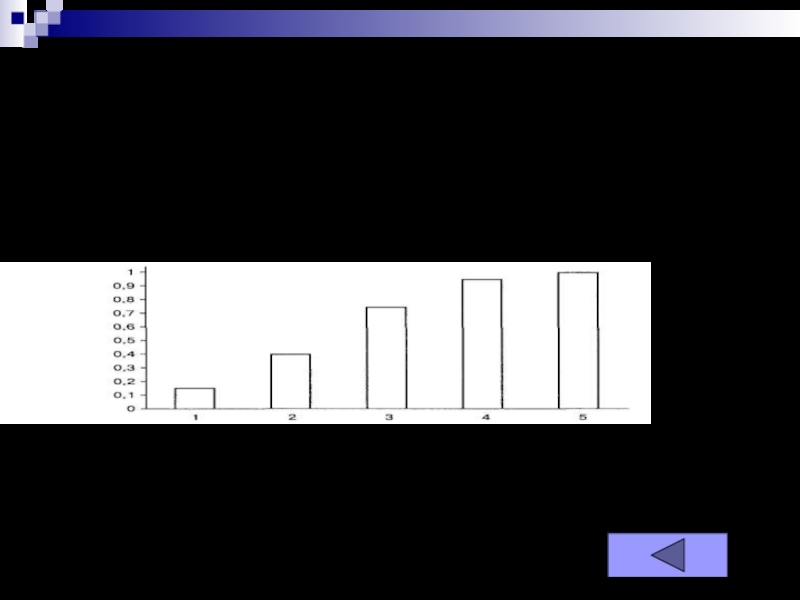
Слайд 16Графики (гистограмма накопленных частот )
Гистограмма накопленных частот отличается от гистограммы
распределения тем, что высота каждого столбика пропорциональна частоте, накопленной к
данному значению (интервалу). На рис. 3 изображена гистограмма накопленных частот для данных табл. 2.Рис. 3. Гистограмма накопленных относительных частот самооценки
Слайд 17Полигон распределения частот
Построение полигона распределения частот напоминает построение гистограммы.
В гистограмме вершина каждого столбца, соответствующая частоте встречаемости данного значения
(интервала) признака, - отрезок прямой.А для полигона отмечается точка, соответствующая середине этого отрезка. Далее все точки соединяются ломаной линией (рис. 4).
Рис. 4. Полигон распределения частот самооценки (по данным таблицы 2)
Слайд 18Сглаженная кривая распределения частот
Вместо гистограммы или полигона часто изображают сглаженную
кривую распределения частот. На рис. 5 изображена гистограмма распределения для
примера из табл. 3 (столбики) и сглаженная кривая того же распределения частот.Слайд 20Диаграмма размаха (ящечковая диаграмма) – диаграмма, которая Для каждой группы
вычисляется статистика центра (медиана или среднее) и статистики диапазона (например,
квартили или стандартные отклонения), и выбранные значения изображаются на диаграмме размаха. Также могут быть изображены точки выбросов (outliers).Рисунок 2 – Диаграмма размаха
Примечание:
Слайд 21
Графики следует использовать, когда надо отобразить общий характер функциональной зависимости.
Рекомендации по построению графиков:
должны включать все необходимые обозначения, чтобы быть
понятными сами по себе;2) график и текст должны взаимно дополнять друг друга;
3) на одном графике, как правило, не должно быть больше четырех кривых во избежание неразберихи;
4) надписи на осях графиков следует располагать внизу и слева;
5) линии на графике должны быть разной толщины в зависимости от их важности;
6) для обозначения точек наблюдения используются геометрические фигуры.