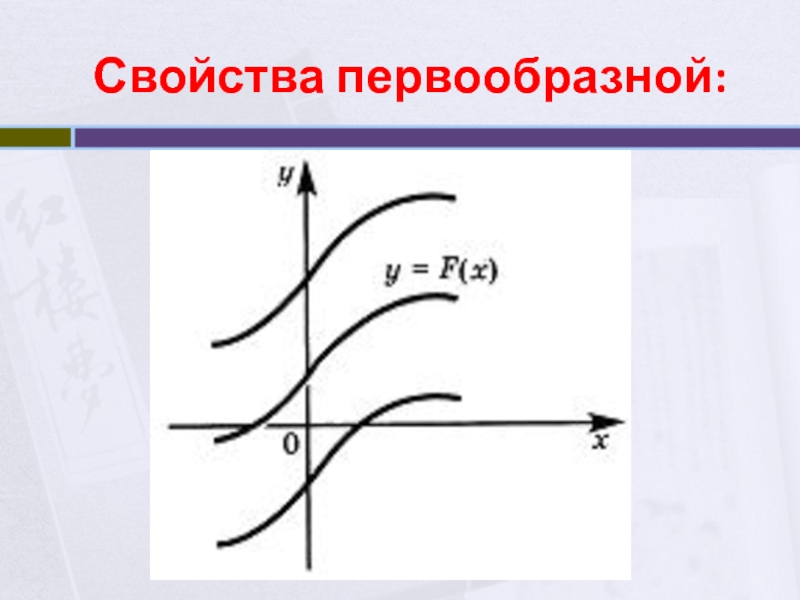
формулы интегрирования.
Непосредственное интегрирование (метод разложения).
Этапы интегрирования функций методом подстановки (замены
переменной).Интегрирование некоторых тригонометрических функций