Какие геометрические фигуры называются подобными?
Какие из фигур всегда
подобны, а какие нет?Какие треугольники подобны?
Похожие фигуры:
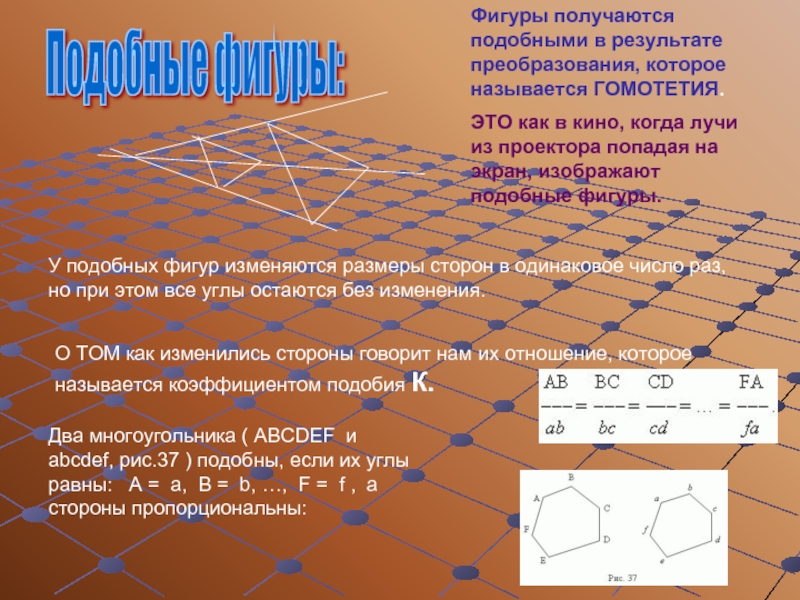
Подобные фигуры:
План исследования:
Полученные выводы!