Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
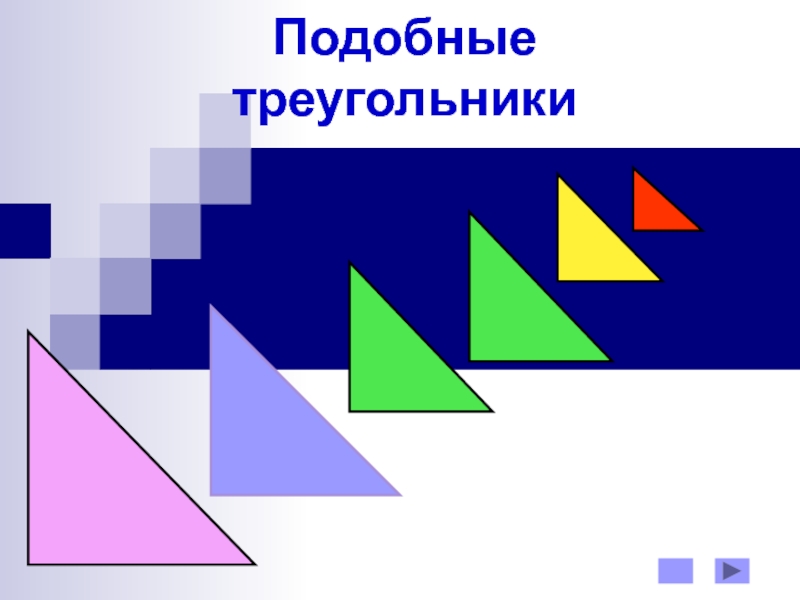
Подобные треугольники
Содержание
- 1. Подобные треугольники
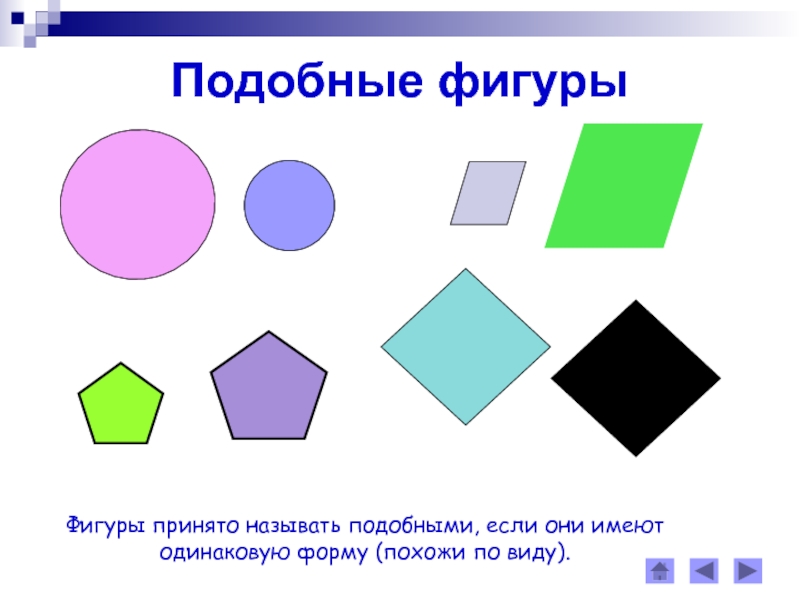
- 2. Подобные фигурыФигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).
- 3. Подобие в жизни(карты местности)
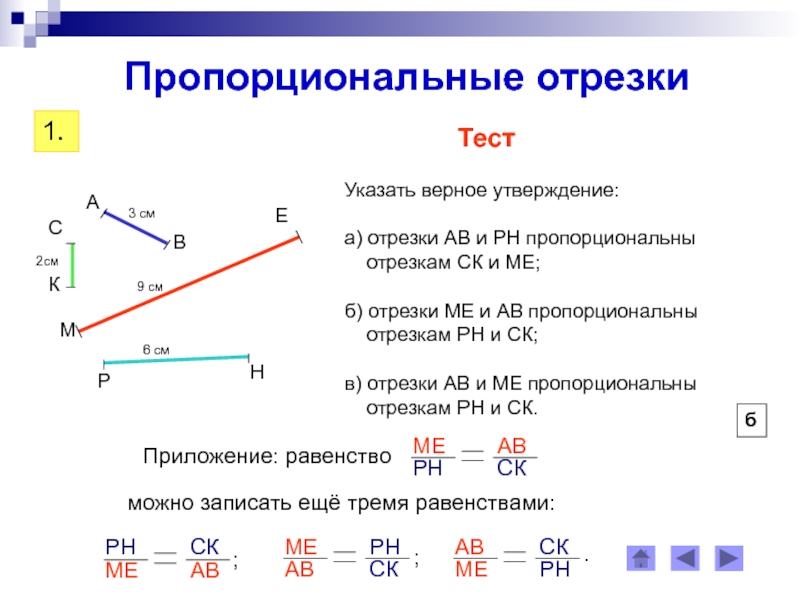
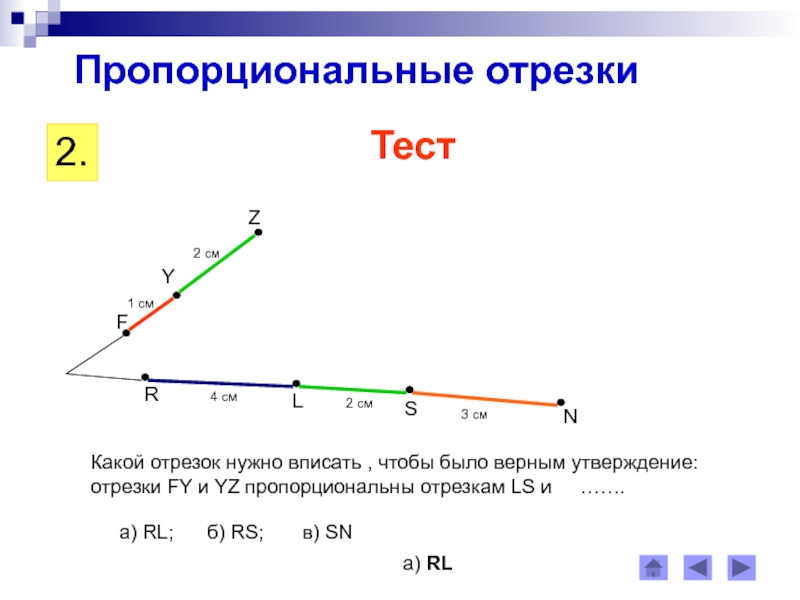
- 4. Пропорциональные отрезкиОпределение: отрезки называются пропорциональными,
- 5. бможно записать ещё тремя равенствами:
- 6. а) RL
- 7. Пропорциональные отрезки(нужное свойство)Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.Доказательство:
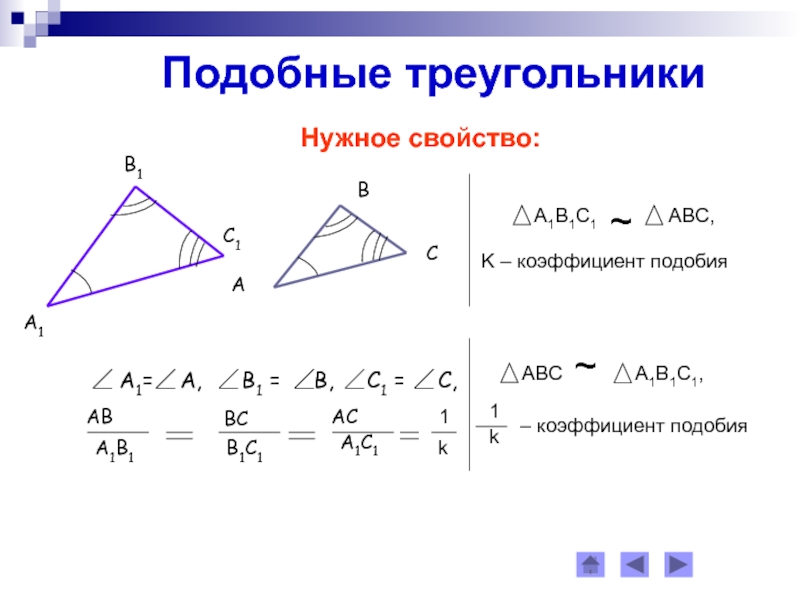
- 8. Подобные треугольникиОпределение: треугольники называются подобными, если углы
- 9. Подобные треугольникиНужное свойство:
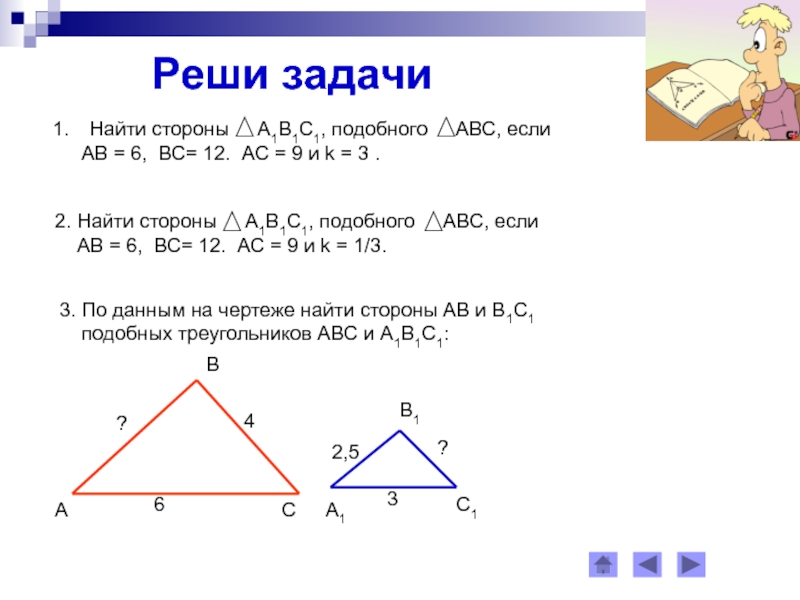
- 10. Реши задачи
- 11. Теорема 1. Отношение периметров подобных треугольников
- 12. Теорема 2. Отношение площадей подобных треугольников
- 13. « Математику уже затем учить следует, что
- 14. Скачать презентанцию
Подобные фигурыФигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).
Слайды и текст этой презентации
Слайд 2Подобные фигуры
Фигуры принято называть подобными, если они имеют
одинаковую форму
(похожи по виду).
Слайд 4Пропорциональные отрезки
Определение: отрезки называются пропорциональными,
если
пропорциональны их длины.Говорят, что отрезки А1В1 и С1К1 пропорциональны отрезкам АВ и СК.
Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если:
а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см ?
б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см ?
в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см ?
да
нет
нет
Слайд 7Пропорциональные отрезки
(нужное свойство)
Биссектриса треугольника делит противоположную сторону
на отрезки, пропорциональные
прилежащим
сторонам треугольника.
Доказательство:
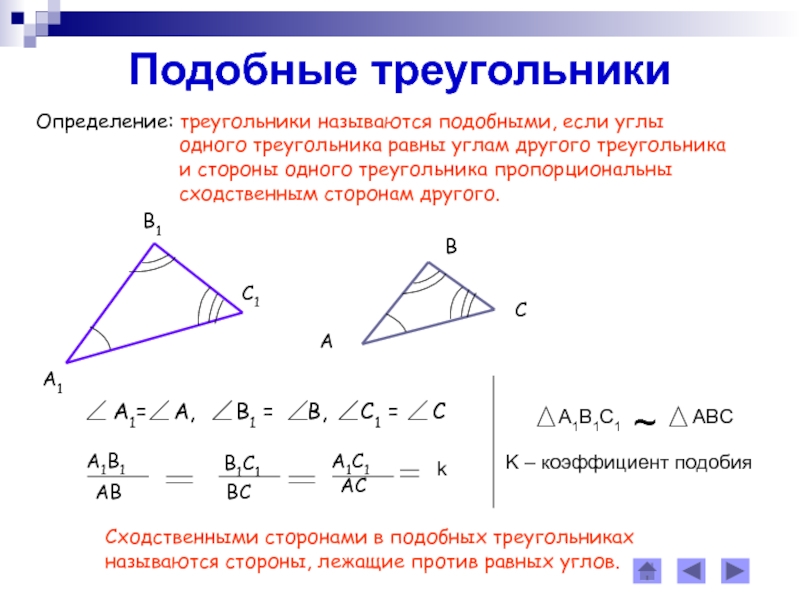
Слайд 8Подобные треугольники
Определение: треугольники называются подобными, если углы
одного треугольника
равны углам другого треугольникаи стороны одного треугольника пропорциональны
сходственным сторонам другого.
Сходственными сторонами в подобных треугольниках
называются стороны, лежащие против равных углов.
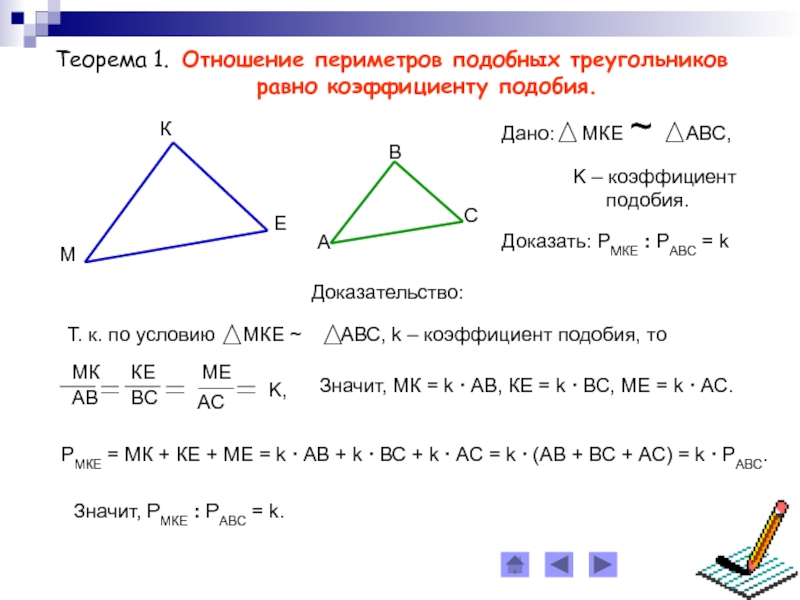
Слайд 11Теорема 1. Отношение периметров подобных треугольников
равно коэффициенту подобия.
Доказательство:
Значит,
МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС.РМКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ РАВС.
Значит, РМКЕ : РАВС = k.
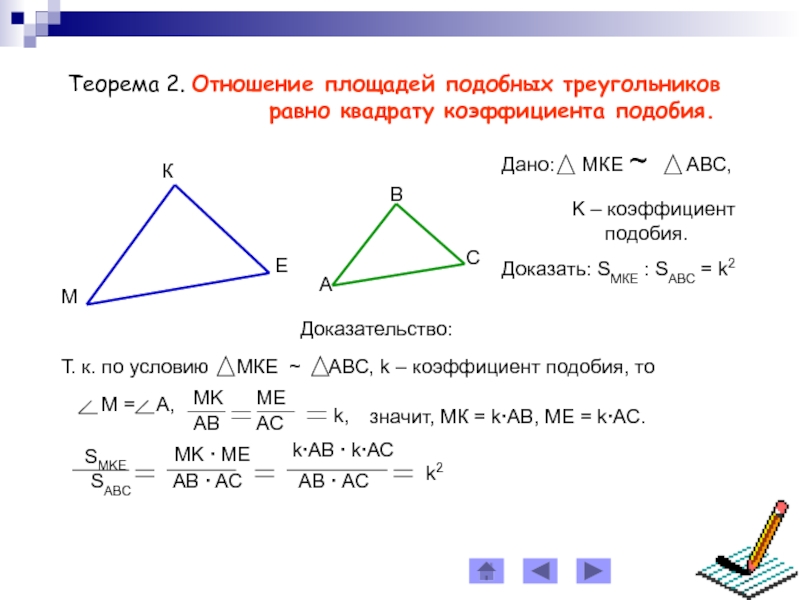
Слайд 12Теорема 2. Отношение площадей подобных треугольников
равно квадрату коэффициентa подобия.
Доказательство:
значит,
МК = k∙АВ, МЕ = k∙АС.
Слайд 13« Математику уже затем учить следует,
что она ум в
порядок приводит»
М. В. Ломоносов Желаю успехов в учёбе!
