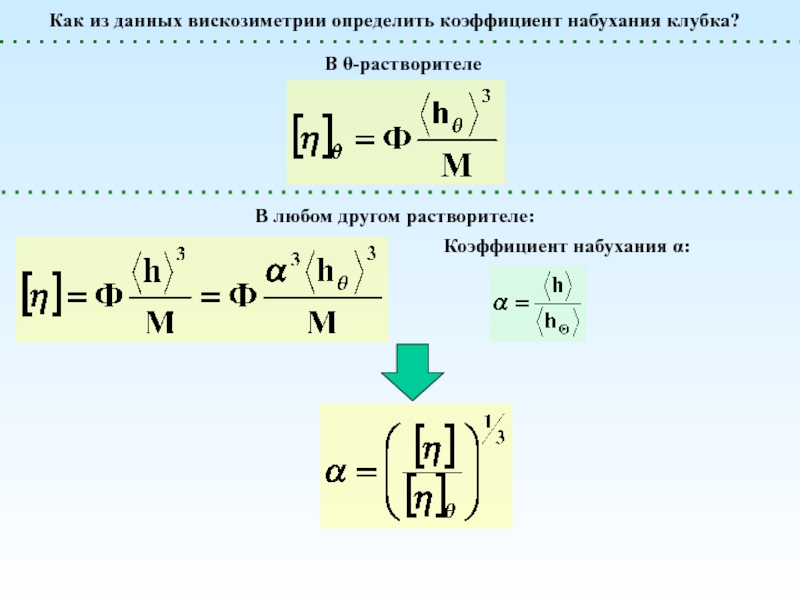
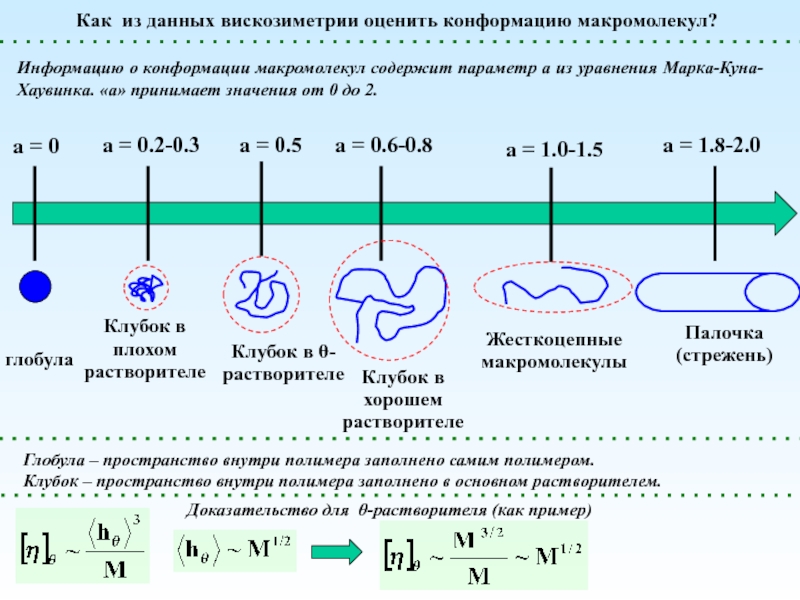
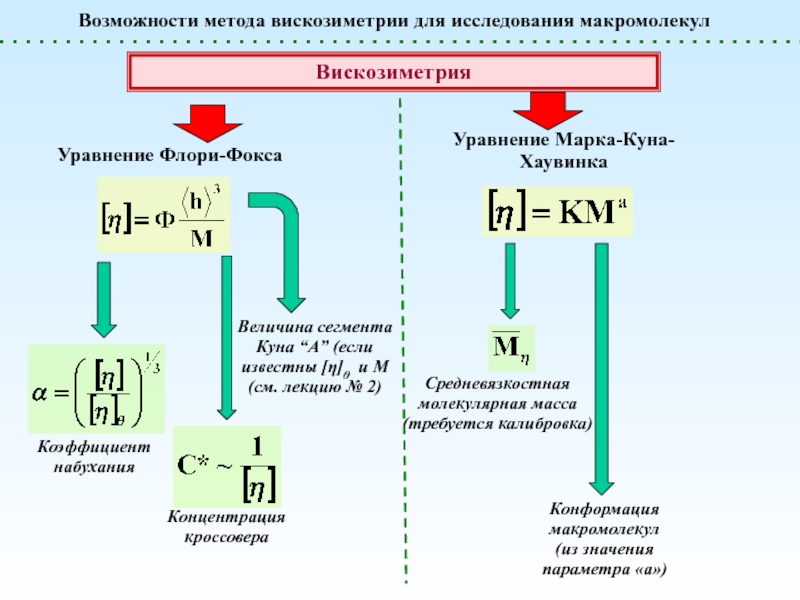
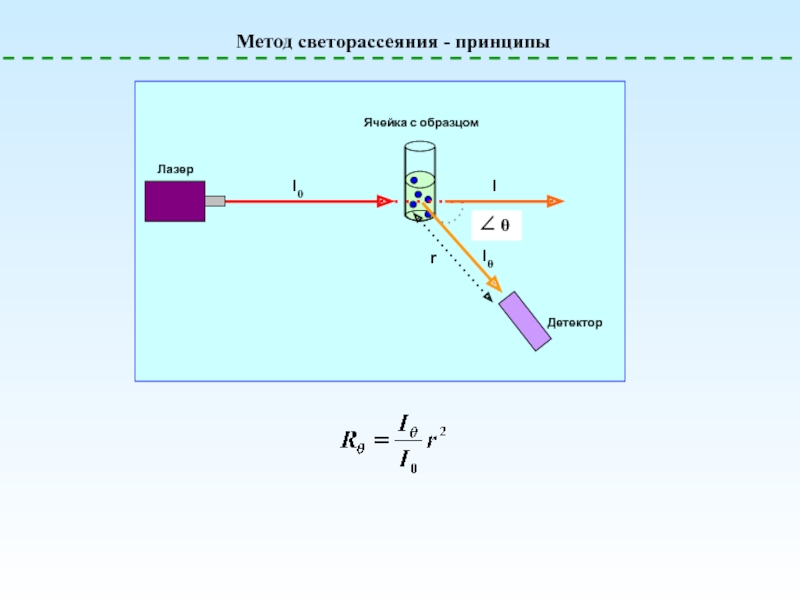
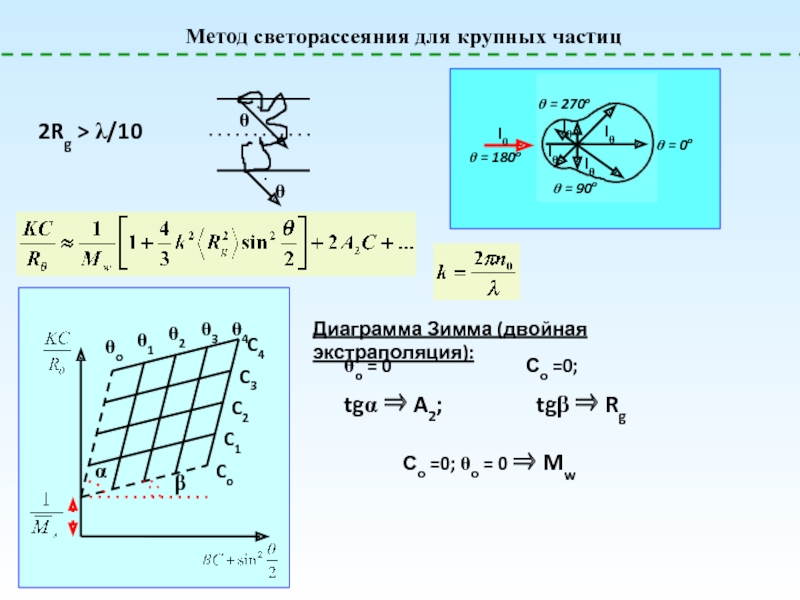
экспериментально? Каковы единицы их измерения?
Зачем нужны эти понятия?
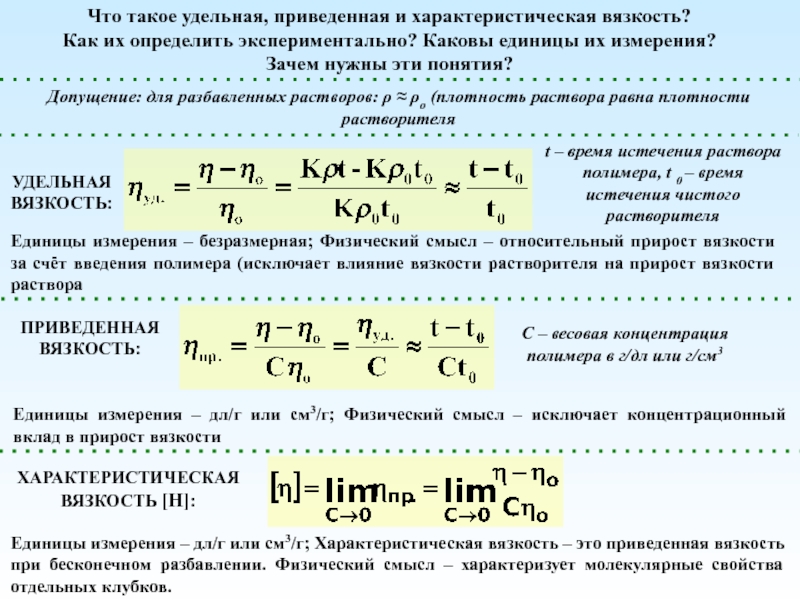
Удельная вязкость:
Допущение:
для разбавленных растворов: o (плотность раствора равна плотности растворителя
t – время истечения раствора полимера, t 0 – время истечения чистого растворителя
Единицы измерения – безразмерная; Физический смысл – относительный прирост вязкости за счёт введения полимера (исключает влияние вязкости растворителя на прирост вязкости раствора
приведенная вязкость:
С – весовая концентрация полимера в г/дл или г/см3
Единицы измерения – дл/г или см3/г; Физический смысл – исключает концентрационный вклад в прирост вязкости
Характеристическая вязкость []:
Единицы измерения – дл/г или см3/г; Характеристическая вязкость – это приведенная вязкость при бесконечном разбавлении. Физический смысл – характеризует молекулярные свойства отдельных клубков.
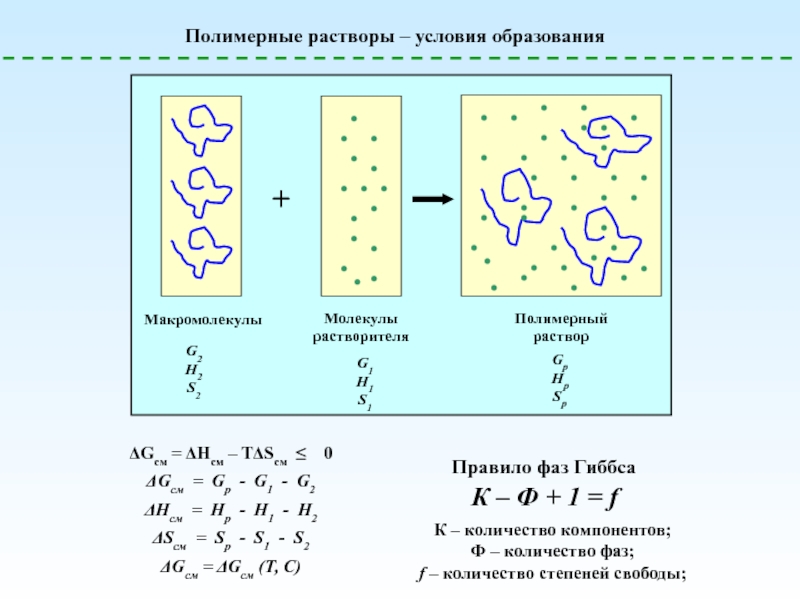
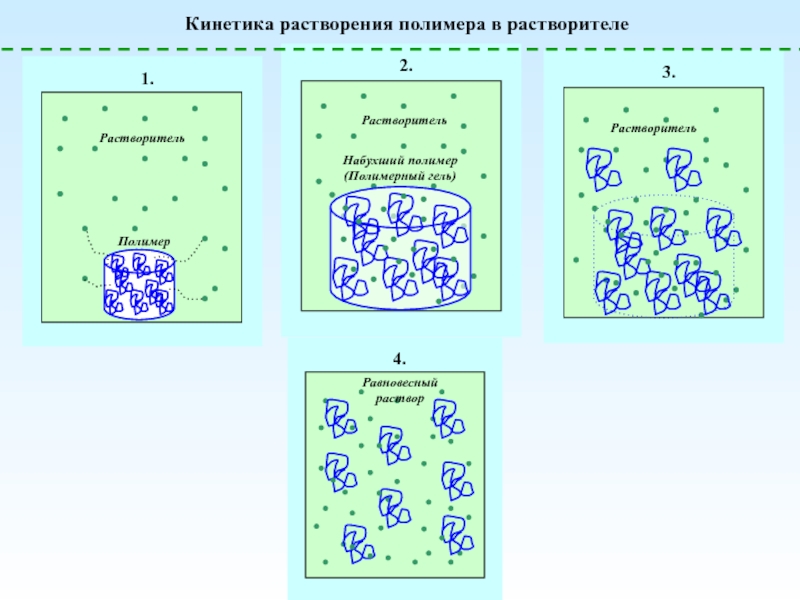
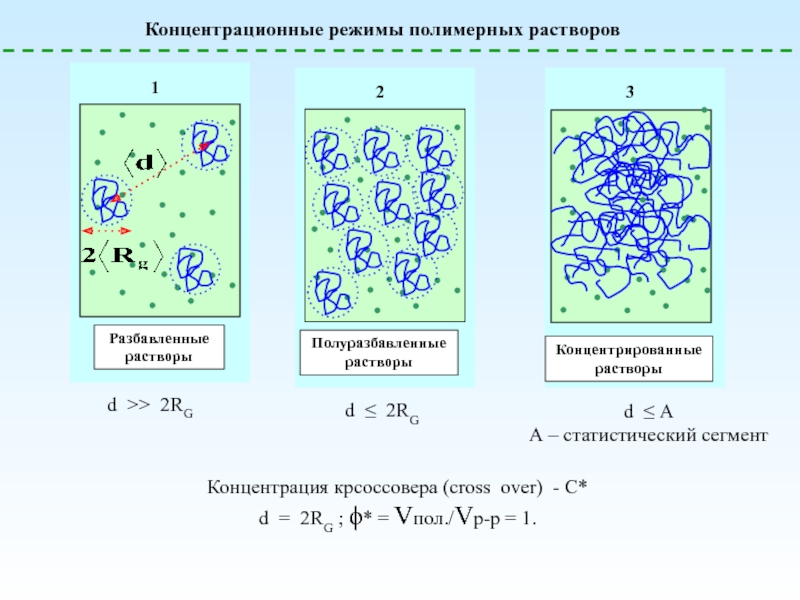
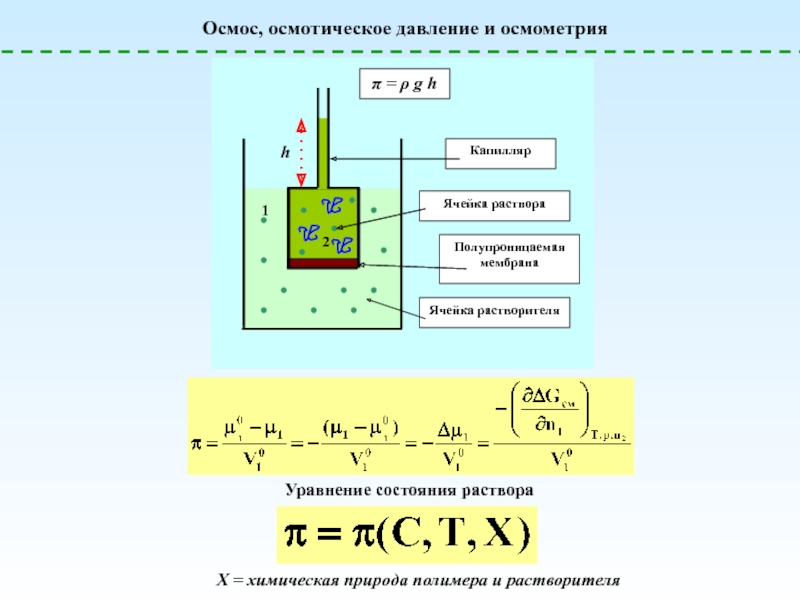
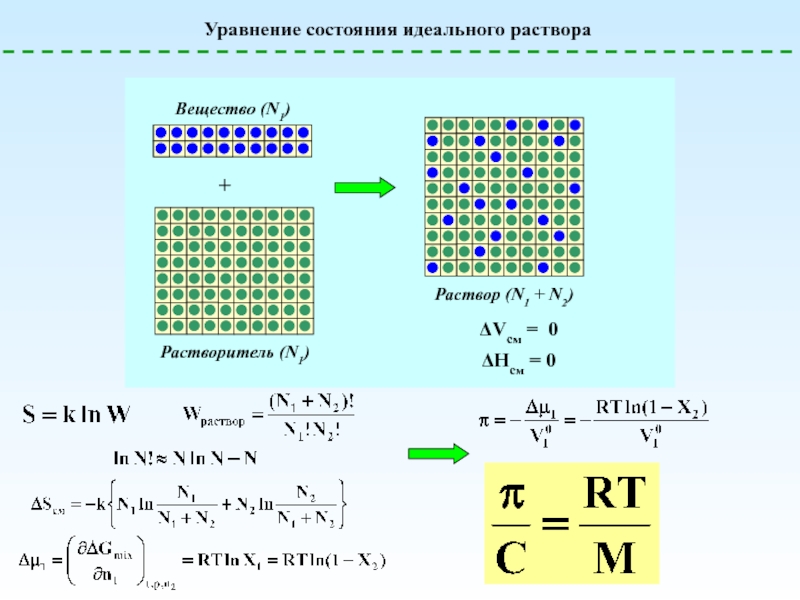
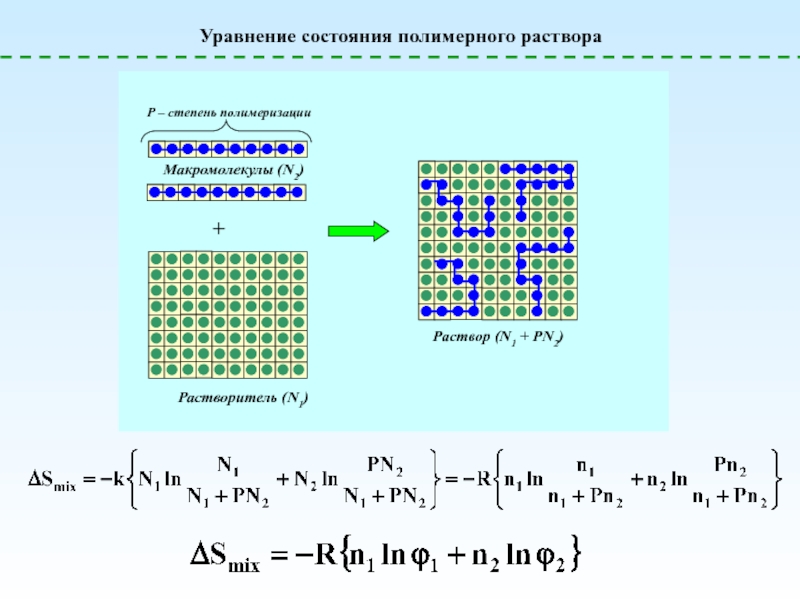
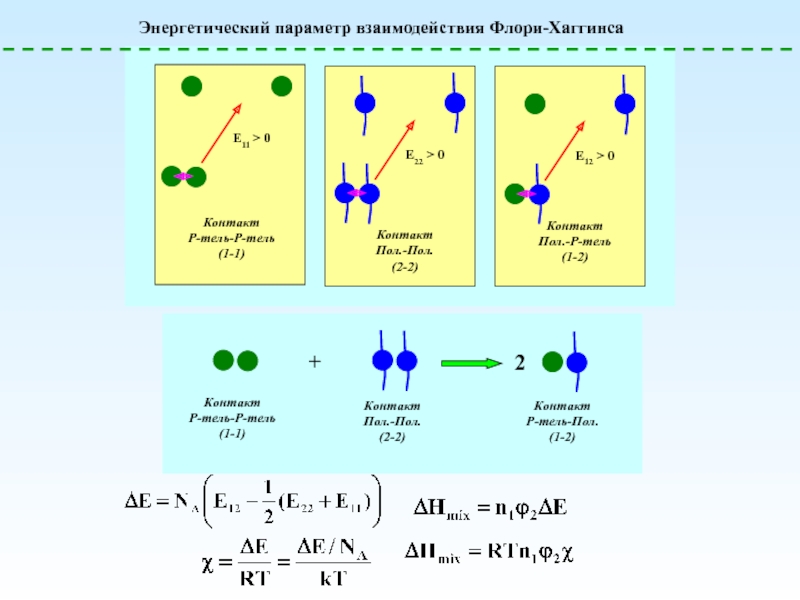




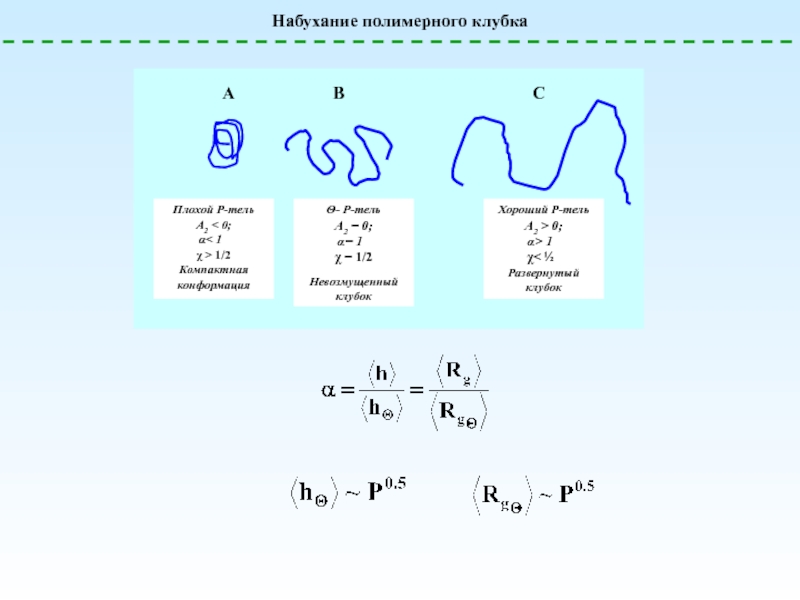
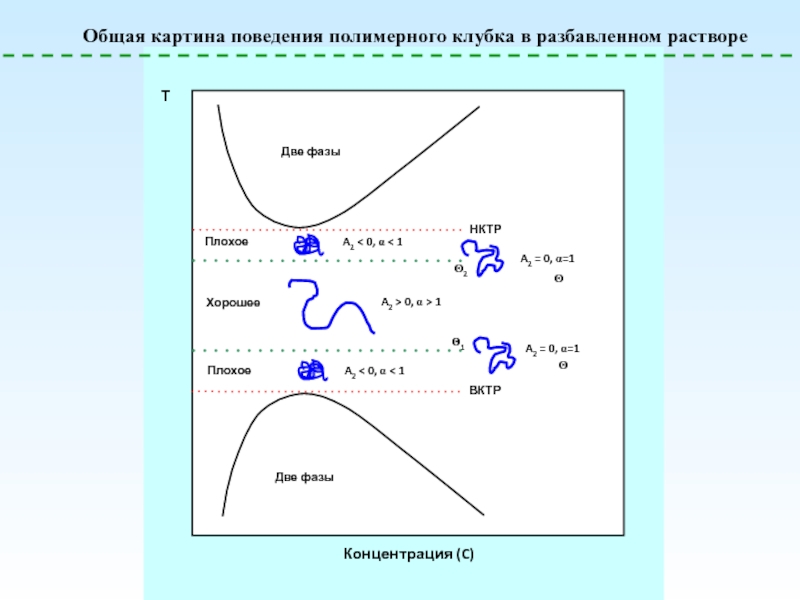



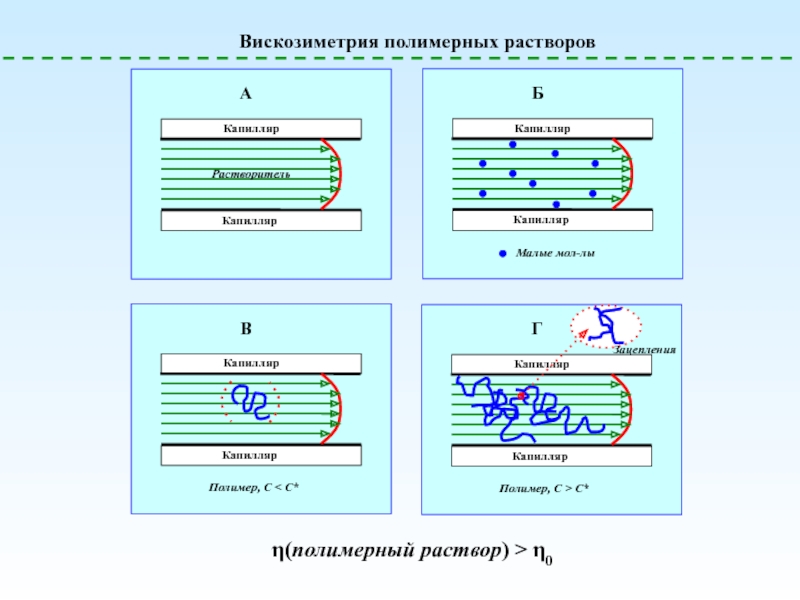
![Полимерные растворы – условия образования
Макромолекулы
G 2
H 2
S 2
+
Молекулы Вискозиметрия – определение вязкостиЗакон Ньютона = [пуаз] = [дин*сек/см2] = [г/(см*сек)]0.01 Вискозиметрия – определение вязкостиЗакон Ньютона = [пуаз] = [дин*сек/см2] = [г/(см*сек)]0.01 Пуаз = сПуазВязкость воды – 1](/img/thumbs/00cf81e378e4feb7204e1198aea19be4-800x.jpg)