Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Полуэмпирическая квантовая химия
Содержание
- 1. Полуэмпирическая квантовая химия
- 2. молекулярная динамика и метод Монте-Карло неэмпирическая квантовая
- 3. Полуэмпирическая квантовая химияИдея: 1) вместо точного оператора
- 4. 3) Для двухэлектронных интегралов вводят приближение Нулевого
- 5. 4) Результат расчета не должен зависеть от
- 6. Вращательная инвариантность нарушается каждый раз, когда двухэлектрон-ные
- 7. Приближение НДП для двухэлектронных интегралов Двухэлектронные интегралы
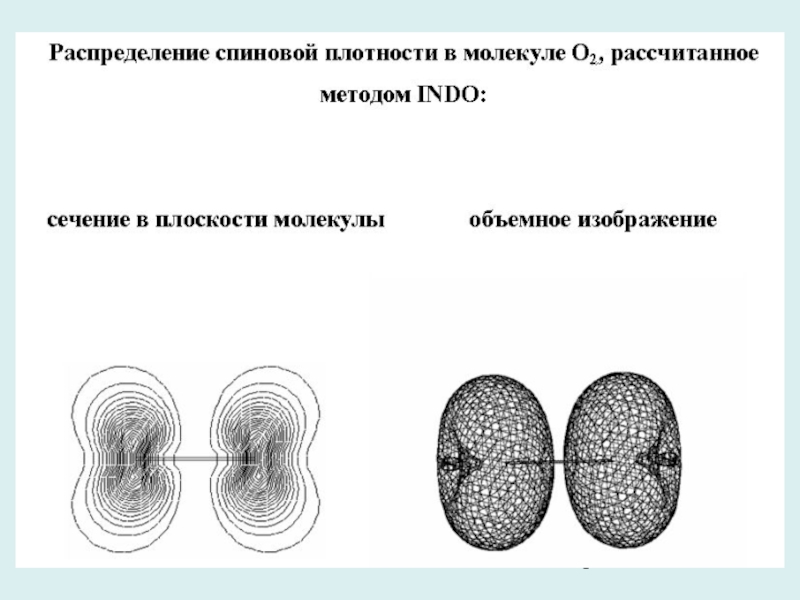
- 8. Слайд 8
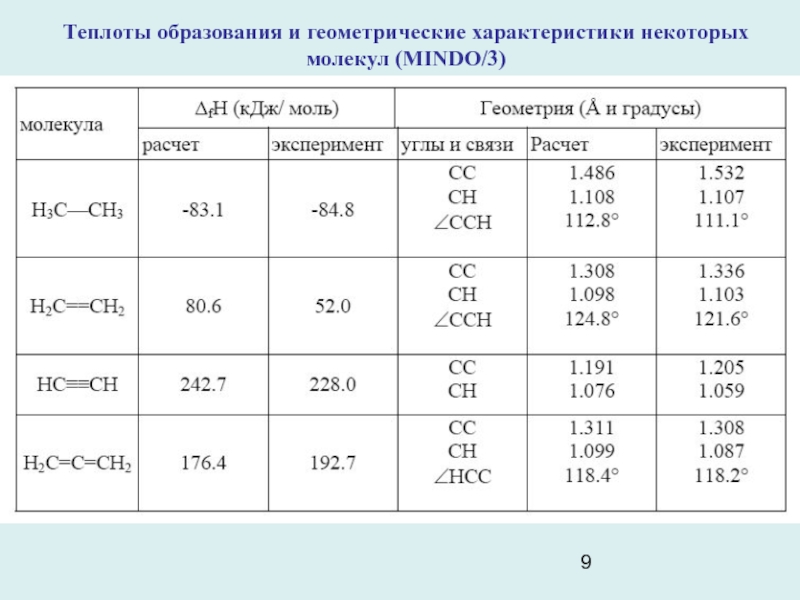
- 9. Теплоты образования и геометрические характеристики некоторых молекул (MINDO/3)
- 10. Длины связей (A), валентные углы (град.) молекул,
- 11. Метод Модифицированного Пренебрежения Дифференциальным Перекрыванием (MNDO)MNDO более
- 12. Разделение σ- и π-электронов. π-электроннное приближение
- 13. ψσ и ψπ - нормированные антисимметричные по
- 14. Обычно учитывают несколько однократно возбужденных электронных конфигураций
- 15. Диагонализизация матрицы hπ i→k, j→l
- 16. Метод МО ХюккеляЭто не-ССП метод,
- 17. Полная энергия в этом методе
- 18. х= -1 → с1 = с2 .
- 19. Вековое уравнение для таких систем выглядит следующим
- 20. Схема π–электронных уровней энергии в зависимости от
- 21. Энергетические уровни для циклической системы, включающей n
- 22. Расширенный метод Хюккеля (Хоффман, 1963)
- 23. NDO – нулевое дифференциальное перекрывание:
- 24. Слайд 24
- 25. Точность квантово-химических расчетов свойств молекула)Точность неэмпирического расчета
- 26. -энтропии ~ 0.5 энтропийной единицы (ккал/К моль);-присоединение/отщепление
- 27. Ошибка расчета энергии образования органических
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Компьютерное моделирование процессов нанотехнологий.
Российский химико-технологический университет им. Д.И. Менделеева
Кафедра
квантовой химии
Бобров М.Ф. «Квантовая химия молекул».Слайд 2молекулярная динамика
и метод Монте-Карло
неэмпирическая
квантовая химия
полуэмпирическая
квантовая
химия
квантовая
статистическая
механика
молекулярная
механика
Методы вычислительной химия наноразмерных систем
Слайд 3
Полуэмпирическая квантовая химия
Идея: 1) вместо точного оператора Фока - приближенный,
элементы которого получают из эмпирических данных; параметры одно- и двухэлектронных
интегралов подбирают для каждого атома или для пар атомов.2) многоэлектронная волновая функция – один детерминант, базисные функции ℵi – симметричные ортогональные комбинации ОСТ {χj }, которые получаются из исходных ОСТ с помощью преобразования Левдина ℵ= χS-1/2.
Расчет МО проводится обычным итерационным путем.
Важно: параметры справедливы лишь в пределах узкого класса соединений, поэтому придавать им физический смысл не следует.
Основные приближения полуэмпирических методов
1) Рассматриваются только валентные электроны: электроны атомных остовов включают в функции, описывающие энергию отталкивания остов-остов. Поляризацией остовов пренебрегают.
2) Базис считают минимальный, полагая, что базисные функции образуют набор ортогональных АО.
Слайд 43) Для двухэлектронных интегралов вводят приближение Нулевого Дифференциального Перекрывания (НДП)
χμ(
r )χν( r )dr =0. μ≠ν
Считают, что
из-за экспоненциального убывания АО двухэлектронными кулоновскими и обменными интегралами, содержащими произведения различных атомных орбиталей, зависящих от одного аргумента, можно пренебречь:(μν⎮λσ) = (μν⎮λσ)δμν δλσ = (μμ⎮λλ)
В приближении НДП, принимаемом для всех пар АО, уравнения Рутана имеют вид:
Элементы матрицы Фока:
Слайд 54) Результат расчета не должен зависеть от выбора декартовой системы
координат, в которой определяются ориентации p-, d- и т.д. АО.
НДП нарушает это требование. Например, двухцентровый кулоновский интеграл (px py⎪s2), где px и py - АО одного и того же атома в приближении НДП должен быть равен нулю. Повернем теперь декартову систему координат вокруг оси z на угол θ: тогда p′x = px cosθ + py sinθp′y = px sinθ - py cosθ и
(p′x p′y⎪s2) = - (p 2x ⎪s2) cosθ sinθ + (p 2y ⎪s2) cosθ sinθ +
(px py ⎪s2)( cos2θ - sin2θ)= [(p 2y ⎪s2) - (p 2x ⎪s2) ] cosθ sinθ
(s-АО при повороте не меняется, px и py АО ортогональны). (2.49) равно нулю только при θ=00 или 900 , т.е. интеграл (px py⎪s2) не инвариантен относительно поворота системы координат.
Иллюстрация происхождения неинвариантности двухцентрового кулоновского интеграла по отношению к повороту осей координат
Слайд 6Вращательная инвариантность нарушается каждый раз, когда двухэлектрон-ные интегралы включают перекрывание
двух АО одного и того же атома.
Поэтому в таких
случаях вводится еще одно приближение: считают, что двухэлектронные интегралы (μμ⎮λλ) зависят только от природы атомов, на которых центрированы орбитали χμ и χλ , и не зависят от конкретного вида орбиталей. Это соответствует сферическому усреднению распределения валентных электронов на АО различных атомов молекулы при расчете взаимодействия и обеспечивает инвариантность решения относительно поворота систем координат.
Для усредненного интеграла (μμ⎮λλ) используется обозначение γAB , где А и В обозначают атомы, на которых центрированы АО интегралы μ и λ; вычисляется он с s-АО соответствующих атомов
γAB = (s2A⎮ s2B)
Для одноэлектронных интегралов также вводятся различные приближения, которые рассмотрим далее применительно к конкретным методам.
Слайд 7Приближение НДП для двухэлектронных интегралов
Двухэлектронные интегралы в приближении НДП
принимают равными нулю, если они включают перекрывание пар АО разных
атомов или пары разных АО одного и того же атома. Однако для р-АО вращательная инвариантность нарушается в любом случае. Поэтому вводится еще одно приближение: считают, что двухэлектронные интегралы (μμ⎮λλ) зависят только от природы атомов, на которых центрированы орбитали χμ и χλ , и не зависят от конкретного вида орбиталей. Это соответствует сферическому усреднению распределения валентных электронов на АО различных атомов молекулы при расчете взаимодействия и обеспечивает инвариантность решения относительно поворота систем координат.Для усредненного интеграла (μμ⎮λλ) используется обозначение γAB , где А и В обозначают атомы, на которых центрированы АО интегралы μ и λ.
Интеграл γAB вычисляется с помощью s-АО соответствующих атомов
γAB = (s2A⎮ s2B)
или по специальным эмпирическим формулам.
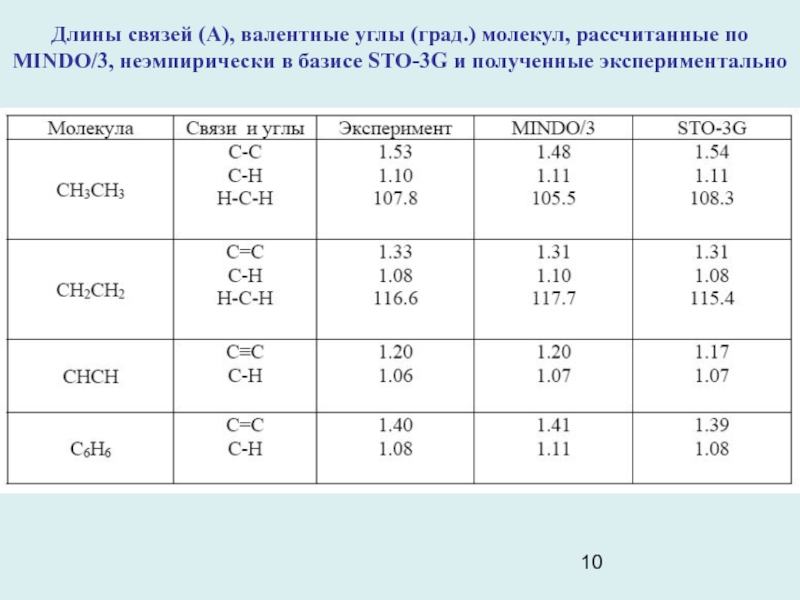
Слайд 10Длины связей (A), валентные углы (град.) молекул, рассчитанные по MINDO/3,
неэмпирически в базисе STO-3G и полученные экспериментально
Слайд 11Метод Модифицированного Пренебрежения Дифференциальным Перекрыванием (MNDO)
MNDO более корректно описывает отталкивание
неподеленных электронных пар за счет учета всех двухэлектронных интегралов, содержащих
пары АО одного и того же атома; перекрывание АО различных атомов игнорируется (приближение двухатомным дифференциальным перекрыванием). Параметры зависят только от свойств отдельных атомов, а не от их парных комбинаций → параметризация по большему числу соединенийСуществуют различные схемы, отличающиеся выбором параметров: AM1, AM3 (Austin Model), PM3 (Parameterised Model 3) и др. Они обеспечили возможность расчета водородной и энергии образования органических молекул и переходных состояний органических реакций с ошибкой менее 5 ккал/моль.
Слайд 12Разделение σ- и π-электронов. π-электроннное приближение
Для плоских молекул
все валентные АО можно разбить на две группы. Одна из
них содержит орбитали, симметричные относительно отражения в плоскости молекулы ( σ-АО ), другая - орбитали, антисимметричные относительно такого отражения (π-АО). σ-электроны имеют максимальную вероятность нахождения в плоскости молекулы; π-электроны слабее связаны с остовом молекулы, более подвижны, легче ионизируются и более активны во взаимодействиях.Свойства ненасыщенных и ароматических систем – высокая реакционная способность, зависимость от заместителей, спектры и т.д – определяются, в основном, именно электронами, описываемыми π-орбиталями. Поэтому при решении уравнений Рутана для таких систем вводят π-электронное приближение: σ-АО считают неполяризованными и включают в атомный остов, а движение π-электронов рассматривают в потенциальном поле таких остовов.
Волновая функция молекулы представляется как произведение
ψ = ψσ ψπ.
Слайд 13ψσ и ψπ - нормированные антисимметричные по отношению к σ-
и π-электронам функции, соответственно. Их можно разложить по слейтеровским детерминантам,
составленных только из σ- и только из π-МО. Волновая функция ψσ одинакова как для основного, так и для возбужденных состояний и все изменения связываются с π-электронами. В результате размерность уравнений Рутана сильно сокращается: например, для этилена вместо 12 валентных электронов необходимо учитывать только 2 π-электрона.Метод Парризера-Попла-Парра
НДП+π-электронное приближение = метод Парризера-Попла-Парра.
Uμμ = - Iμ , γAА = Iμ - Aμ ( Iμ и Aμ - из спектроскопических данных для для валентных состояний атомов), γAB - по формулам типа Оно.
hμν считаются параметрами и выбираются по разному для расчета свойств основного (метод Попла) и возбужденных (метод Парризера- Парра) состояний.
Для основного состояния hμν = βμν = kSμν, где k подбирается по теплотам образования.
Для возбужденных состояний следует учесть, что волновая функция молекулы должна быть суммой волновых функций основного Ψ0 и возбужденных Ψi→k состояний: Ψ =Ψ0 + ∑аi→kΨi→k.
Слайд 14Обычно учитывают несколько однократно возбужденных электронных конфигураций заданной мультиплетности и
ищут коэффициенты аi→k вариационным методом. Матричные элементы (Ψ0⎪hπ⎪Ψ0) дают энергию
основного состояния Е0, а элементы (Ψi→k⎪hπ⎪Ψj→l) имеют вид:(Ψi→k⎪hπ⎪Ψj→l)≡ hπ i→k, j→l = δ klεk - δ ijεi +2(jk⎪li)-(jk ⎪il).
В приближении НДП
hπ i→k, j→l = δ ij δ kl (εk - εi) +∑[2(1-R)сμj сμl cνi сνk - сμj сμi сνk cνl],
где R=0 для синглетных состояний и R=1 – для триплетных.
Расчет проводится методом ССП: вначале определяют МО для основного состояния, а затем, используя их, строят волновые функции возбужденных состояний.
Метод Парризера-Попла-Парра включает в себя метод КВ и очень хорош как при определении геометрии, потенциалов ионизации и сродства к электрону, так и при расчетах оптических спектров поглощения сопряженных органических молекул. Спектр поглощения состоит из нескольких полос, связанных с определенными электронными переходами. Для плоских молекул МО можно разделить на три группы: σ, π и n*.
Слайд 15 Диагонализизация матрицы hπ i→k, j→l называемой матрицей конфигурационного
взаимодействия, дает энергии спектральных переходов и веса возбужденных конфигураций аi→k.
Ориентированный на π-электроны, метод ППП описывает π-π* переходы с точностью ~ 0,1-0,2 эВ или 3-5% .Наиболее вероятное относительное расположение соответствующих энергетических уровней и разрешенные правилами отбора типы электронных переходов.
Слайд 16 Метод МО Хюккеля
Это не-ССП метод, предложенный для углеводородов
(Хюккель, 1931), основан на нескольких сильных приближениях:
π-электронное приближение; считают,
что АО образуют ортонормальный базис, т.е. Sμν = δμν .Межэлектронными взаимодействиями (т.е. всеми двухэлектронными кулоновскими и обменными интегралами) пренебрегают. Из-за этого решение уравнений метода проводится в один шаг.
3) Матричные элементы оператора Фока оцениваются на основании эмпирической информации и являются фиксированными:
hμμ = αμ ,
hμν = kβμν .
αμ = Iμ - кулоновский интеграл (не путать с γAB!),
4) Принимается, что βμν=0, если АО μ и ν не принадлежат ковалентно связанным атомам.
Соответствующие этим приближениям уравнения Рутана
∑сiμ (hμν - εiδμν ) = 0
называются уравнениями Хюккеля.
Слайд 17 Полная энергия в этом методе есть просто сумма
орбитальных энергий
Е = ∑ni εi , n=0,1 или 2. Уравнения Хюккеля могут быть легко записаны и решены для любой системы.
Пример – расчет молекулы этилена С2Н4 с 2 π-электронами (свяжем их с χ(рz) -АО атомов углерода, направленными перпендикулярно плоскости молекулы). Интегралы αС = -11,0 эВ, βСС –2,4 эВ.
Детерминант, дающий ненулевые решения, имеет вид
(здесь произведена замена х = (αС – ε)/βСС). Раскрывая определитель, имеем
х2 –1 = 0 и х = ± 1, откуда ε1= αС +βСС , ε2 =αС – βСС.
В принятых обозначениях система уравнений Хюккеля имеет вид
с1 х + с2 =0
с1 + с2 х =0,
Подставим сюда х = ± 1.
Слайд 18х= -1 → с1 = с2 . Используя условие нормировки
волновой функции этилена
с12 + с22 =1, имеем с1 =
с2 = 1/√2 и получаем одну из π-МО этилена ϕ1 = 1/√2 (χ1 +χ2).
2) х = 1 → с1 = - с2 и ( аналогично) получаем другую π-МО.
ϕ2 = 1/√2 (χ1 - χ2).
βСС < 0 → ε1 < ε2 , причем, ε1 - ε2 = 2βСС. Это означает, что МО ϕ1 более энергетически стабильна.
Существуют различные модификации метода Хюккеля, касающиеся способа выбора параметров α и β. Этот метод был также распространен на системы с гетероатомами в цикле.
Метод Хюккеля хорошо описывает свойства плоских органических молекул с двойной и тройной связями – полиенов.
Общая формула линейных полиенов. n – длина цепи (порядок полиенов)
Слайд 19Вековое уравнение для таких систем выглядит следующим образом:
Разделив (107) на
β и производя замену (α–Е)/β = –х, получим
Для детерминантов различных
порядков получаем:D1 = –x, D2 = x2–1, D3 = –x3+2x, D4 = –x4–3x2+1,…Dn = –xDn–1–Dn–2.
Полиномы последовательности (108) подобны полиномам Чебышева, что позволяет путем соответствующих преобразований [9] получить следующее выражение для энергии:
Слайд 20Схема π–электронных уровней энергии в зависимости от длины полиеновой цепи
n (расчет методом Хюккеля)
где n – число атомов углерода в
цепи или порядок полиена. Каждое значение j от 1 до n обозначает одно из решений или корней векового уравнения. При n = 2 j = 1, 2 получаем решение (105) (106) для молекулы этилена.Слайд 21Энергетические уровни для циклической системы, включающей n орбиталей, располагаются примерно
также, как и для линейных структур:
, j = 0, ±1, ±2,… Вид образующихся МО циклической системы, представляется уравнением
, , j = 0, ±1, ±2, … .
Электроны распределяются по уровням в соответствии с принципом Паули. Энергия перехода с верхнего занятого уровня на нижний вакантный убывает по мере увеличения n. Уменьшение энергии перехода π → π* с ростом размера молекулы наблюдается экспериментально, что подтверждает предсказательную способность метода Хюккеля для данного класса органических соединений. При n → ∞ уровни энергии сливаются в сплошную зону.
Слайд 22Расширенный метод Хюккеля (Хоффман, 1963)
Идея: оригинальная схема
Хюккеля дополняется рассмотрением всех валентных (а не только π) орбиталей
и явным учетом интегралов перекрывания.Уравнения РМХ формально совпадают с уравнениями Рутана, однако матричные элементы оператора Фока Fμν ≡ hμν являются параметрами и наиболее часто оцениваются следующим образом:
hμμ = - Iμ. ,
hμν = 0.5K(hμμ + hνν).
В варианте Вольфсберга-Гельмгольца К=1,75. Интегралы перекрывания вычисляются аналитически с ОСТ.
РМХ-энергия молекулы с закрытой оболочкой
Е= 2( ∑∑ с2iμ hμμ + ∑∑∑ сiμ сiν hμν),
(члены, ответственные за межэлектронное и межъядерное взаимодействие, не учитываются).
В системах с равномерным распределением электронов выражение РМХ дает хорошие относительные оценки энергии в рядах соединений. Гетероатомы нарушают равномерность электронного распределения и РМХ здесь часто непригоден. Тем не менее, РМХ дает зачастую лучшие результаты, чем его простой аналог, при изучении конформаций циклических молекул, барьеров внутреннего вращения, относительный порядок уровней энергии.
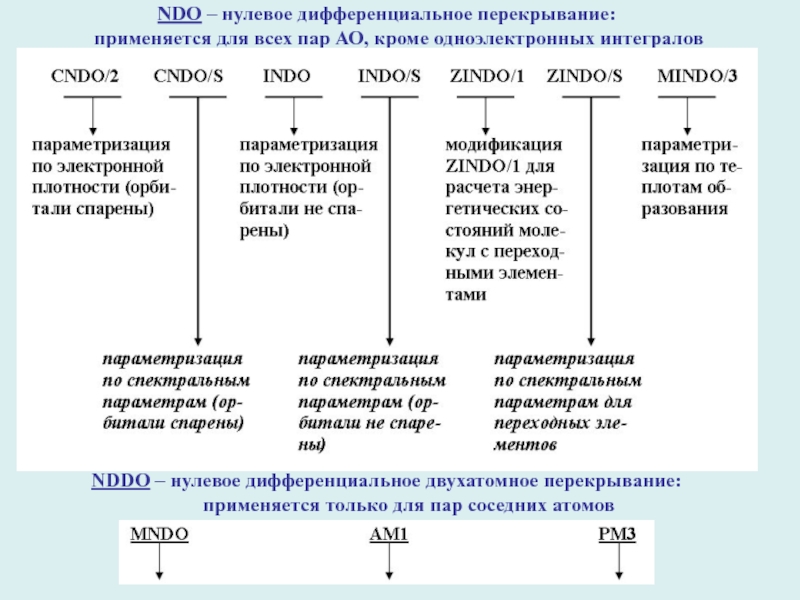
Слайд 23NDO – нулевое дифференциальное перекрывание:
применяется для всех
пар АО, кроме одноэлектронных интегралов
NDDO – нулевое дифференциальное двухатомное
перекрывание: применяется только для пар соседних атомов
Слайд 25Точность квантово-химических расчетов свойств молекул
а)Точность неэмпирического расчета
Ошибки
всех неэмпирических квантово-химических методов возрастают при использовании «коротких» базисных наборов.
Оценки точности ХФ или МР2 для органических молекул в базисах, не хуже чем DZP или 6-31G*, следующие:- длины связей 0.01 - 0.02 А ( для элементо- и металлоорганических соединений несколько хуже);
-электронная плотность -10%, длины связей и валентные углы - ~ 1 %;
-энергии конформационных переходов (вращение и барьеры инверсии) - < 2 ккал/моль (использование широкого базиса обязательно);
- ХФ - частоты колебаний для большинства ковалентных связей систематически завышены на 10-12 % из-за пренебрежения электронной корреляцией и ангармонизмом (очень низкие частоты колебаний имеют более высокие ошибки): шкалирующий множитель 0.89 ± 0.01 позволяет получить прекрасное согласие с экспериментом. МР2 приводит к таким же результатам без шкалировки;
- энергии нулевых колебаний ~ 1 ккал/моль;
- энергии изодесмических реакций - 2-4 ккал/моль;
Слайд 26-энтропии ~ 0.5 энтропийной единицы (ккал/К моль);
-присоединение/отщепление протона (с использованием
смешанного базиса, с включением аниона) - ~ 10 ккал/моль (в
газовой фазе);- реакции атомизации и гомолитического разрыва связи - большая ошибка (25-40 ккал/моль);
-Барьеры активации реакций - большие ошибки.
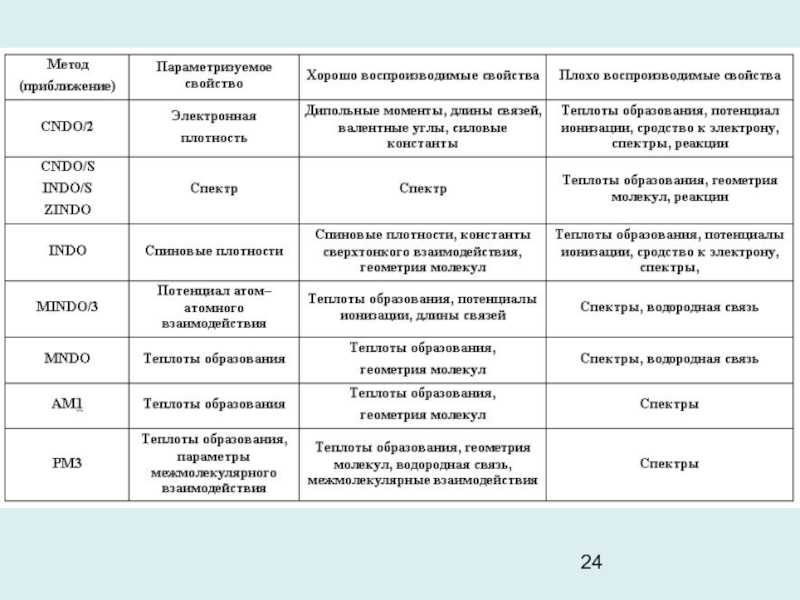
б)Точность полуэмпирических методов
Полуэмпирические методы параметризуются так, чтобы воспроизводить те или иные свойства молекул. Поэтому расчет всех свойств на основании одного набора параметров надежным признан быть не может. Это общий и наиболее существенный недостаток полуэмпирической квантовой химии.
Для молекул с закрытыми оболочками метод MNDO с параметризациями AM1 и PM3 дает хорошие результаты для молекулярной структуры и теплоты образования. Средняя абсолютная ошибка для неводородных атомов в PM3 составляет 0.036 А; она несколько больше в AM1. Ошибки в валентных углах равны 3-4 градуса (хуже, чем в неэмпирических расчетах низкого уровня).
Слайд 27 Ошибка расчета энергии образования органических молекул и переходных
состояний органических реакций (PM3) < 5 ккал/моль.
Точность
оценки синглет-синглетных π-π* переходов методом ППП составляет 0,1-0,2 эВ (3-5%). Для расчета σ-π* и n-π* переходов используется метод CNDO/S, дающий ошибку ~ 10%. Полуэмпирические методы выявляют тенденции в колебательных частотах в рядах близких соединений, однако ошибки не носят систематический характер и поэтому их не удается скорректировать.