Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОЛУПРОВОДНИКОВЫЕ И ОПТОВОЛОКОННЫЕ ЛАЗЕРЫ
Содержание
- 1. ПОЛУПРОВОДНИКОВЫЕ И ОПТОВОЛОКОННЫЕ ЛАЗЕРЫ
- 2. Нерегулярные ОВОсновные определенияВремя прохождения лучаКонусные переходы и
- 3. Основные определенияДля ввода излучения в световоды используют
- 4. Основные определенияИсключая из соотношений (Ф. – 35,36с),
- 5. Время прохождения луча В нерегулярном световоде локальная
- 6. Время прохождения лучаТогда время прохождения однородного участка
- 7. Время прохождения лучаЕсли теперь учесть ранее доказанное
- 8. Время прохождения луча. Случай нерегулярного ОВ
- 9. Время прохождения луча. Случай нерегулярного ОВ
- 10. Концентраторы светового излученияКонусные переходы и фокусировка света
- 11. Возбуждение коллимированным пучком. Параболический переходРассмотри случай, когда
- 12. Возбуждение коллимированным пучком. Линейный переходПусть линейный переход,
- 13. Возбуждение коллимированным пучком. Линейный переходЭквивалентный геометрический путь
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Нерегулярные ОВ
Основные определения
Время прохождения луча
Конусные переходы и фокусировка света
Возбуждение
коллимированным пучком. Параболический переход
– ОВ со ступенчатым профилем показателя преломления, сердцевина которого имеет переменный радиус (полупериод zp(z) траектории направляемых лучей изменяется вдоль оси)Слайд 3Основные определения
Для ввода излучения в световоды используют ОВ с изменяющимся
от z показателм преломления n(z).
В этом случае уже нет лучевого
инварианта, но можно по аналогии определить лучевую функцию:
(Ф. - 35)
Для случая ОВ с изменяющимся от z показателем преломления и с круговой симметрией уравнения лучевой траектории запишутся, как
(Ф. - 36)
Слайд 4Основные определения
Исключая из соотношений (Ф. – 35,36с), получим уравнение для
лучевой функции:
(Ф. - 37)
где r(z) вычисляется вдоль лучевой траектории. Решение
этого уравнения имеет вид:
(Ф. - 38)
где - исходное значение лучевой функции в начале ОВ. Интегрирование выполняется вдоль лучевой траектории.
Для ОВ с круговой симметрией существует инвариант . Его можно получить, умножив уравнение (Ф. – 36b) на r2 и проинтегрировав:
(Ф. - 39)
Используя выражение (Ф. – 39) можно исключить в (Ф. – 36а) d/ds. Решение (Ф. – 36а) позволяет найти уравнение лучевой траектории r(z).
Слайд 5Время прохождения луча
В нерегулярном световоде локальная скорость света составляет
c/n(r,z). Поэтому время прохождения луча участка ОВ длиной z:
(Ф. -
40)
Важный для практики случай, когда профиль показателя преломления меняется вдоль z настолько медленно, что практически постоянен на расстояниях zp, равных полупериоду луча, так что (см. рис.7.2 и рис.7.3)
Если условия медленного изменения выполнены, то можно построить приближенную модель нерегулярного ОВ, разбивая его (рис.7.3) на ряд регулярных участков. Каждый участок имен длину zp(z), равную полупериоду траектории луча, и для удобства считается, что радиус (z) и профиль показателя преломления n(r,z) участка совпадают с соответствующими значениями в его средней точке.
Рис.7.2. – ОВ с постоянными показателями преломления сердцевины и оболочки, но с радиусом медленно меняющемся на полупериоде лучевой траектории
Рис.7.3. – медленно изменяющийся ОВ и его приближенная модель из набора однородных участков
Слайд 6Время прохождения луча
Тогда время прохождения однородного участка длиной zp(z) равно
tp(z) = L0(z)/c, где L0(z)/ - длина оптического пути:
(Ф. - 41)
Лучевые траектории
в медленно изменяющихся оптических волноводах (МИОВ) характеризуется двумя масштабами – быстрым и медленным.Быстрый масштаб равен лучевому полупериоду zp(z).
Медленный масштаб характеризует нерегулярность, которая существенна только на расстояниях, больших полупериода.
Изменение показателя преломления в радиальном направлении гораздо более быстрое, чем в продольном: .
В такой ситуации мы можем усреднить быстрое изменение по лучевому полупериоду, в пределах которого ОВ рассматривается как аксиально регулярный. Математически это эквивалентно замене подынтегрального выражения его средним значением по полупериоду:
(Ф. - 42)
где для ясности использована переменная интегрирования , чтобы различать аксиальное расстояние в локально регулярном ОВ и расстояние z вдоль нерегулярного световода.
Слайд 7Время прохождения луча
Если теперь учесть ранее доказанное выражение, связывающее дифференциалы
координат оси и радиуса
, то из (Ф.-41) следует, что(Ф. - 43)
По тем же соображениям мы можем провести усреднение в уравнении для лучевой функции (Ф. - 37):
(Ф. - 44)
Слайд 8Время прохождения луча.
Случай нерегулярного ОВ с усеченным степенным профилем
Рассмотрим
важный для практики случай нерегулярного ОВ с усеченным степенным профилем.
(Ф.
- 45)
Вводя в полученное ранее выражение для времени прохождения луча зависимости соответствующих величин от z, получим для анализируемого случая:
(Ф. - 46)
Слайд 9Время прохождения луча.
Случай нерегулярного ОВ с усеченным степенным профилем
Можно
показать [Снайдер], что для нерегулярного ОВ с медленно меняющимся вдоль
оси усеченным ступенчатым профилем лучевой параметр удовлетворяет уравнению(Ф. - 47)
Для практики самые важные случаи: q = 2 (параболический профиль) и q = (ступенчатый профиль). Для ступенчатого профиля (Ф. - 47) с учетом определения лучевого параметра (Ф. - 35) после очевидных преобразований дает:
(Ф. - 48)
Это важное выражение для оценок распространения лучей в ОВ с изменяющимся радиусом сердцевины.
Слайд 10Концентраторы светового излучения
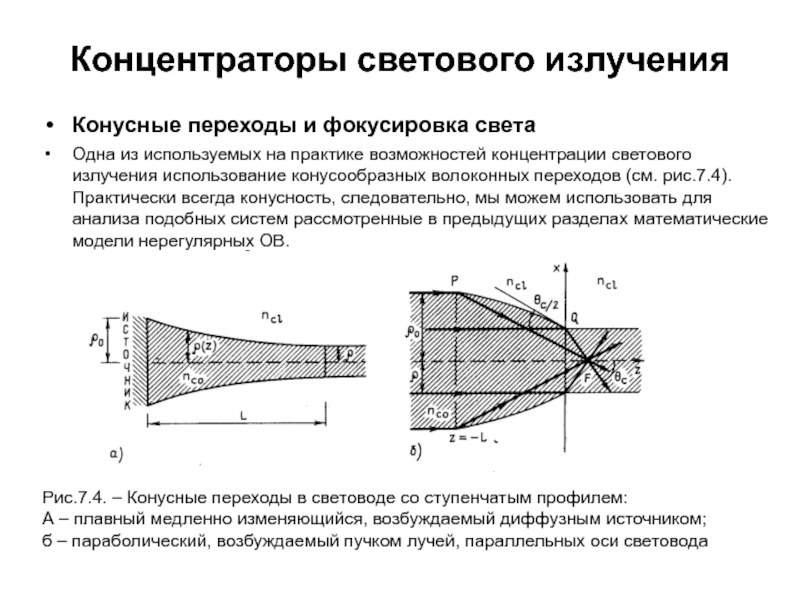
Конусные переходы и фокусировка света
Одна из используемых
на практике возможностей концентрации светового излучения использование конусообразных волоконных переходов
(см. рис.7.4). Практически всегда конусность, следовательно, мы можем использовать для анализа подобных систем рассмотренные в предыдущих разделах математические модели нерегулярных ОВ.Рис.7.4. – Конусные переходы в световоде со ступенчатым профилем:
А – плавный медленно изменяющийся, возбуждаемый диффузным источником;
б – параболический, возбуждаемый пучком лучей, параллельных оси световода
Слайд 11Возбуждение коллимированным пучком. Параболический переход
Рассмотри случай, когда коллимированный пучок падает
строго вдоль оси ступенчатого параболического конусного перехода (рис.). В координате
z = -L он примыкает к световоду с радиусом 0 , а в координате z = 0 к ОВ с радиусом сердцевины . Считаем далее, что всюду сердцевина имеет один и тот же показатель преломления nco, а показатели преломления оболочек всюду равны ncl.Хорошо известно, что параллельные лучи падающие на параболическую поверхность фокусируются в одной точке. Минимальная длина перехода, при которой вся световая мощность попадающая в переход, возбуждает только направляемые лучи, определяется из условия: луч, отраженный в точке Q, должен образовывать с осью ОВ угол c. Из рис очевидно, что угол между падающим лучом и касательной к границе сердцевины в точке Q равен c/2.
Граница параболического перехода относительно оси задается уравнением:
(Ф. - 49)
Если потребовать, чтобы в сечении z = 0 выполнялось условие dx/dz = tg(c/2), то
(Ф. - 50)
Приближенное выражение справедливо для слабонаправляющего ОВ, т.е. при c << 1.
Слайд 12Возбуждение коллимированным пучком. Линейный переход
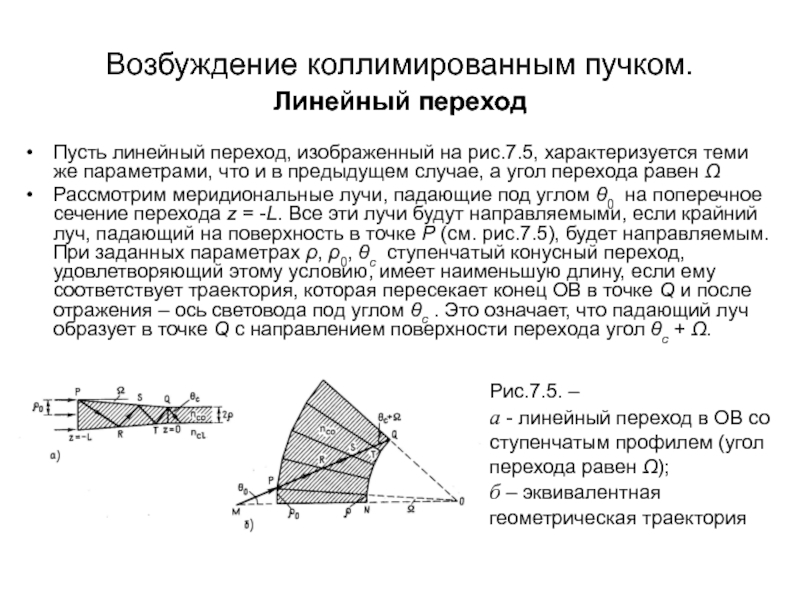
Пусть линейный переход, изображенный на рис.7.5,
характеризуется теми же параметрами, что и в предыдущем случае, а
угол перехода равен Рассмотрим меридиональные лучи, падающие под углом 0 на поперечное сечение перехода z = -L. Все эти лучи будут направляемыми, если крайний луч, падающий на поверхность в точке P (см. рис.7.5), будет направляемым. При заданных параметрах , 0, c ступенчатый конусный переход, удовлетворяющий этому условию, имеет наименьшую длину, если ему соответствует траектория, которая пересекает конец ОВ в точке Q и после отражения – ось световода под углом c . Это означает, что падающий луч образует в точке Q с направлением поверхности перехода угол c + .
Рис.7.5. –
а - линейный переход в ОВ со ступенчатым профилем (угол перехода равен );
б – эквивалентная геометрическая траектория
Слайд 13Возбуждение коллимированным пучком. Линейный переход
Эквивалентный геометрический путь луча. Для лучевой
траектории, изображенной на рис. можно изобразить эквивалентную схему, в которой
ломаная траектория заменяется прямой (рис. ). OQ = ON = /tg , OM = ON + L +0/tg0. Применяя теорему синусов к треугольнику QOM, выразим и, следовательно, Lmin через , 0, c .(Ф. - 51)
При малых углах
(Ф. - 52)
Из сопоставления (Ф. - 50) и (Ф. - 52) видно, что минимальная длина параболического перехода больше, чем у соответствующего линейного перехода в (0 + )/(0 - ) раз для малых углов конусности и слабонаправляющих ОВ.








![ПОЛУПРОВОДНИКОВЫЕ И ОПТОВОЛОКОННЫЕ ЛАЗЕРЫ Время прохождения луча. Случай нерегулярного ОВ с усеченным степенным профилемМожно показать Время прохождения луча. Случай нерегулярного ОВ с усеченным степенным профилемМожно показать [Снайдер], что для нерегулярного ОВ](/img/thumbs/2152b98fe1934257e06ceb60c19f3725-800x.jpg)