Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие и свойства алгоритма
Содержание
- 1. Понятие и свойства алгоритма
- 2. Понятие алгоритмаАлгоритм – последовательность действий (план) для
- 3. Свойства алгоритмовДискретность – алгоритм состоит из набора
- 4. Основные этапы технологического процесса решения задач с
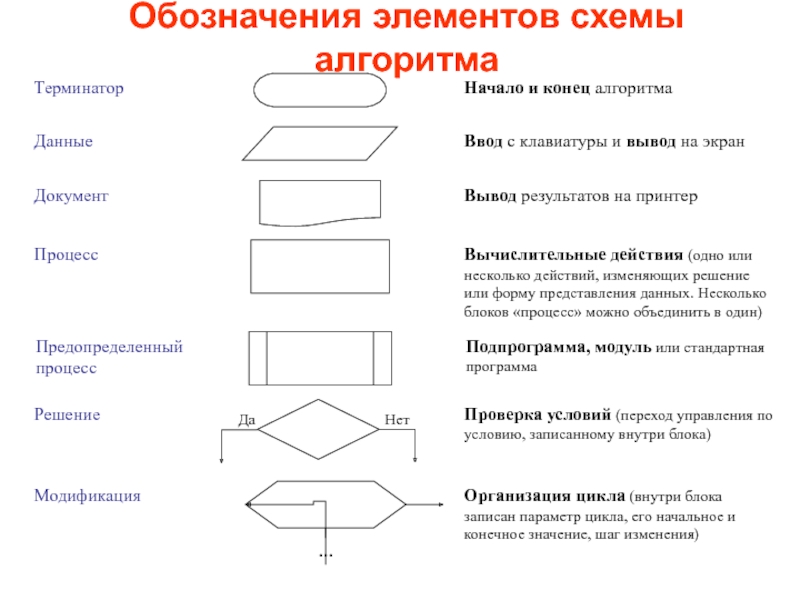
- 5. Основные правила оформления схемы алгоритмаСимвол предназначен для
- 6. Обозначения элементов схемы алгоритма
- 7. Виды алгоритмов Алгоритмы линейной структуры (линейные алгоритмы)
- 8. Пример линейного алгоритма: Вычисление площади круга1 этап:
- 9. Типы ветвящихся алгоритмовдва альтернативных вариантамноговариантный выбор
- 10. Пример 1 ветвящегося алгоритма: Решение квадратного уравнения1
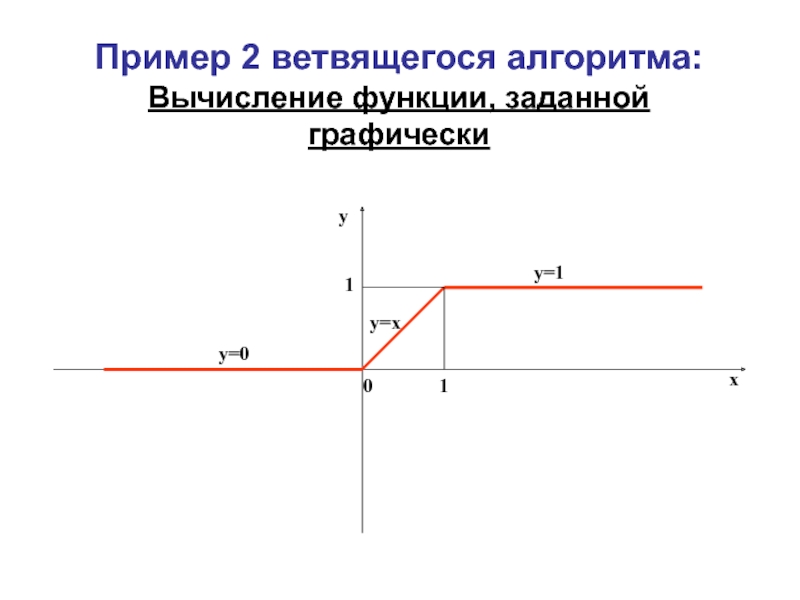
- 11. Пример 2 ветвящегося алгоритма: Вычисление функции, заданной графически0xyy=0y=1y=x
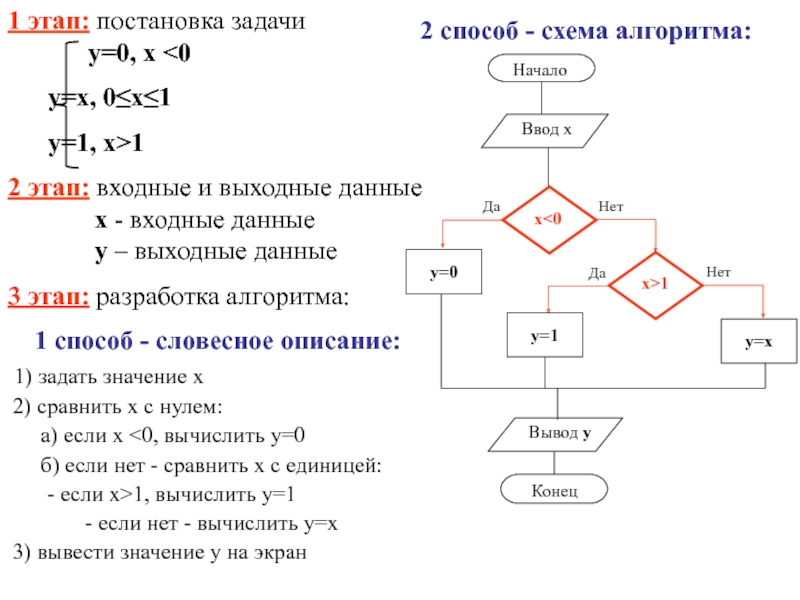
- 12. 2 способ - схема алгоритма:
- 13. Пример 3 ветвящегося алгоритма: Организация меню
- 14. 1 этап: постановка задачи -
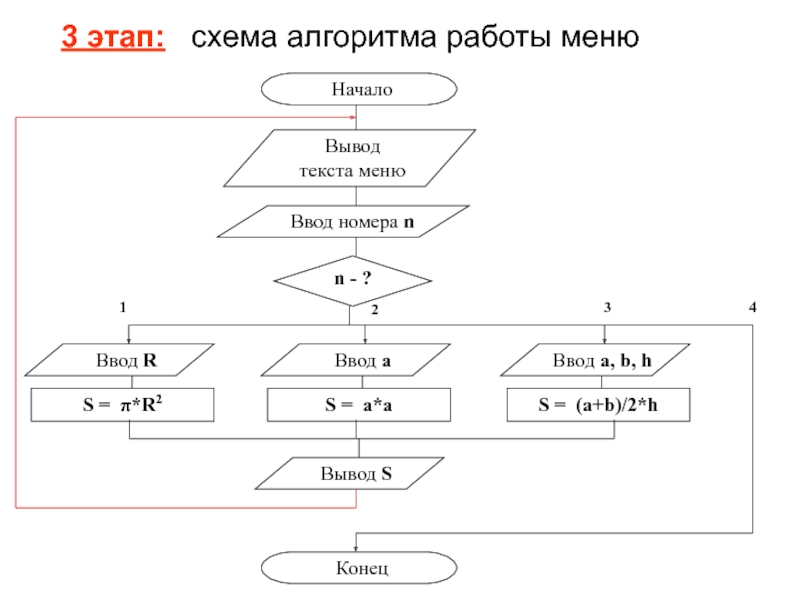
- 15. 3 этап: схема алгоритма работы меню1243
- 16. Циклические алгоритмыОрганизационно цикл состоит из следующих компонентов:
- 17. Пример 1 циклического алгоритма: Вычисление таблицы значений
- 18. 3 типа циклических алгоритмов:1. Цикл с постусловием2. Цикл с предусловием3. Цикл со счетчиком
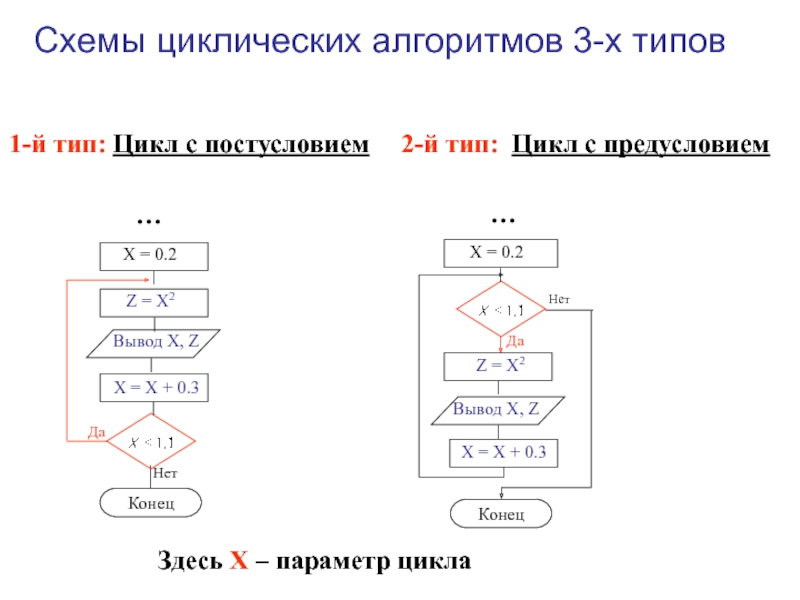
- 19. 1-й тип: Цикл с постусловием2-й тип: Цикл
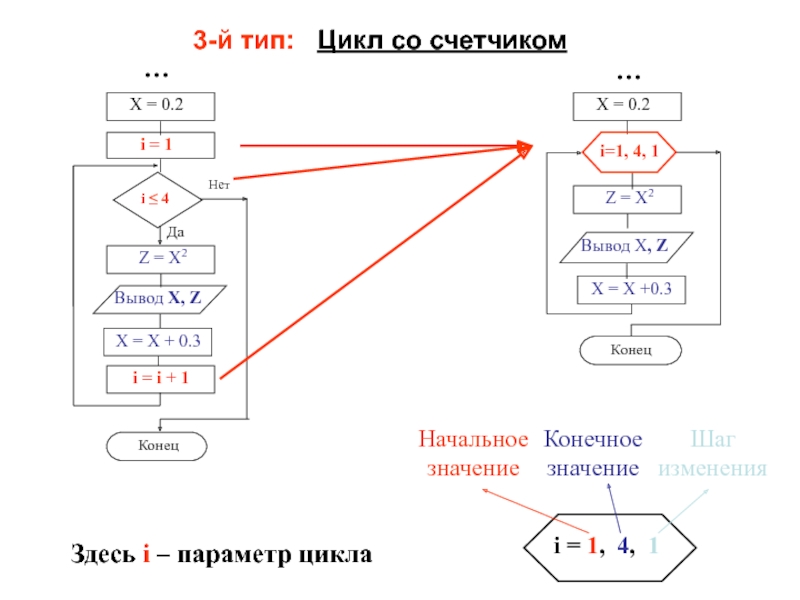
- 20. 3-й тип: Цикл со счетчикомЗдесь i – параметр цикла……
- 21. Пример 2 циклического алгоритма (без организации массива)1
- 22. Цикл с постусловиемЦикл с предусловием2 варианта схемы
- 23. Массивы Типовые алгоритмы по обработке одномерных массивов
- 24. Понятие массива Массив – это конечная,
- 25. Размер и размерность массиваРазмер – это количество
- 26. Обозначения 1-мерных массивовСловесное описание: Например,
- 27. Распределение ОЗУ (1-мерные массивы)1. Массив А:2. Массив
- 28. Стандартные алгоритмы для обработки одномерных массивовНахождение суммы
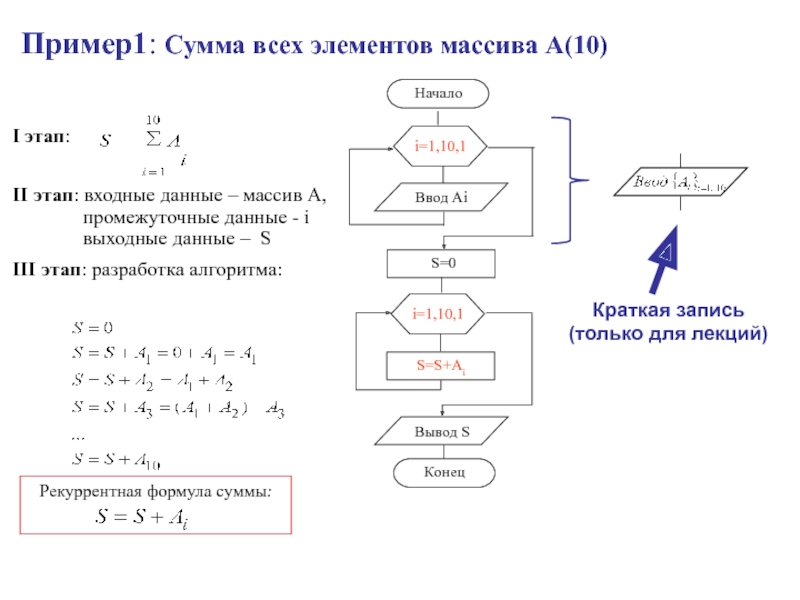
- 29. Пример1: Сумма всех элементов массива А(10)Рекуррентная формула суммы:Ввод Аi
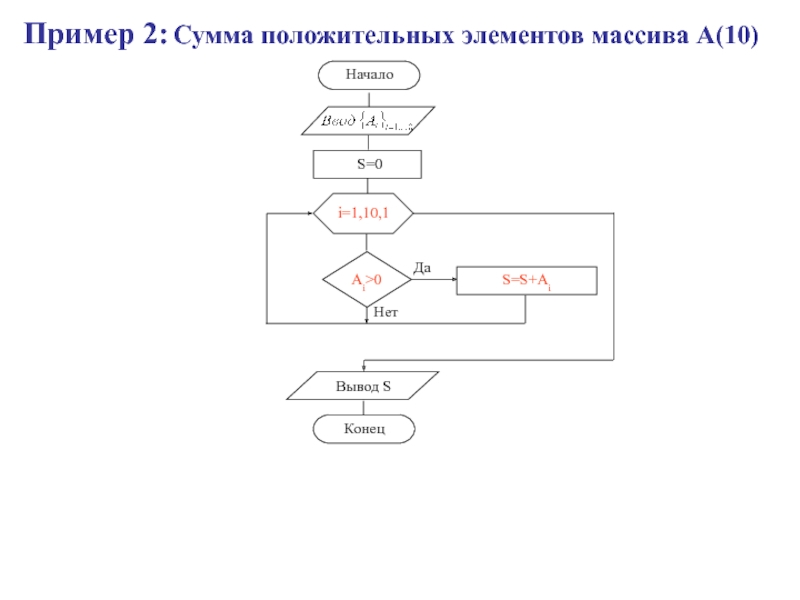
- 30. Пример 2: Сумма положительных элементов массива А(10)
- 31. Пример 3: Произведение всех элементов массива А(10)II
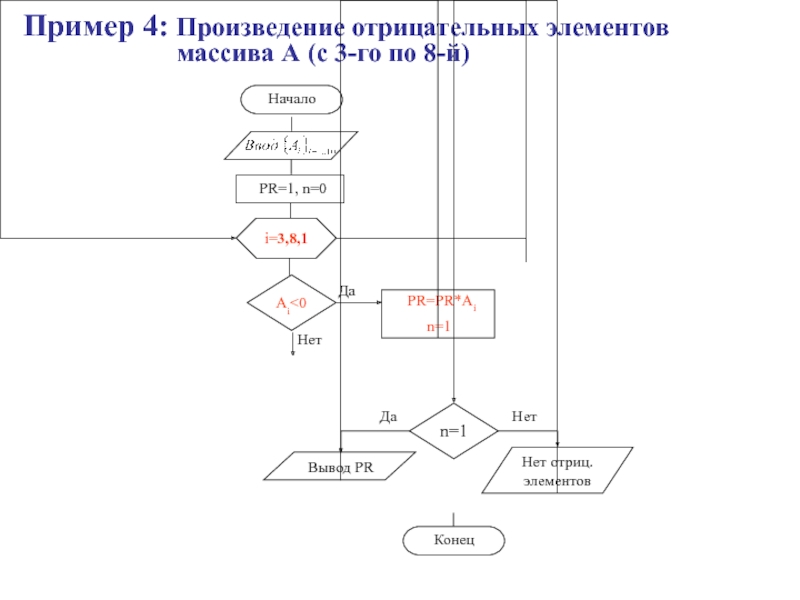
- 32. Пример 4: Произведение отрицательных элементов
- 33. Пример 5: Максимальный элемент массива АПримечание: Можно ввести следующие дополнительные проверки: единственность максимума все элементы равны
- 34. Сортировка элементов массиваАлгоритмы выбораАлгоритмы обмена
- 35. Алгоритм выбораИсходный массив: 5 4 1 3
- 36. Пример сложного цикла, где во внутреннем цикле
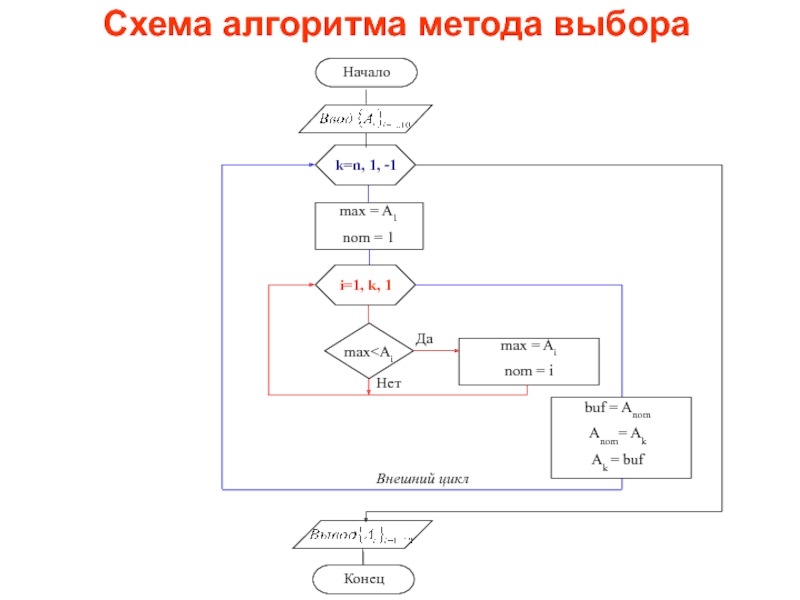
- 37. Схема алгоритма метода выбора
- 38. Алгоритм обменаИсходный массив: 5 4 1 3
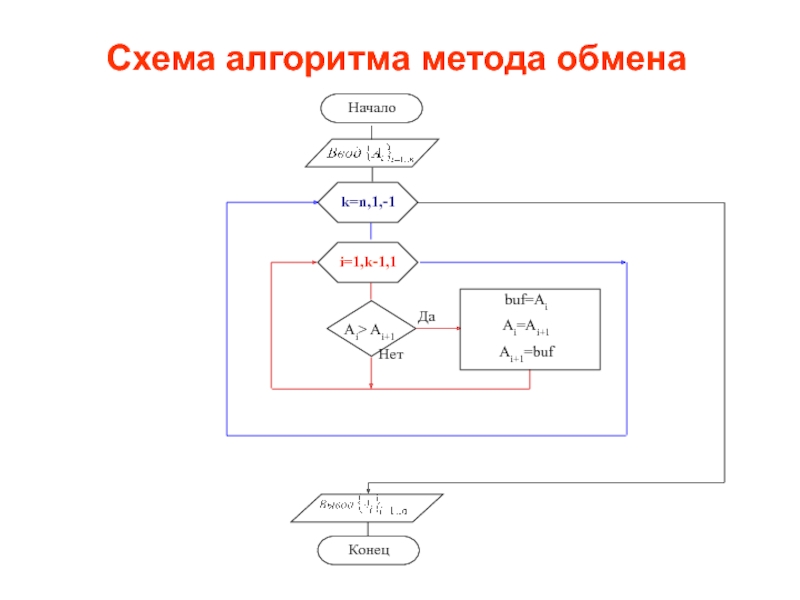
- 39. Схема алгоритма метода обмена
- 40. Двумерные массивы(матрицы) Типовые алгоритмы обработки матриц
- 41. Замечание. 1. Размерность массива А равна 2.
- 42. Пример обозначения 2-мерных массивов Замечание. 1.
- 43. Распределение ОЗУ (матрицы)Матрица А(3х4) :Номера ячеек:
- 44. Стандартные алгоритмы для обработки матрицВычисление суммы элементов
- 45. Ввод и вывод элементов матрицы А(3х4)Вывод элементовВвод элементовКраткая запись (только для лекций):
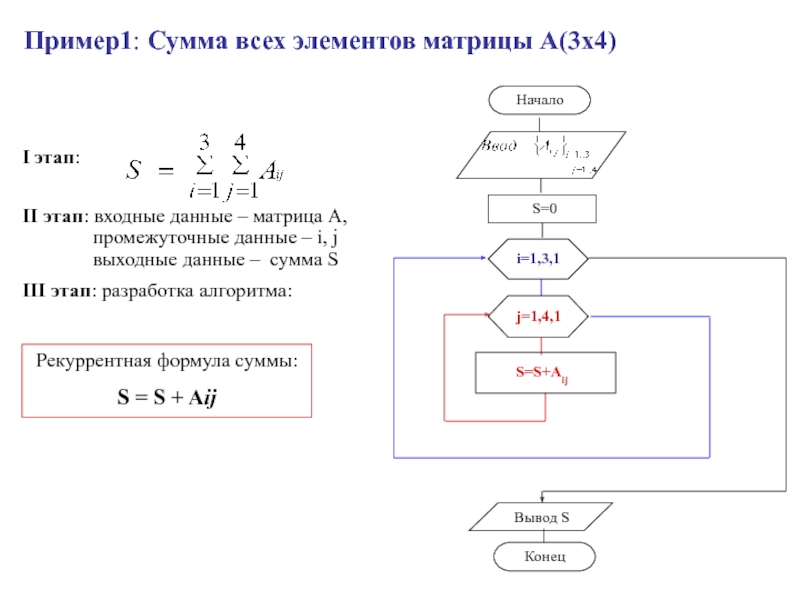
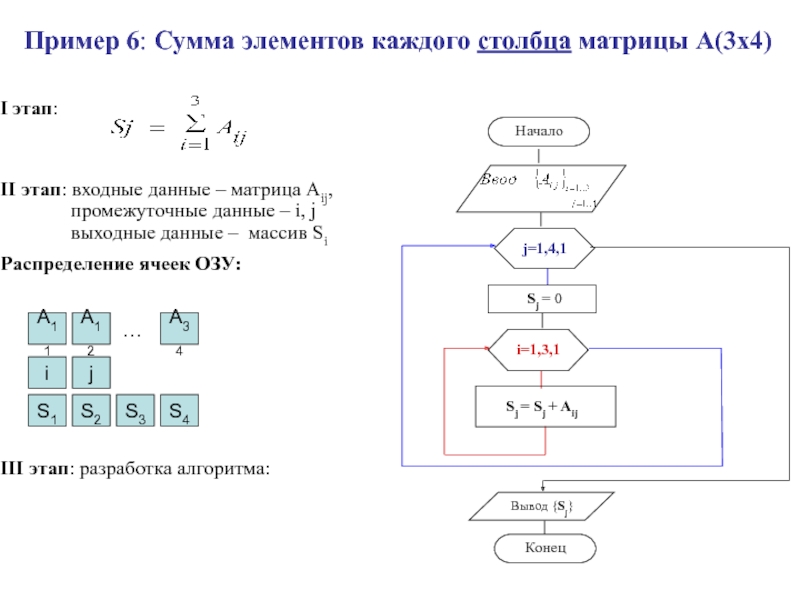
- 46. Пример1: Сумма всех элементов матрицы А(3х4)Рекуррентная формула суммы:S = S + Aij
- 47. Пример 2: Сумма положительных элементов матрицы А(3х4)
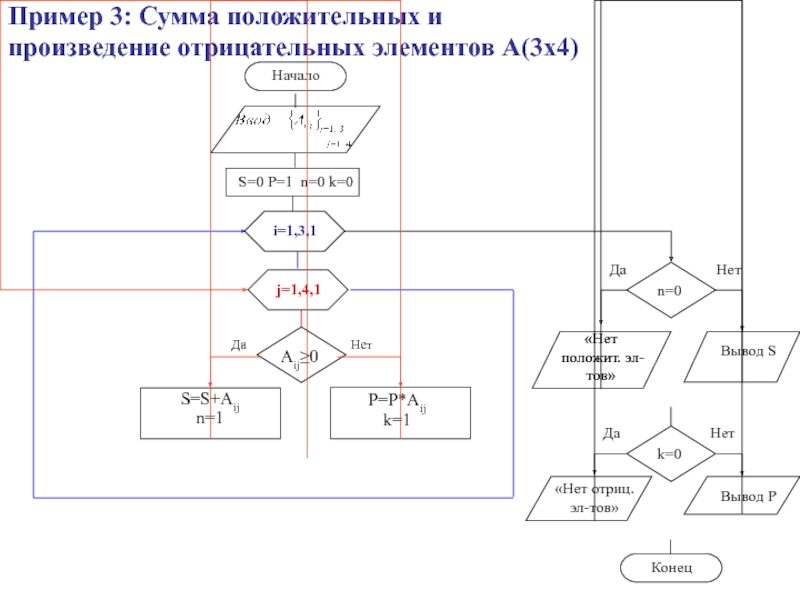
- 48. Пример 3: Сумма положительных и произведение отрицательных элементов А(3х4)
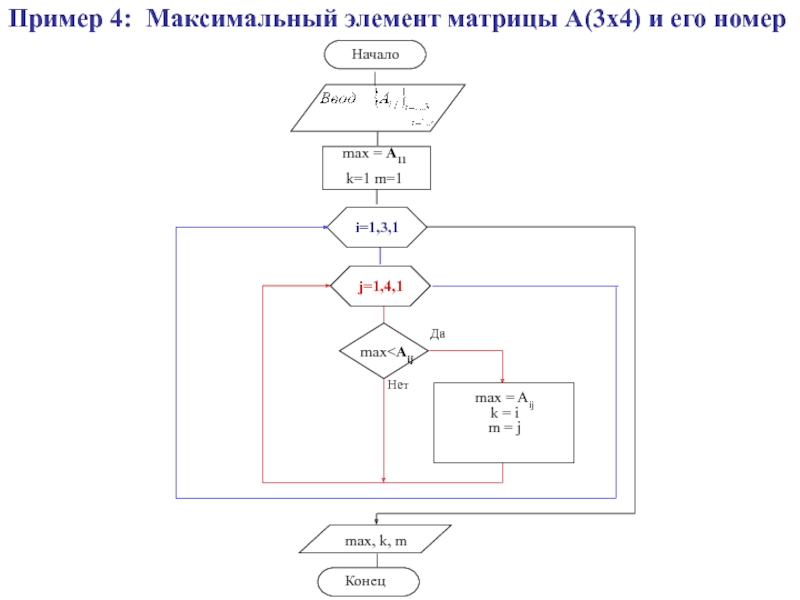
- 49. Пример 4: Максимальный элемент матрицы А(3х4) и его номер
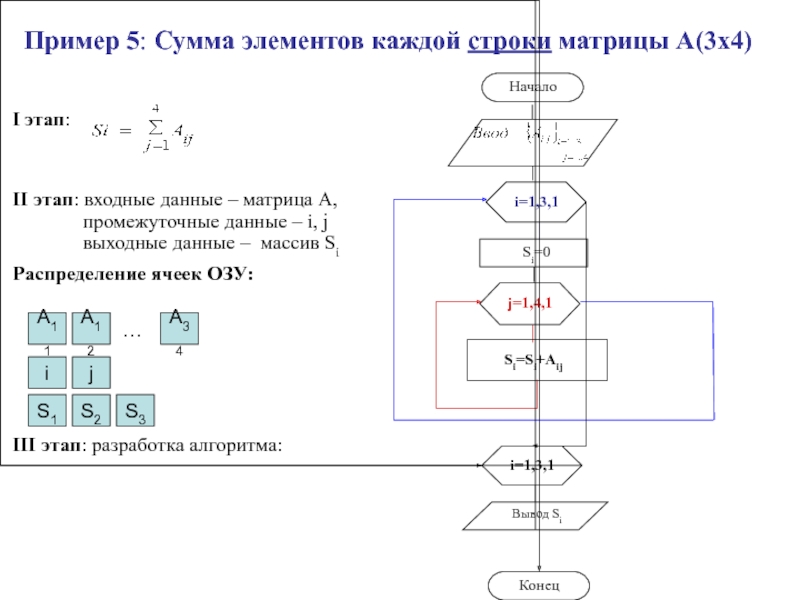
- 50. Пример 5: Сумма элементов каждой строки матрицы А(3х4)
- 51. Пример 6: Сумма элементов каждого столбца матрицы А(3х4)
- 52. Пример 7: Формирование одномерного массива С из
- 53. Алгоритмы обработки квадратных матрицЛекция № 6
- 54. Квадратные матрицыЧисло строк = числу столбцов
- 55. Замечание. 1. Размерность массива K равна 2.
- 56. Стандартные алгоритмы для обработки квадратных матрицВычисление суммы,
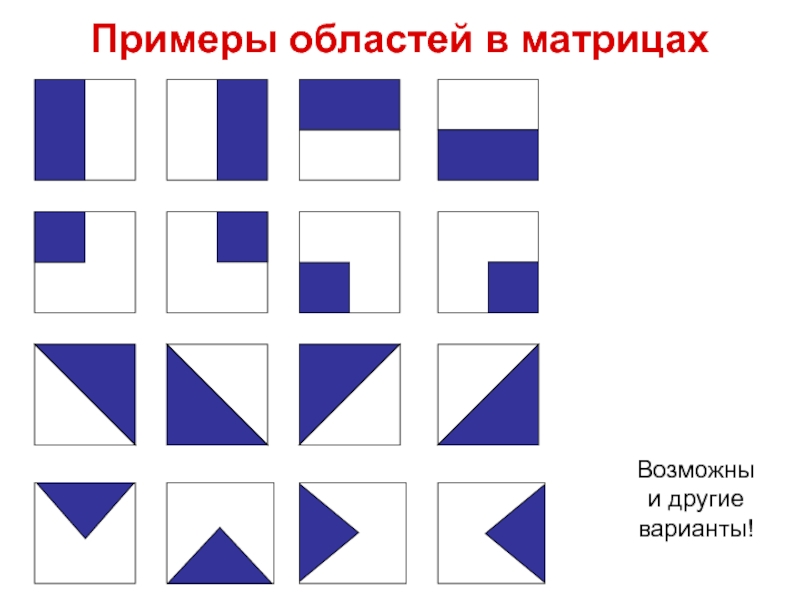
- 57. Примеры областей в матрицахВозможны и другие варианты!
- 58. Определение областейА11 А12 А13 А14 А15А21 А22
- 59. А11 А12 А13 А14 А15А21 А22 А23
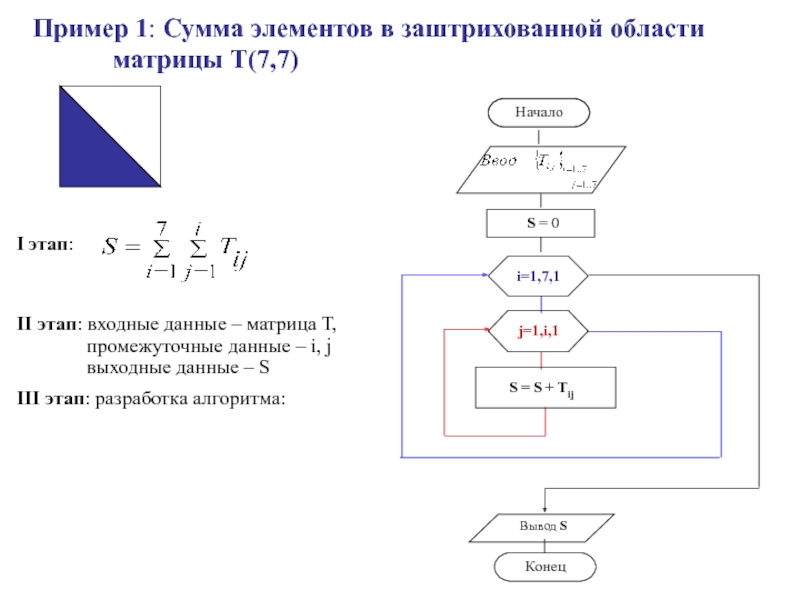
- 60. Пример 1: Сумма элементов в заштрихованной области матрицы Т(7,7)
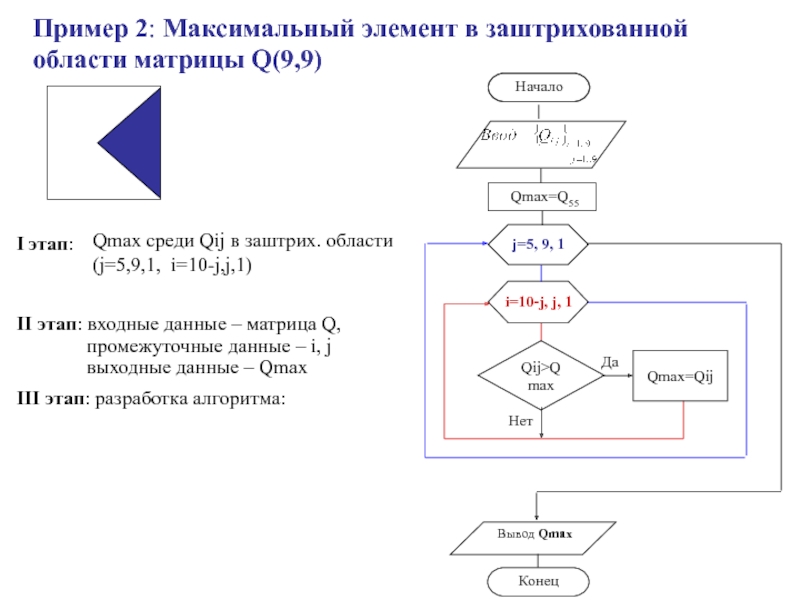
- 61. Пример 2: Максимальный элемент в заштрихованной области матрицы Q(9,9)Qij>Qmax
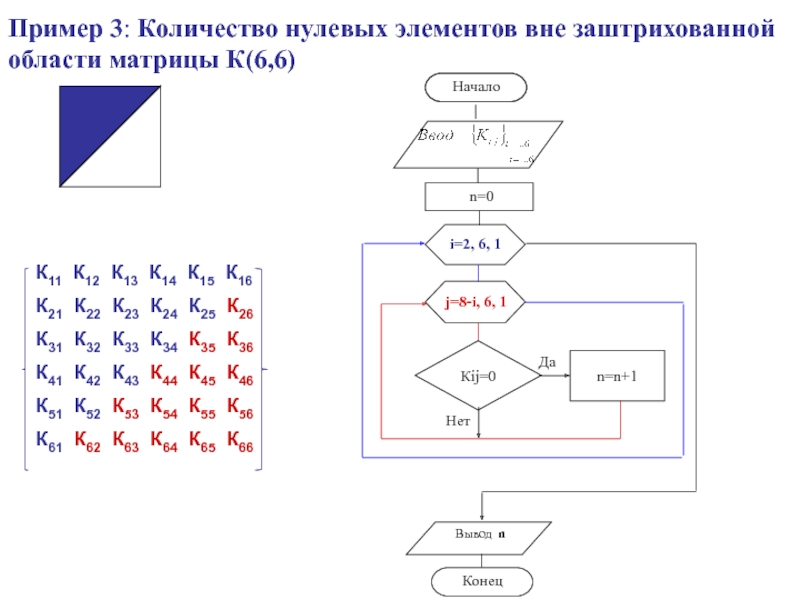
- 62. Пример 3: Количество нулевых элементов вне заштрихованной области матрицы К(6,6)Кij=0
- 63. Пример 4: Сформировать одномерный массив D из
- 64. Схема алгоритма:Xij>0ДаDj=Dj+1Dj=0Вывод Dj
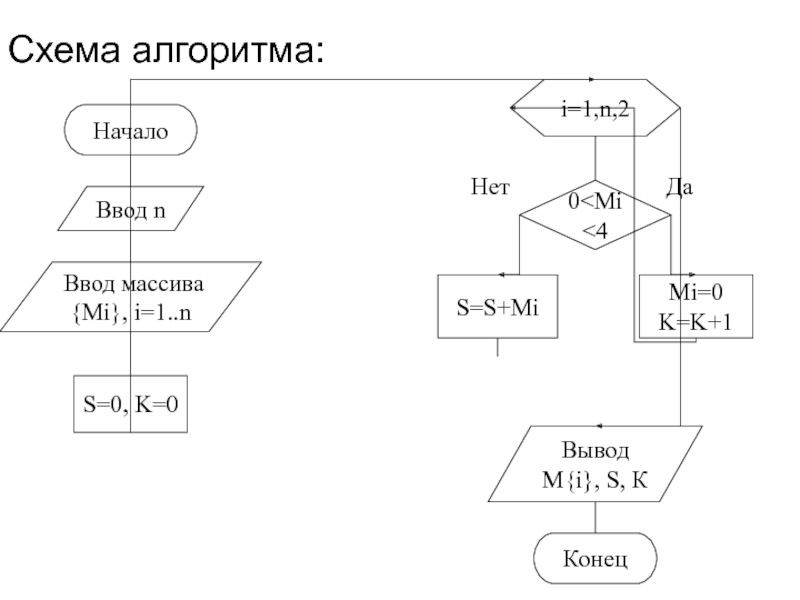
- 65. Чтение алгоритмов
- 66. ПримерДано:Схема алгоритмаВходной поток данных: 8 -4 -1
- 67. Ввод nВвод массива {Mi}, i=1..nS=0, K=0i=1,n,20
- 68. Подход к решениюОпределить тип задачи (сумма, произведение,
- 69. Решение1. Сформулировать постановку задачиВвести массив заданного размера.Среди
- 70. 2. Нарисовать все состояния ячеек ОЗУПервоначальноВвод массиваНачальные значения переменных S и K
- 71. Было перед основным цикломОсновной
- 72. 3. Определить значения выходных данныхВыходные данные:{Mi}:
- 73. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Понятие алгоритма
Алгоритм – последовательность действий (план) для достижения цели за
конечное число шагов
Слайд 3Свойства алгоритмов
Дискретность – алгоритм состоит из набора отдельных законченных действий
(шагов)
Детерминированность / определенность - любое действие алгоритма должно быть строго
и недвусмысленно определено в каждом случаеУниверсальность / массовость - один и тот же алгоритм можно использовать с разными исходными данными
Результативность / конечность - при точном исполнении всех предписаний алгоритма процесс должен прекратиться за конечное число шагов с получением определенного ответа на вопрос задачи (либо вывода о том, что решения не существует)
Слайд 4Основные этапы технологического процесса
решения задач с помощью ЭВМ
1 этап: Постановка
задачи и выбор метода решения
(формальное математическое описание алгоритма)2 этап: Определение и описание входных, промежуточных и выходных данных, необходимых для решения задач.
3 этап: Разработка алгоритма решения задач.
4 этап: Кодирование описания данных и алгоритма (составление программы на выбранном языке программирования).
5 этап: Отладка и тестирование программы с целью её проверки и доведения её в соответствии с поставленной задачей.
6 этап: Выполнение и поддержка программы (создание новых версий в зависимости от новой техники).
Слайд 5Основные правила оформления схемы алгоритма
Символ предназначен для графической идентификации функции,
которую он отображает, независимо от текста внутри этого символа.
Стандартное направление
линий - слева направо и сверху вниз. Пересечение и ветвление линий не допускается. Стрелки на прямых линиях можно не ставить. Если направление отличается от стандартного, то стрелки обязательны.
Линии должны подходить к символу слева, либо сверху, а исходить справа, либо снизу.
Допускается один вход и один выход из символа – кроме символов Модификация и Решение.
ГОСТ 19.701-90 «Схемы алгоритмов, программ, данных, систем»
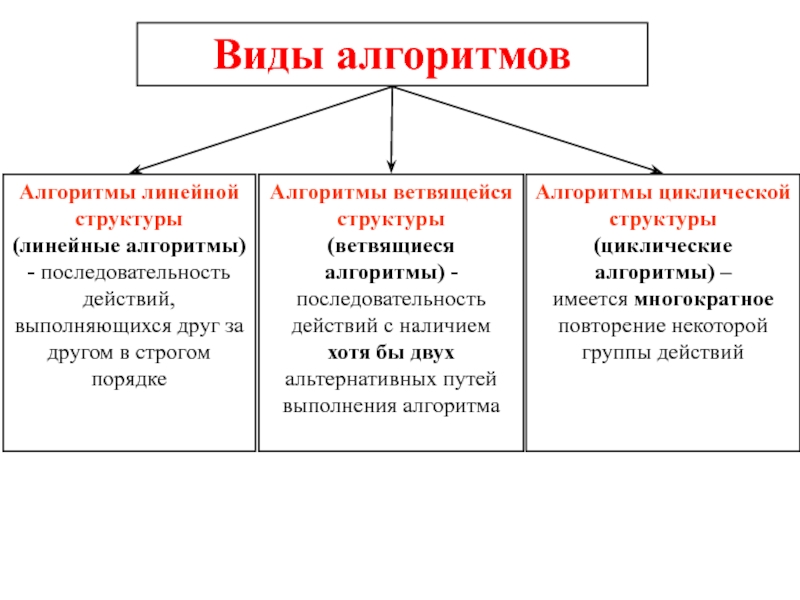
Слайд 7Виды алгоритмов
Алгоритмы линейной структуры
(линейные алгоритмы) - последовательность действий, выполняющихся
друг за другом в строгом порядке
Алгоритмы ветвящейся структуры
(ветвящиеся алгоритмы) -
последовательность действий с наличием хотя бы двух альтернативных путей выполнения алгоритмаАлгоритмы циклической структуры
(циклические алгоритмы) –
имеется многократное повторение некоторой группы действий
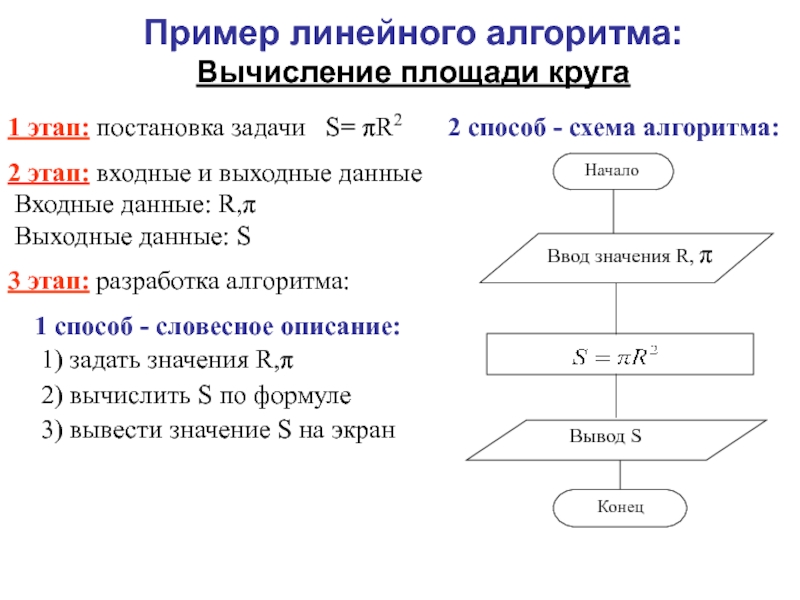
Слайд 8Пример линейного алгоритма:
Вычисление площади круга
1 этап: постановка задачи S=
πR2
2 этап: входные и выходные данные
Входные данные: R,π
Выходные
данные: S3 этап: разработка алгоритма:
1 способ - словесное описание:
1) задать значения R,π
2) вычислить S по формуле
3) вывести значение S на экран
2 способ - схема алгоритма:
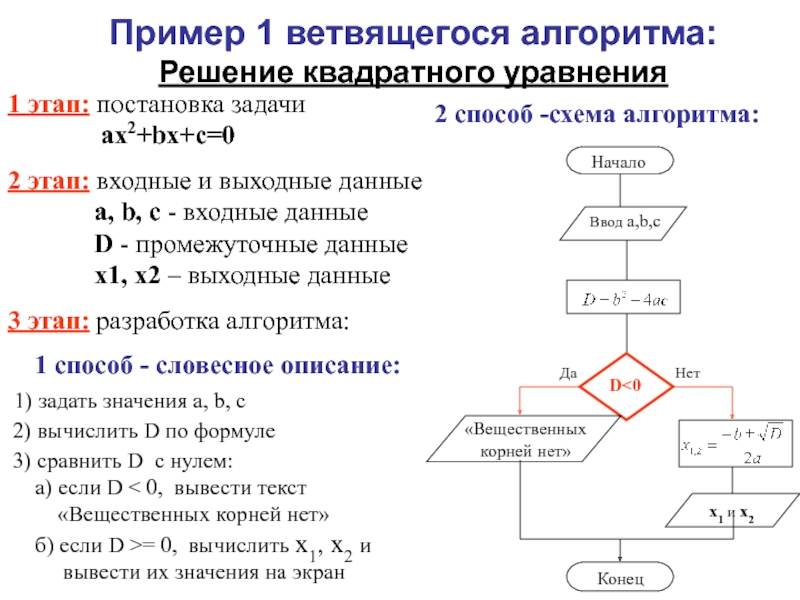
Слайд 10Пример 1 ветвящегося алгоритма:
Решение квадратного уравнения
1 этап: постановка задачи
аx2+bx+c=0
2 этап: входные и выходные
данные
a, b, c - входные данные
D - промежуточные данные
x1, x2 – выходные данные3 этап: разработка алгоритма:
1 способ - словесное описание:
1) задать значения a, b, c
2) вычислить D по формуле
3) сравнить D с нулем: а) если D < 0, вывести текст «Вещественных корней нет» б) если D >= 0, вычислить x1, x2 и вывести их значения на экран
2 способ -схема алгоритма:
Слайд 13Пример 3 ветвящегося алгоритма:
Организация меню (многовариантный выбор)
Составить схему алгоритма
следующей задачи:
1. На экран выводится окно с текстом меню:
Вычисление
площади кругаВычисление площади квадрата
Вычисление площади трапеции
Выход
Введите номер меню: _
2. С клавиатуры вводится номер меню.
3. В зависимости от введенного номера выполняется один из 4-х пунктов, причем после выполнения 1,2 или 3-го пунктов происходит возврат в окно меню.
Слайд 141 этап: постановка задачи -
формулы площадей:
2
этап: входные данные - R, a, b, h, n
выходные данные - S
Слайд 16Циклические алгоритмы
Организационно цикл состоит из следующих компонентов:
- подготовка цикла
- тело цикла
- условие продолжения цикла
Основные понятия:
- параметр
цикла
- начальное и конечное значение параметра цикла
- шаг циклаСлайд 17Пример 1 циклического алгоритма:
Вычисление таблицы значений функции
1 этап Постановка задачи:
Вычислить и вывести на экран таблицу значений X и Z,
где Z=X2 для 0,2 ≤ X ≤ 1,1 с шагом 0,32 этап Входные и выходные данные:
X - входные данные (1 ячейка ОЗУ)
Z - выходные данные (1 ячейка ОЗУ)
3 этап Разработка алгоритма
1 способ - словесное описание:
Вариант 1
1) X = 0.2
2) вычислить Z = X2
3) вывести X и Z
4) изменить X = X + 0.3
5) если X ≤ 1.1, то перейти к 2)
иначе перейти к п. 6)
6) конец
Вариант 2
1) X = 0.2
2) если X ≤1.1, то перейти к п. 3)
иначе перейти к п. 7)
3) вычислить Z = X2
4) вывести X и Z
5) изменить X = X + 0.3
6) перейти к п. 2)
7) конец
Слайд 183 типа циклических алгоритмов:
1. Цикл с постусловием
2. Цикл с предусловием
3.
Цикл со счетчиком
Слайд 191-й тип: Цикл с постусловием
2-й тип: Цикл с предусловием
Схемы циклических
алгоритмов 3-х типов
Здесь X – параметр цикла
…
…
Слайд 21Пример 2 циклического алгоритма
(без организации массива)
1 этап: постановка задачи
С клавиатуры
вводится последовательность чисел.
Найти сумму чисел до первого введенного «0».
2
этап: входные и выходные данные
A - входные данные (одна ячейка ОЗУ для ввода очередного числа)
S - выходные данные (одна ячейка ОЗУ для накопления суммы)3 этап: разработка алгоритма:
1) начальное значение S = 0
2) в циклической части происходит накопление S:
рекуррентная формула суммы: S = S + A
Замечание. Здесь заранее неизвестно, сколько раз выполнится цикл,
поэтому можно применить цикл с постусловием или цикл с
предусловием.
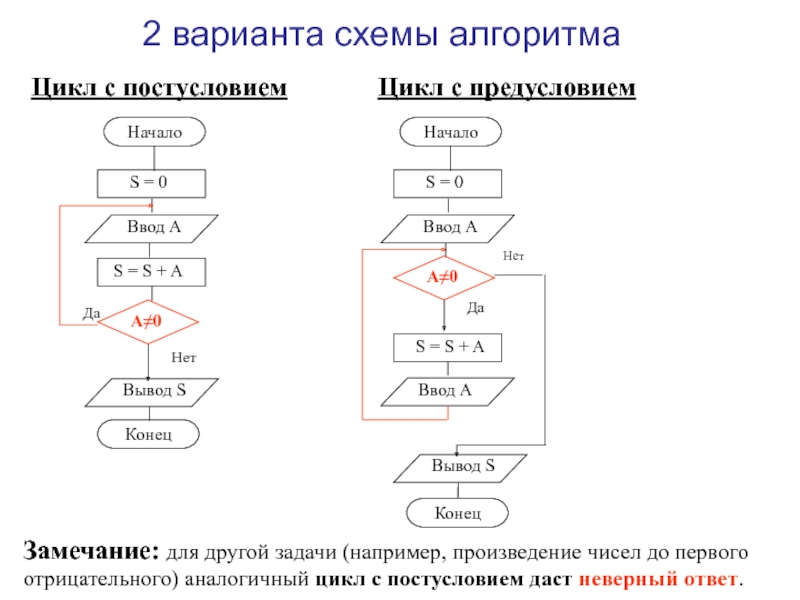
Слайд 22Цикл с постусловием
Цикл с предусловием
2 варианта схемы алгоритма
Замечание: для другой
задачи (например, произведение чисел до первого отрицательного) аналогичный цикл с
постусловием даст неверный ответ.Слайд 24Понятие массива
Массив – это конечная, упорядоченная последовательность элементов
одного типа, имеющая общее имя.
Элементы массива пронумерованы; обратиться к каждому
элементу можно, указав его индекс (номер)Количество индексов может быть разным (1, 2, 3,…), в зависимости от этого массивы могут быть одномерные и многомерные
Слайд 25Размер и размерность массива
Размер – это количество элементов
массива
Размерность (ранг) определяется
числом индексов элемента массива
(одномерные, двумерные,…)Слайд 26Обозначения 1-мерных массивов
Словесное описание:
Например, массив А
из 10 целых чисел;
массив R из 15 вещественных чиселМатематическое описание: - массив А: { Аi } i=1,10 или А(10) - элементы массива А: А1 А2 …Аi … А10
- массив R: { Ri } i=1,15 или R(15)
- элементы массива R: R1 R2 …Ri … R15
Замечание. 1. Размерность массивов А и R одинакова и равна 1.
2. Размер массивов разный ( 10 и 15 элементов)
Слайд 27Распределение ОЗУ (1-мерные массивы)
1. Массив А:
2. Массив R:
Номера ячеек:
1 2
3 … 15Имена ячеек:
R1 R2 R3 … R15
Слайд 28Стандартные алгоритмы для обработки одномерных массивов
Нахождение суммы всех элементов массива
(или части элементов)
Нахождение произведения всех элементов массива (или части элементов)
Подсчет
количества положительных и отрицательных элементов в массивеНахождение максимального и минимального элемента в массиве
Сортировка массива (расположение элементов в порядке возрастания или убывания их значений)
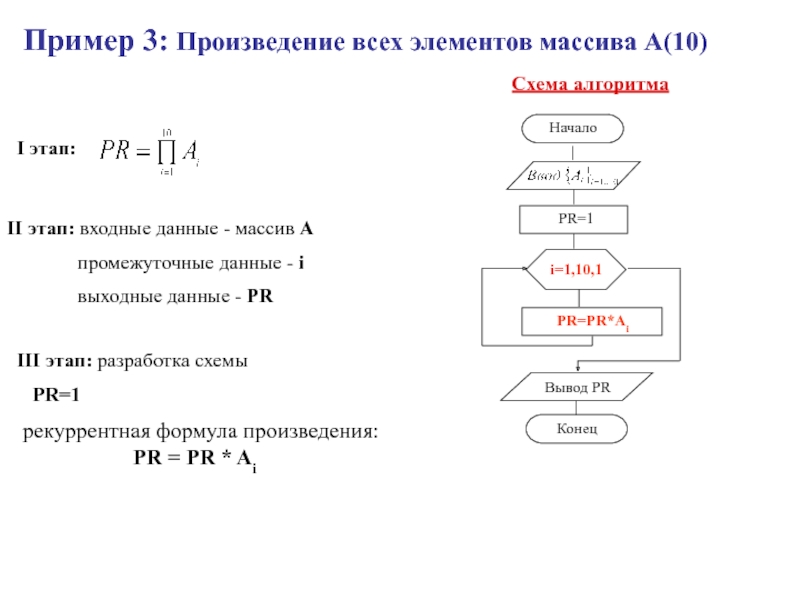
Слайд 31Пример 3: Произведение всех элементов массива А(10)
II этап: входные данные
- массив А
промежуточные
данные - iвыходные данные - PR
III этап: разработка схемы
PR=1
рекуррентная формула произведения:
PR = PR * Ai
Схема алгоритма
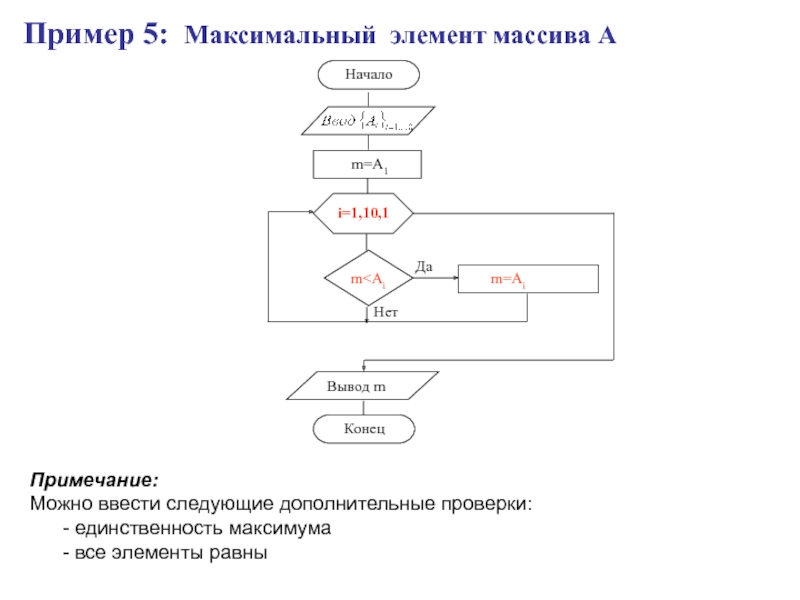
Слайд 33Пример 5: Максимальный элемент массива А
Примечание:
Можно ввести следующие дополнительные
проверки:
единственность максимума
все элементы равны
Слайд 35Алгоритм выбора
Исходный массив: 5 4 1 3 2
n=5
1 этап - находим макс. элемент и меняем местами с последним элементом: 2 4 1 3 5
2 этап – (рассматриваем массив на единицу короче n=4) находим макс. элемент и меняем местами с последним элементом в укороченном массиве: 2 3 1 4 5
3 этап – (рассматриваем массив на единицу короче n=3) находим макс. элемент и меняем местами с последним элементом в укороченном массиве 2 1 3 4 5
4 этап – (рассматриваем массив на единицу короче n=2) находим макс. элемент и меняем местами с последним элементом в укороченном массиве 1 2 3 4 5
5 этап – (рассматриваем массив на единицу короче n=1) находим макс. элемент и меняем местами с самим собой 1 2 3 4 5
Вывод: 1) на каждом этапе повторяются одни и те же действия
2) этапы отличаются только количеством элементов массива
3) число этапов равно размеру массива
Слайд 36Пример сложного цикла, где во внутреннем цикле ищется максимальный элемент
текущего фрагмента, а во внешнем цикле определяется количество этапов (n-1)
и происходит обмен максимального элемента и последнего элемента текущего фрагмента массиваСлайд 38Алгоритм обмена
Исходный массив: 5 4 1 3 2
n=5
1 этап – сравниваем два соседних элемента: если предыдущий больше последующего, то меняем их местами: 4 5 1 3 2 4 1 5 3 2 4 1 3 5 2 4 1 3 2 5
2 этап – (рассматриваем массив на единицу короче n=4) сравниваем два соседних элемента: если предыдущий больше последующего, то меняем их местами: 1 3 2 4 5
3 этап – (рассматриваем массив на единицу короче n=3) сравниваем два соседних элемента: если предыдущий больше последующего, то меняем их местами: 1 2 3 4 5
4 этап – (рассматриваем массив на единицу короче n=2) сравниваем два соседних элемента: если предыдущий больше последующего, то меняем их местами: 1 2 3 4 5
5 этап – (рассматриваем массив на единицу короче n=1) сравнения нет 1 2 3 4 5
Вывод: 1) на каждом этапе повторяются одни и те же действия
2) этапы отличаются только количеством элементов массива
3) число этапов равно размеру массива
Слайд 41Замечание. 1. Размерность массива А равна 2.
2. Размер
массива А - n х m элементовСловесное описание:
Например, матрица А(n,m) целых чисел
Математическое описание:
- матрица А: { Аij } i=1,n j=1,m или А(n х m)
- элементы матрицы А: А11 А12 А13 …А1m
А21 А22 А23 …А2m
А31 А32 А33 …А3m
. …
Аn1 Аn2 Аn3 …Аnm
Обозначения 2-мерных массивов
Слайд 42 Пример обозначения 2-мерных массивов
Замечание. 1. Размерность массива А равна
2.
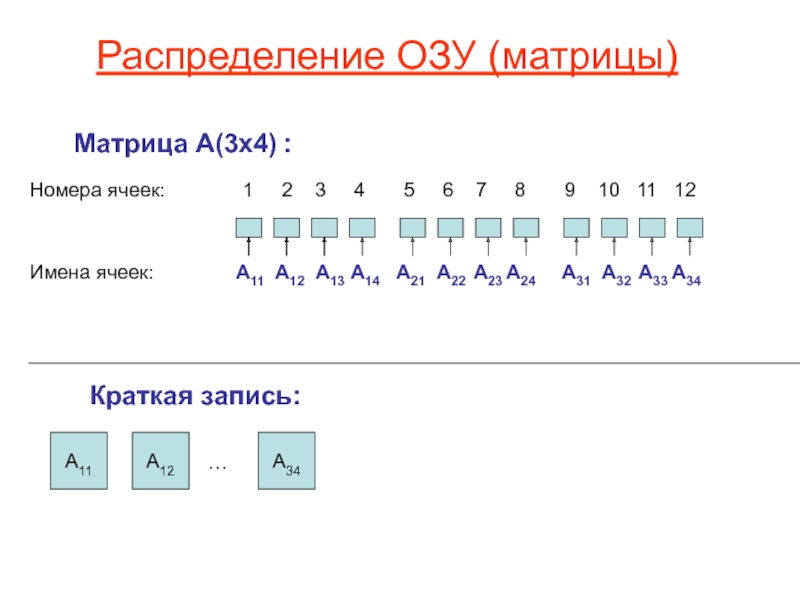
2. Размер массива А - 12 элементовСлайд 43Распределение ОЗУ (матрицы)
Матрица А(3х4) :
Номера ячеек:
1 2 3
4 5 6 7 8 9 10 11 12Имена ячеек:
А11 А12 А13 А14 А21 А22 А23 А24 А31 А32 А33 А34
Слайд 44Стандартные алгоритмы для обработки матриц
Вычисление суммы элементов матрицы
Вычисление произведения элементов
матрицы
Подсчет количества элементов, удовлетворяющих условию
Нахождение максимального и минимального элемента в
матрицеВычисление суммы (произведения, максимального, минимального и т.п.) в каждой строке или каждом столбце или в произвольной области матрицы
Формирование одномерного массива из элементов матрицы
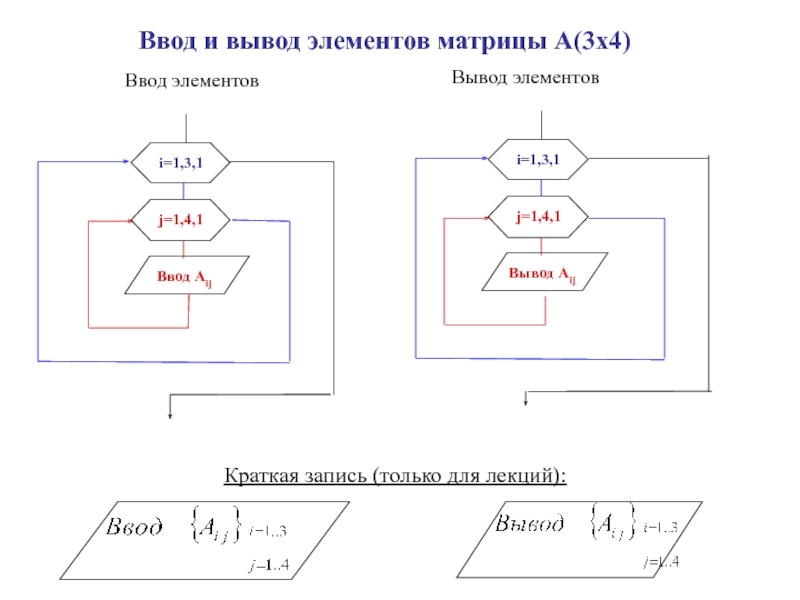
Слайд 45Ввод и вывод элементов матрицы А(3х4)
Вывод элементов
Ввод элементов
Краткая запись (только
для лекций):
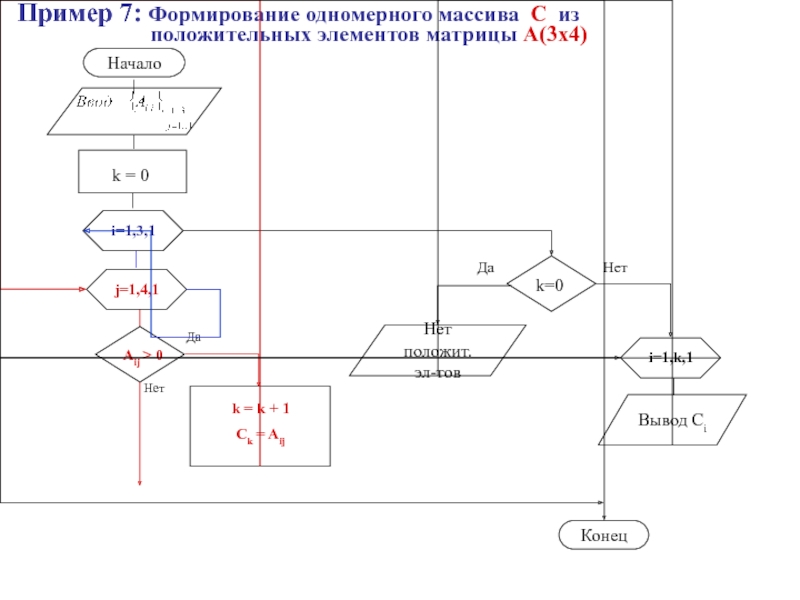
Слайд 52Пример 7: Формирование одномерного массива С из
положительных
элементов матрицы А(3х4)Нет положит.
эл-тов
Конец
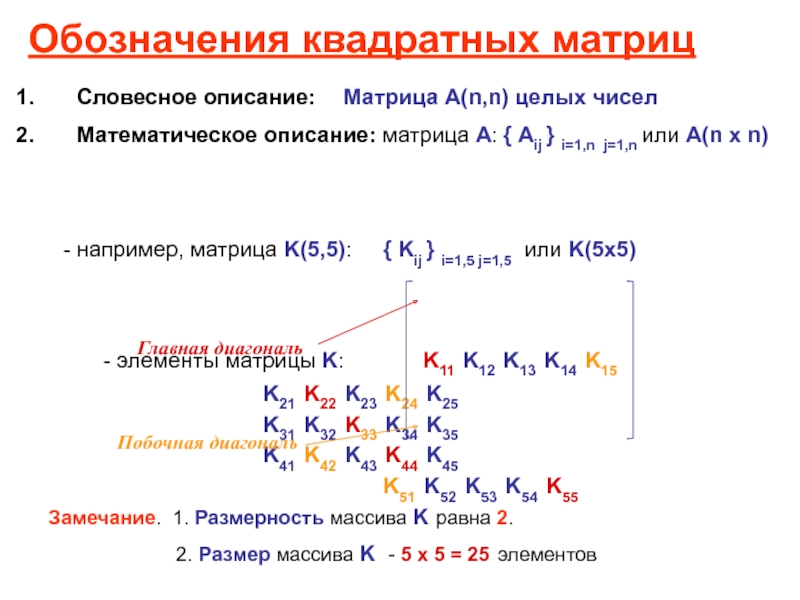
Слайд 55Замечание. 1. Размерность массива K равна 2.
2. Размер
массива K - 5 х 5 = 25 элементовСловесное описание: Матрица А(n,n) целых чисел
Математическое описание: матрица А: { Аij } i=1,n j=1,n или А(n х n)
- например, матрица K(5,5): { Kij } i=1,5 j=1,5 или K(5х5)
- элементы матрицы K: K11 K12 K13 K14 K15
K21 K22 K23 K24 K25
K31 K32 K33 K34 K35
K41 K42 K43 K44 K45
K51 K52 K53 K54 K55
Обозначения квадратных матриц
Слайд 56Стандартные алгоритмы для обработки квадратных матриц
Вычисление суммы, произведения, количества элементов
в указанной области, удовлетворяющих условию
Нахождение максимального и минимального элемента в
указанной области матрицыВычисление суммы (произведения, максимального, минимального и т.п.) в каждой строке или каждом столбце указанной области матрицы
Формирование одномерного массива из элементов указанной области матрицы
Слайд 58Определение областей
А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31
А32 А33 А34 А35
А41 А42 А43 А44 А45
А51 А52
А53 А54 А55А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31 А32 А33 А34 А35
А41 А42 А43 А44 А45
А51 А52 А53 А54 А55
А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31 А32 А33 А34 А35
А41 А42 А43 А44 А45
А51 А52 А53 А54 А55
А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31 А32 А33 А34 А35
А41 А42 А43 А44 А45
А51 А52 А53 А54 А55
i=1 j=1,2,3,4,5
i=2 j=2,3,4,5
i=3 j=3,4,5
i=4 j=4,5
i=5 j=5
i=1 j=1
i=2 j=1,2
i=3 j=1,2,3
i=4 j=1,2,3,4
i=5 j=1,2,3,4,5
1. Выше главной диагонали
2. Ниже главной диагонали
i=1 j=1,2,3,4,5
i=2 j=1,2,3,4
i=3 j=1,2,3
i=4 j=1,2
i=5 j=1
i=1 j=5
i=2 j=4,5
i=3 j=3,4,5
i=4 j=2,3,4,5
i=5 j=1,2,3,4,5
3. Выше побочной диагонали
4. Ниже побочной диагонали
A(5,5) i = 1, 5, 1
j = i, 5, 1
A(n,n) i = 1, n, 1
j = i, n, 1
A(5,5) i = 1, 5, 1
j = 1, i, 1
A(n,n) i = 1, n, 1
j = 1, i, 1
A(5,5) i = 1, 5, 1
j = 1, 6-i, 1
A(n,n) i = 1, n, 1
j = 1, n+1-i, 1
A(5,5) i = 1, 5, 1
j = 6-i, 5, 1
A(n,n) i = 1, n, 1
j = n+1-i, n, 1
Слайд 59А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31 А32
А33 А34 А35
А41 А42 А43 А44 А45
А51 А52 А53
А54 А55А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31 А32 А33 А34 А35
А41 А42 А43 А44 А45
А51 А52 А53 А54 А55
А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31 А32 А33 А34 А35
А41 А42 А43 А44 А45
А51 А52 А53 А54 А55
А11 А12 А13 А14 А15
А21 А22 А23 А24 А25
А31 А32 А33 А34 А35
А41 А42 А43 А44 А45
А51 А52 А53 А54 А55
5. Верхний треугольник
6. Нижний треугольник
7. Левый треугольник
8. Правый треугольник
i=1 j=1,2,3,4,5
i=2 j=2,3,4
i=3 j=3
j=1 i=1,2,3,4,5
j=2 i=2,3,4
j=3 i=3
i=3 j=3
i=4 j=2,3,4
i=5 j=1,2,3,4,5
j=3 i=3
j=4 i=2,3,4
j=5 i=1,2,3,4,5
A(5,5) i = 1, 3, 1
j = i, 6-i, 1
A(n,n) i = 1, n/2, 1
j = i, n+1-i, 1
A(5,5) i = 3, 5, 1
j = 6-i, i, 1
A(n,n) i = n/2, n, 1
j = n+1-i, i, 1
A(5,5) j = 1, 3, 1
i = j, 6-j, 1
A(n,n) j = 1, n/2, 1
i = j, n+1-j, 1
A(5,5) j = 3, 5, 1
i = 6-j, j, 1
A(n,n) j = n/2, n, 1
i = n+1-j, j, 1
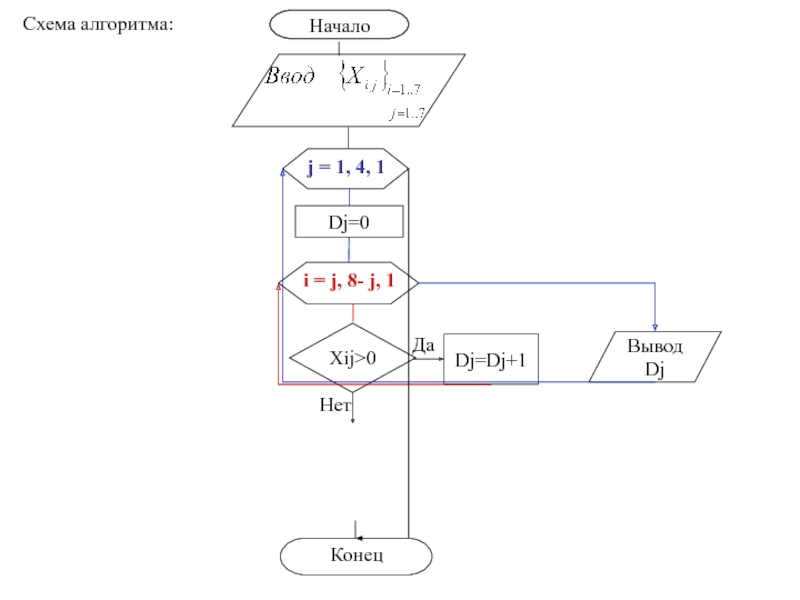
Слайд 63Пример 4: Сформировать одномерный массив D из количеств положительных элементов
каждого столбца в заштрихованной области матрицы X(7,7)
III этап: Словесное описание
Просматривать
по столбцам элементы заштрихованной области. В начале просмотра столбца присвоить Dj=0. Если рассматриваемый элемент Xij положительный, то увеличить Dj на 1.X11 X12 X13 X14 X15 X16 X17
X21 X22 X23 X24 X25 X26 X27
X31 X32 X33 X34 X35 X36 X37
X41 X42 X43 X44 X45 X46 X47
X51 X52 X53 X54 X55 X56 X57
X61 X62 X63 X64 X65 X66 X67
X71 X72 X73 X74 X75 X76 X77
Слайд 66Пример
Дано:
Схема алгоритма
Входной поток данных:
8 -4 -1 3 -2 1
-1 5 6
Задача:
Сформулировать постановку задачи
Нарисовать все состояния ячеек ОЗУ
Определить значения
выходных данныхСлайд 68Подход к решению
Определить тип задачи (сумма, произведение, количество, max, min,
ветвление и т.п.):
Что выводится (выходные данные)?
Какие начальные значения?
Как вычисляются выходные
данные?Выписать все переменные, задействованные в задаче; нарисовать ячейки ОЗУ
Определить состояния ячеек ОЗУ (ввод данных, каждый шаг каждого цикла вычислений, вывод данных)
Записать значения выходных данных
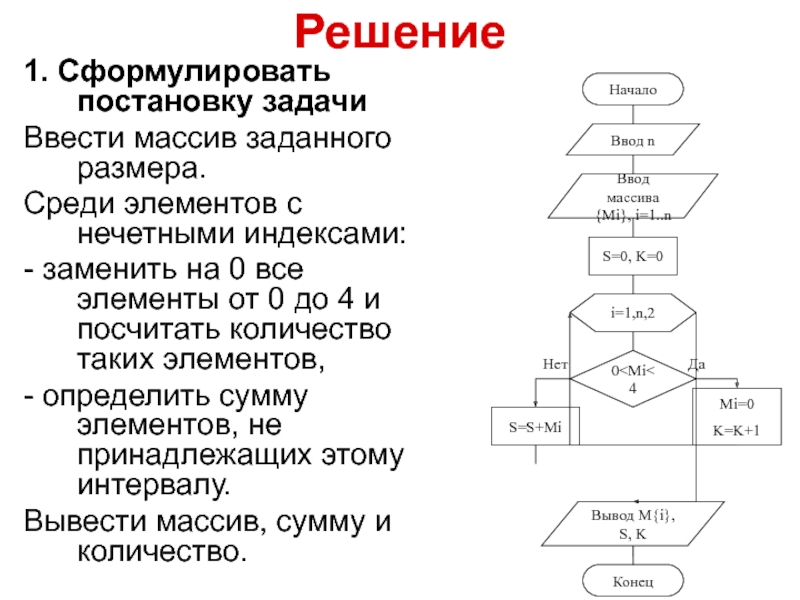
Слайд 69Решение
1. Сформулировать постановку задачи
Ввести массив заданного размера.
Среди элементов с нечетными
индексами:
- заменить на 0 все элементы от 0 до 4
и посчитать количество таких элементов,- определить сумму элементов, не принадлежащих этому интервалу.
Вывести массив, сумму и количество.
Ввод n
Ввод массива {Mi}, i=1..n
S=0, K=0
i=1,n,2
0 S=S+Mi Mi=0 Вывод M{i}, S, K Начало Конец Да Нет
K=K+1
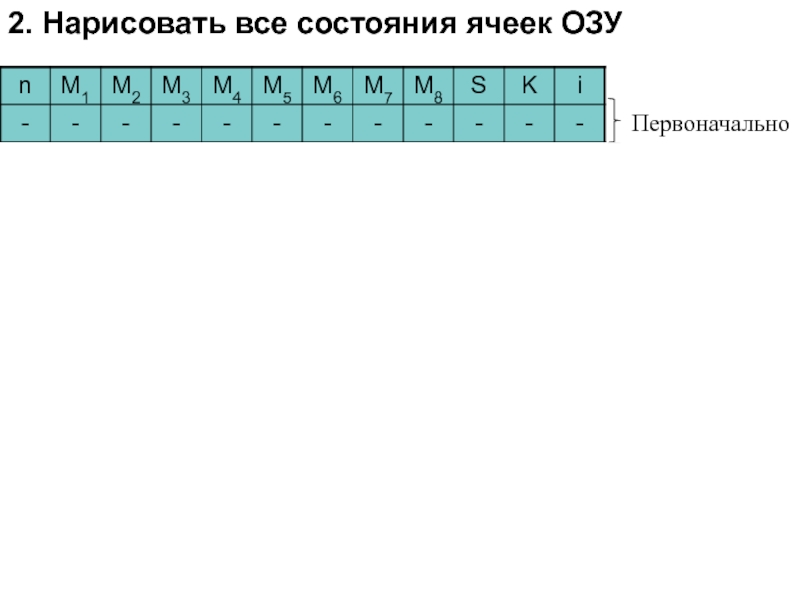
Слайд 702. Нарисовать все состояния ячеек ОЗУ
Первоначально
Ввод массива
Начальные значения
переменных S
и K
Слайд 71
Было перед
основным
циклом
Основной
цикл
Цикл для
вывода
массива,
вывод S и
K
2. (продолжение)
Не пишем!
После вывода
Примечание:
В зависимости от среды и языковой конструкции,
используемой при программировании алгоритма, возможны следующие значения переменной i после выполнения цикла:i=8 (конечное значение в цикле)
i не определено (и др.)