Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОНЯТИЕ ЛОГАРИФМА
Содержание
- 1. ПОНЯТИЕ ЛОГАРИФМА
- 2. Для чего были придуманы логарифмы? Кто является
- 3. Джон Непер«Я старался, насколько мог и умел,
- 4. Определение логарифмаЛогарифмом числа в>0 по основанию а,
- 5. Запомни
- 6. Вычислить:
- 7. Основное логарифмическое тождествоНапример,
- 8. Свойства логарифмовЛогарифм произведения положительных чисел равен сумме логарифмов сомножителей:
- 9. Свойства логарифмовЛогарифм частного положительных чисел равен разности логарифмов делимого и делителя:
- 10. Свойства логарифмовЛогарифм степени положительного основания равен произведению показателя степени на логарифм основания степени:
- 11. Свойства монотонности логарифмовЕсли a>1 и Сравнить:
- 12. Свойства монотонности логарифмовЕсли 0 < а
- 13. Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию
- 14. Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию
- 15. Десятичные логарифмыЕсли основание логарифма равно 10, то логарифм называется десятичным:
- 16. Десятичные логарифмы чисел, выраженных единицей с последующими нулями:
- 17. Десятичные логарифмы чисел, выраженных единицей с предшествующими нулями
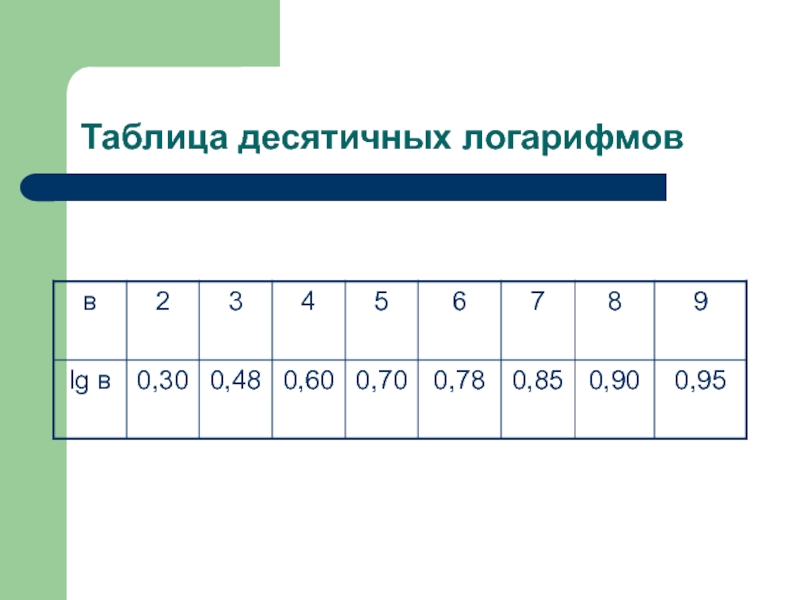
- 18. Таблица десятичных логарифмов
- 19. Натуральные логарифмыЕсли основание логарифма е 2,7, то логарифм называется натуральным:
- 20. Натуральные логарифмы
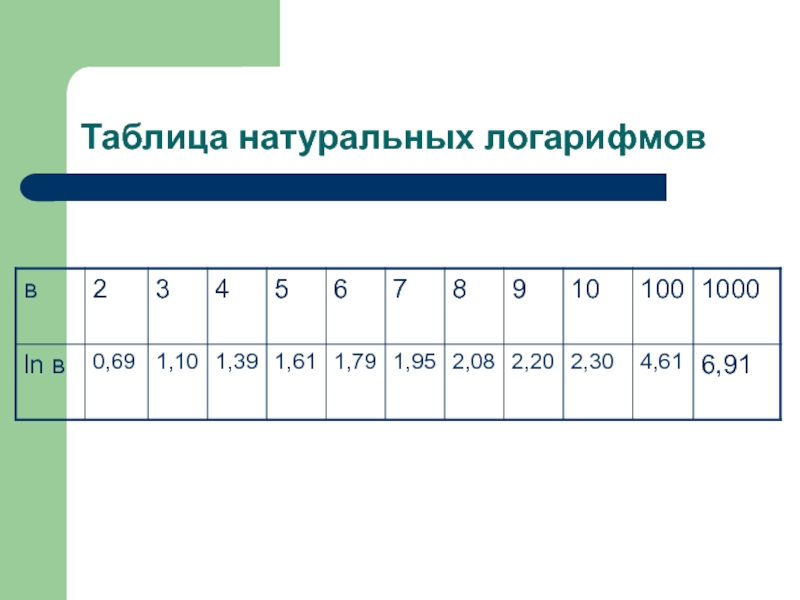
- 21. Таблица натуральных логарифмов
- 22. Логарифмирование алгебраических выраженийЕсли число х представлено
- 23. Прологарифмировать алгебраическое выражение:Пример:
- 24. Потенцирование логарифмических выраженийПереход от логарифмического выражения
- 25. Перейти к алгебраическому выражению
- 26. Скачать презентанцию
Для чего были придуманы логарифмы? Кто является изобретателем логарифмов?Конечно же, для ускорения и упрощения вычислений. Изобретатель первых логарифмических таблиц шотландский математик Джон Непер
Слайды и текст этой презентации
Слайд 2Для чего были придуманы логарифмы? Кто является изобретателем логарифмов?
Конечно же,
для ускорения и упрощения вычислений.
Изобретатель первых логарифмических таблиц шотландский
математикДжон Непер
Слайд 3Джон Непер
«Я старался, насколько мог и умел, отделаться от трудности
и скуки вычислений, докучность которых отпугивает весьма многих от изучения
математики»
Слайд 4Определение логарифма
Логарифмом числа в>0 по основанию а, где а>0 и
а 1, называется показатель степени х, в которую
нужно возвести число а, чтобы получить число в.
Слайд 8Свойства логарифмов
Логарифм произведения положительных чисел равен сумме логарифмов сомножителей:
Слайд 9Свойства логарифмов
Логарифм частного положительных чисел равен разности логарифмов делимого и
делителя:
Слайд 10Свойства логарифмов
Логарифм степени положительного основания равен произведению показателя степени на
логарифм основания степени:
Слайд 22Логарифмирование
алгебраических выражений
Если число х представлено алгебраическим выражением, то логарифм
любого выражения можно выразить через логарифмы составляющих его чисел.
(на основании
свойств логарифмов)
Слайд 24Потенцирование
логарифмических выражений
Переход от логарифмического выражения к алгебраическому называется потенцированием,
то есть, произвести действие, обратное логарифмированию
