Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие об алгоритме. Свойства алгоритмов. Способы записи алгоритмов
Содержание
- 1. Понятие об алгоритме. Свойства алгоритмов. Способы записи алгоритмов
- 2. Оглавление:Основные этапы решения задач на компьютере.Понятие алгоритма. Свойства алгоритма.Форма представления алгоритмаСтруктурные схемы алгоритмоввпередназад
- 3. Основные этапы решения задач на компьютере:Этот процесс
- 4. Понятие алгоритма. Свойства алгоритма.Алгоритм это точное предписание,которое
- 5. Форма представления алгоритмаФорма представления алгоритма может быть
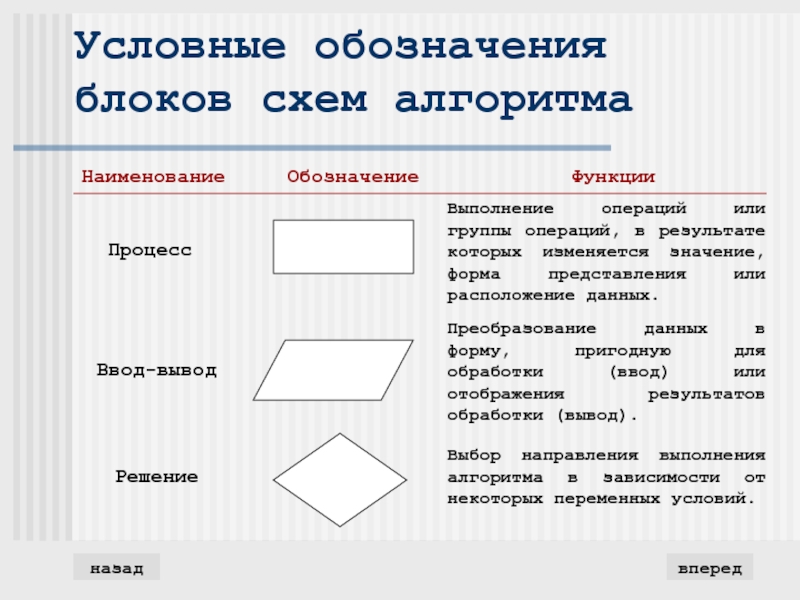
- 6. Условные обозначения блоков схем алгоритмавпередназад
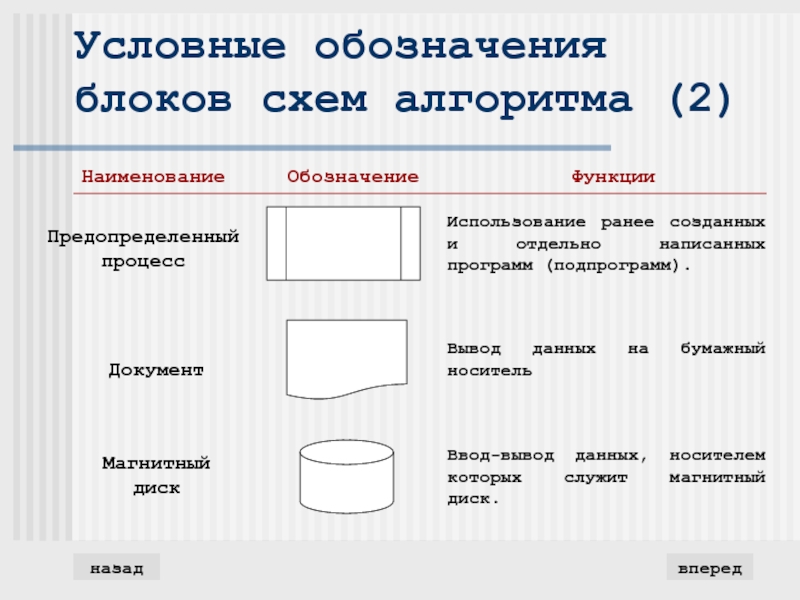
- 7. Условные обозначения блоков схем алгоритма (2)впередназад
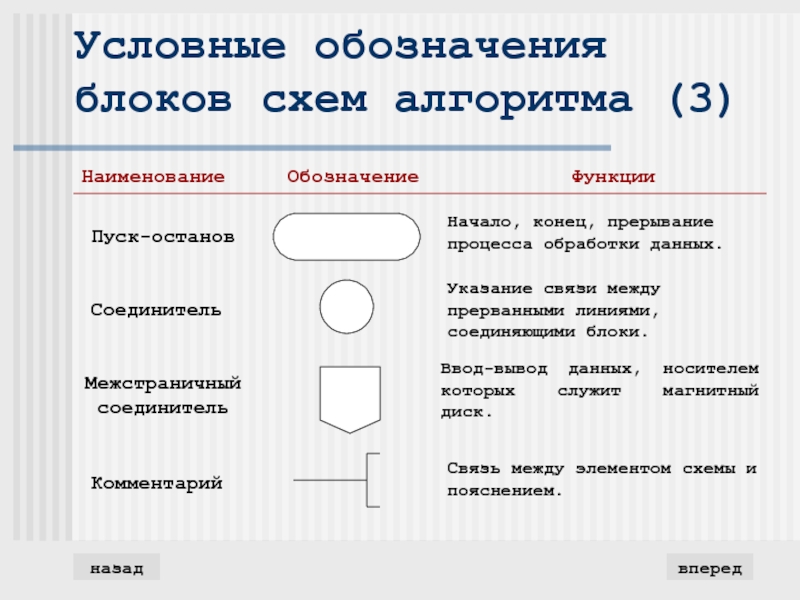
- 8. Условные обозначения блоков схем алгоритма (3)впередназад
- 9. Пример 1. Решение квадратного уравненияИсходные данные:Значения
- 10. Структурные схемы алгоритмовОдним из свойств алгоритма является
- 11. Линейные алгоритмыЛинейным принято называть процесс, в котором
- 12. Ветвящиеся алгоритмыВетвящимися называется процесс, если для его
- 13. Циклические алгоритмыЦиклическими называются программы, содержащие циклы. Цикл
- 14. Циклические алгоритмы Пример нахождения суммы 10-ти чиселвпередназад
- 15. Контрольные вопросы:Назовите этапы подготовки и решения задач
- 16. Литература:В.Б.Попов, Turbo-Pascal для школьников, стр.15-19,А.Д.Хомоненко, Основы современных
- 17. Решение задач включает следующие основные этапы, часть
- 18. 6. Отладка:анализ результатов тестирования;устранение ошибок, совершенствование программы.
- 19. Тест=совокупность данныхдля программыточное описание предполагаемыхрезультатов+
- 20. Слайд 20
- 21. Отсутствие сообщений редактора данной среды программированияо синтаксических
- 22. Примеры ошибок в циклах: неверное условие
- 23. Примеры ошибок в арифметических операциях: неверное
- 24. Выбор методов решения задач Чтобы
- 25. Слайд 25
- 26. Примеры рекуррентных соотношений: нахождение членов арифметических
- 27. Легко заметить закономерность: член ряда равен сумме
- 28. Даже сам человек создан по закону «золотого
- 29. Великий итальянский ученый Фебоначчи
- 30. Астрономия до Евдокса не знала сфер. Платон говорит о «кругах», Аристотель о «небесных светилах»,
- 31. В небесной «гармонии» 8 разновысотных звуков: звёздное небо (высший
- 32. В то время как средневековые философы использовали
- 33. Иоганн Кеплер
- 34. Иоганн Кеплер«Геометрия имеет два великих сокровища; Одно
- 35. Слайд 35
- 36. Слайд 36
- 37. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Оглавление:
Основные этапы решения задач на компьютере.
Понятие алгоритма. Свойства алгоритма.
Форма представления
алгоритма
Слайд 3Основные этапы решения задач на компьютере:
Этот процесс можно представить в
виде
нескольких последовательных этапов:
Постановка задачи,
Математическое или информационное моделирование,
Алгоритмизация задачи,
Программирование,
Ввод программы
и исходных данных в ЭВМ,Тестирование и отладка программ,
Исполнение отлаженной программы и анализ результатов.
вперед
назад
Слайд 4Понятие алгоритма. Свойства алгоритма.
Алгоритм это точное предписание,которое определяет процесс, ведущий
от исходных данных к требуемому конечному результату. Алгоритм должен быть
понятен исполнителю(компьютеру, роботу и пр.)Любой применимый алгоритм обладает следующими основными свойствами:
Результативностью
Определенностью
Массовостью.
Результативность означает возможность получения результата после выполнения конечного количества операций. Определенность состоит в совпадении получаемых результатов независимо от пользователя и применяемых технических средств. Массовость заключается в возможности применения алгоритма к целому классу однотипных задач.
вперед
назад
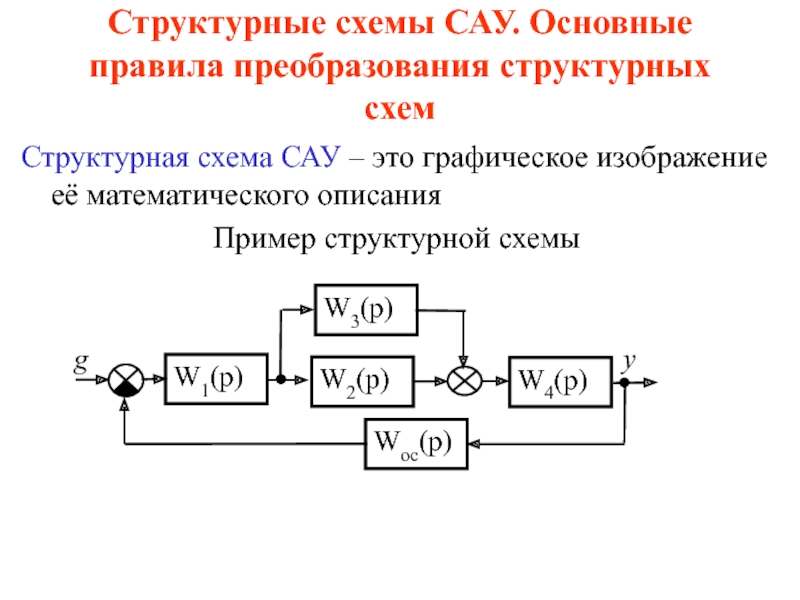
Слайд 5Форма представления алгоритма
Форма представления алгоритма может быть разной: словесно-формульная,структурная –
блок-схема,граф-схема и др.
Блок-схемный алгоритм изображается геометрическими фигурами (блоками), связанными по
управлению линиями (направлениями потока)со стрелками. В блоках записывается последовательность действий. Блок-схема дает более наглядное представление алгоритма: каждая операция представлена отдельной геометрической фигурой. Кроме того графическое изображение наглядно показывает разветвление путей решения задачи в зависимости от различных условий, повторение отдельных этапов процесса и другие детали.
вперед
назад
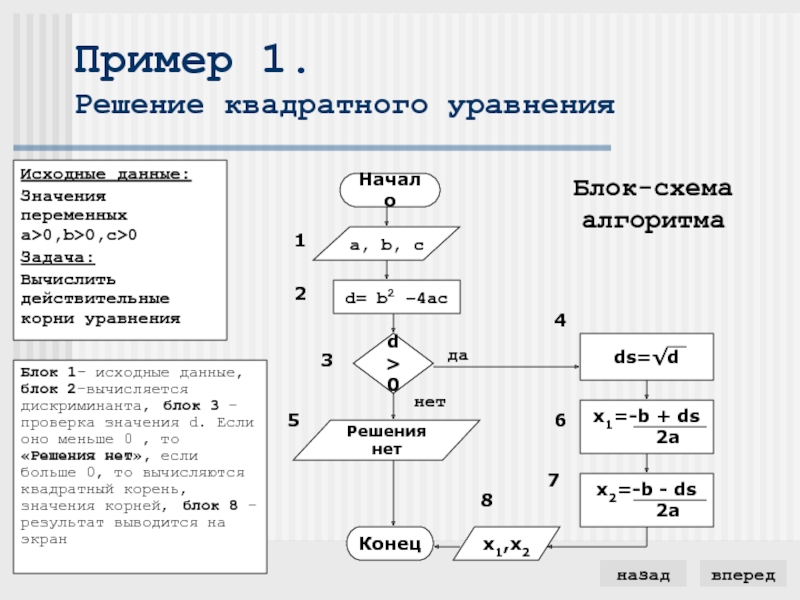
Слайд 9Пример 1.
Решение квадратного уравнения
Исходные данные:
Значения переменных a>0,b>0,c>0
Задача:
Вычислить действительные корни
уравнения
a, b, c
d= b2 –4ac
d>0
ds=d
x1=-b + ds
2ax2=-b - ds
2a
Решения нет
x1,x2
Конец
Начало
1
2
3
4
5
6
7
8
да
нет
Блок 1- исходные данные,блок 2–вычисляется дискриминанта, блок 3 – проверка значения d. Если оно меньше 0 , то «Решения нет», если больше 0, то вычисляются квадратный корень,значения корней, блок 8 – результат выводится на экран
Блок-схема алгоритма
вперед
назад
Слайд 10Структурные схемы алгоритмов
Одним из свойств алгоритма является дискретность – возможность
расчленения процесса вычислений, предписанных алгоритмом, на отдельные этапы, возможность деления
участков программы с определенной структурой. Можно выделить и наглядно представить графически три простейшие структуры:Последовательность двух или более операций,
Выбор направления,
Повторение.
Любой вычислительный процесс может быть представлен как комбинация этих элементарных алгоритмических структур. Соответственно, вычислительные процессы, выполняемые на ЭВМ по заданной программе, можно разделить на три основных вида:
Линейные
Ветвящиеся
Циклические
вперед
назад
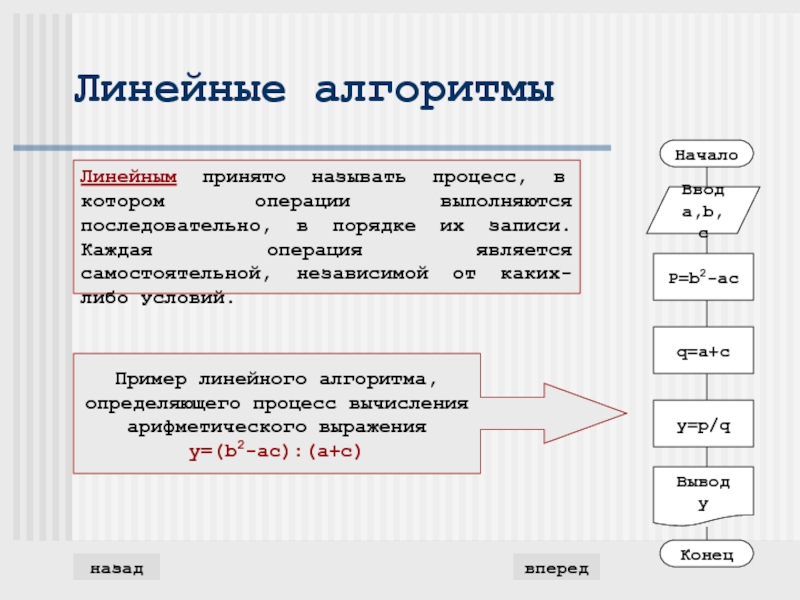
Слайд 11Линейные алгоритмы
Линейным принято называть процесс, в котором операции выполняются последовательно,
в порядке их записи. Каждая операция является самостоятельной, независимой от
каких-либо условий.Пример линейного алгоритма,
определяющего процесс вычисления
арифметического выражения
y=(b2-ac):(a+c)
вперед
назад
Слайд 12Ветвящиеся алгоритмы
Ветвящимися называется процесс, если для его реализации предусмотрено несколько
направлений (ветвей). Каждое отдельное направление является отдельной ветвью вычислений. Направление
ветвления выбирается логической проверкой, в результате которой возможно два ответа: «да» - условие выполнено, «нет» - условие не выполнено.да
вперед
назад
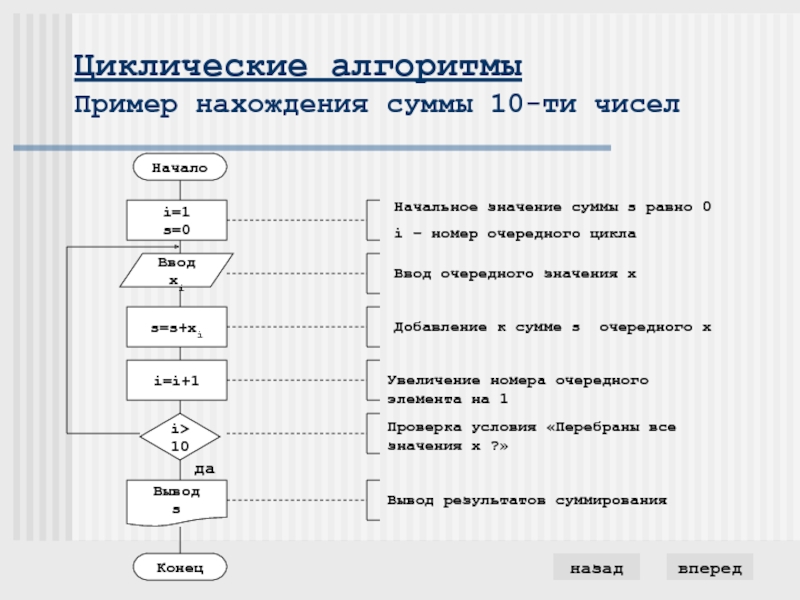
Слайд 13Циклические алгоритмы
Циклическими называются программы, содержащие циклы. Цикл – это многократно
повторяемый участок программы.
В организации цикла можно выделить следующие этапы:
Подготовка цикла,
Выполнение
вычислений цикла (тело цикла),Модификация параметров,
Проверка условий окончания цикла.
Цикл называется детерминированным, если число повторений тела цикла заранее известно или определено. Цикл называется итерационным, если число повторений заранее неизвестно, а зависит от значений параметров, участвующих в вычислениях.
вперед
назад
Слайд 15Контрольные вопросы:
Назовите этапы подготовки и решения задач на ЭВМ.
Что такое
алгоритм и какими свойствами он обладает?
Укажите формы представления алгоритмов.
Опишите структурные
схемы алгоритмов.Составьте и запишите алгоритмы (в тетради):
Даны две простые дроби.Составить алгоритм получения дроби, являющейся результатом их деления.
Написать алгоритм вычисления по формуле:
y=(1-x2+2,5x3+x4)2,учитывая следующие ограничения:
Пользоваться можно только операциями сложения, вычитания и умножения; каждое выражение может содержать только одну арифметическую операцию.
Внимание!Выражение – запись, определяющая последовательность действий над величинами. Выражение может содержать константы, переменные, знаки операций, функции.
вперед
назад
Слайд 16Литература:
В.Б.Попов, Turbo-Pascal для школьников, стр.15-19,
А.Д.Хомоненко, Основы современных компьютерных технологий, стр.36-46,
Задачник-практикум
под ред. И.Семакина, стр.204-208,
Ю.Шафрин, Информационные технологии, стр.43-52.
возврат
Слайд 17
Решение задач включает следующие основные этапы, часть из которых осуществляется
без участия ЭВМ.
1. Постановка задач:
сбор информации о задаче;
формулировка условия
задачи;определение конечных целей;
описание данных.
2. Построение математической модели.
3. Построение алгоритма:
выбор формы записи алгоритма (блок-схема, табличная и др.);
запись алгоритма.
4. Программирование:
выбор языка программирования;
выбор способа представления данных;
запись алгоритма на выбранном языке;
выбор тестов и методов тестирования.
5. Тестирование:
проверка работоспособности программы.
Слайд 186. Отладка:
анализ результатов тестирования;
устранение ошибок, совершенствование программы.
7. Сопровождение
программы:
доработка программы для решения конкретных задач;
составление документации к использованию.
Тестирование устанавливает
факт наличия ошибки.Отладка выясняет её причину.
Программа-отладчик обеспечивает следующие возможности:
пошаговое исполнение программы с остановкой после каждого оператора;
просмотр в процессе отладки текущего значения любой переменной или
нахождение значения любого выражения;
установку в программе контрольных точек, в которых программа временно
прекращает своё выполнение, так что можно оценить промежуточные
результаты.
При отладке важно помнить:
лучше использовать простые тестовые данные;
ошибки разделять и устранять поочерёдно,
не вносить в программу сразу несколько изменений;
не следует считать причиной ошибок транслятор .
!
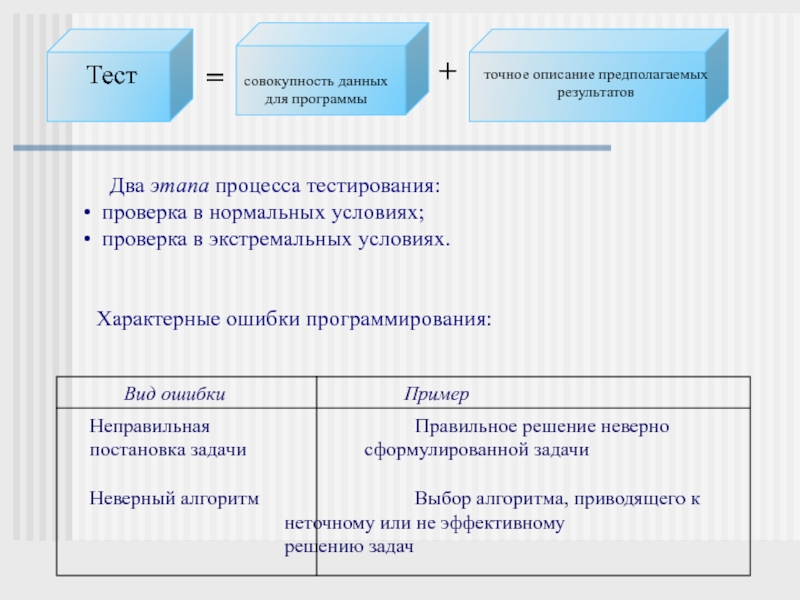
Слайд 19Тест
=
совокупность данных
для программы
точное описание предполагаемых
результатов
+
Два этапа процесса тестирования:
проверка в нормальных условиях; проверка в экстремальных условиях.
Характерные ошибки программирования:
Вид ошибки Пример
Неправильная Правильное решение неверно
постановка задачи сформулированной задачи
Неверный алгоритм Выбор алгоритма, приводящего к
неточному или не эффективному
решению задач
Слайд 21 Отсутствие сообщений редактора данной среды программирования
о синтаксических ошибках является необходимым
, но недостаточным
условием, чтобы считать программу правильной.
!
Примеры синтаксических ошибок:
неправильная запись формата оператора; несогласованность скобок;
пропуск разделителей.
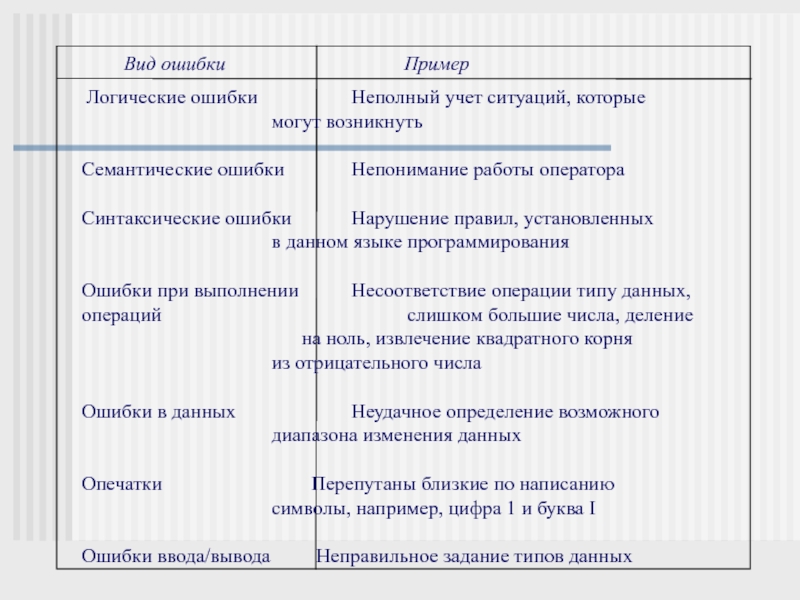
Примеры логических ошибок:
неверное указание ветви алгоритма после проверки некоторого
условия;
неполный учет возможных условий;
пропуск в программе одного или более блоков алгоритма.
Слайд 22Примеры ошибок в циклах:
неверное условие выполнения или окончания
цикла;
неверное задание счётчика цикла;
бесконечный цикл.
Примеры ошибок
ввода/вывода и ошибок при работе с данными:неправильное задание типа данных;
организация считывания меньшего или большего объема
данных, чем требуется.
Примеры ошибок в использовании переменных:
повторное использование имени переменной для обозначения другой
величины;
ошибочное использование одной переменной вместо другой.
Примеры ошибок при работе с массивами:
неправильно задан размер массива;
неправильно задан тип массива.
Слайд 23Примеры ошибок в арифметических операциях:
неверное указание типа переменной
(например, целого вместо
вещественного);
неверное определение порядка
действий;деление на нуль;
извлечение квадратного корня из отрицательного числа;
Эти ошибки обнаруживаются с помощью тестирования.
Программа, предназначенная для длительной эксплуатации,
должна иметь соответствующую документацию и инструкцию по
ее использованию (т.н. Help).
!
Слайд 24 Выбор методов решения задач
Чтобы решить задачу необходима
точная постановка задачи и правильный выбор метода решения задачи. Постановка
задачи сводится, как правило, к математической форме описания условий задачи по схеме:Задача (словесное описание).
Дано (перечисление исходного).
Требуется (перечисление требуемого).
Связь (зависимость между исходным и требуемым).
При (условия допустимости исходного).
Выбор метода решения должен обеспечить получение требуемых результатов для любых допустимых исходных данных.
Методы решения задач:
рекуррентный;
рекурсивный;
приближённые методы.
Слайд 25
Рекуррентный метод
Метод, использующий
рекуррентные соотношения, называется рекуррентным.Формулы, в которых очередной член последовательности выражается через один или несколько предыдущих членов, называются рекуррентными соотношениями.
В программировании часто используют метод рекуррентного суммирования для определения суммы конечной последовательности чисел.
Применим ранее описанную схему:
Задача (найти сумму конечной последовательности заданных чисел).
Дано (x1, x2…xn – последовательность n чисел).
Требуется (найти S – сумму этих чисел).
Связь (S = x1+ x2+…+xn ).
При (любых значениях чисел последовательности).
Применив рекуррентный метод, получим соотношения:
S0 = 0
Sk = Sk – 1 + xk k =1,2,…n
S = Sn
Слайд 26 Примеры рекуррентных соотношений:
нахождение членов арифметических и геометрических
прогрессий;
нахождение членов ряда Фибоначчи.
Итальянский математик XVI
в. Фибоначчи построил математический ряд 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,…, описывающий биологический процесс (процесс размножения кроликов). Попробуйте записать рекуррентное соотношение для этого ряда.Слайд 27
Легко заметить закономерность: член ряда равен сумме двух предыдущих членов.
Если в таком ряду взять отношение последующего члена к предыдущему
и наоборот, получим числа 1,618 и 0,618. Эти числа были открыты «пифагорейцами» и получили название «золотых».Они являются корнями квадратного уравнения, которое можно вывести из следующей пропорции:
A+B = A A B
A B
A и B – соответственно две части одного отрезка.
Числа эти не зря названы «золотыми». «Пифагорейцы» же заметили, что музыкальный звукоряд построен по закону соотношений частот, равных «золотому» числу. И везде, где человек ощущает гармонию: в звуках, живописи, размерах – всюду присутствуют «золотые» числа (числа Фибоначчи).
К изумлению Кеплера, создававшего свою модель солнечной системы и уже знавшего основные размеры планет, периоды их обращения и взаимные расстояния, эти числа оказались числами Фибоначчи. Оказалось, что весь ближний космос организован по законам музыкальной гармонии. (Всё это Кеплер изложил в своей книге «Музыка сфер».)
.
Слайд 28
Даже сам человек создан по закону «золотого сечения». Так, дельта-ритмы
мозга при реакции на внешний раздражитель – это затухающие апериодические
колебания, соседние периоды которых относятся по закону «золотого сечения».Если рост человека принять за весь отрезок, а пупок – точка деления, то от него вниз – часть А, а вверх часть – В. Для мужчин это соотношение в среднем 1,7, а для женщин 1,5, т.е. мужчины в среднем стройнее (не из интуитивного ли стремления соответствовать гармонии «золотого сечения» появились туфли на каблуках?).
В ряду Фибоначчи чем больше порядковый номер членов ряда, тем точнее выполняется «золотое соотношение». Проверьте это.
Слайд 30Астрономия до Евдокса не знала сфер. Платон говорит о «кругах», Аристотель о «небесных светилах», или «звёздах». В
латинской науке поздней античности и средневековья то же понятие передаётся
чаще всего как «небесная гармония», «небесная музыка», «мировая гармония»Слайд 31В небесной «гармонии» 8 разновысотных звуков: звёздное небо (высший тон), Сатурн, Юпитер,
Марс, Меркурий, Венера, Солнце, Луна (низший тон).
Слайд 32В то время как средневековые философы использовали понятие «музыка сфер»
лишь метафорически, Кеплер рассчитал математические соотношения в движении планет и увязал их
с музыкальными интервалами, установив семь основных гармонических интервалов (консонансов): октаву (2/1), большую сексту (5/3), малую сексту (8/5), ...Слайд 34Иоганн Кеплер
«Геометрия имеет два великих сокровища; Одно — это теорема
Пифагора; Другое — разделение линии на экстремальное и среднее соотношение.
Первое
можно сравнить с мерой золота; Второе мы можем назвать драгоценным камнем».Слайд 35
Рекурсивный
методРекурсивным называется метод вычисления функций через самих себя.
Иногда значение функции для некоторых аргументов можно выразить через значение этой же функции от других аргументов.
Пример 1:
sin(x+ ) = – sin(x) для всех вещественных x.
Пример 2:
1, если n = 1;
n! =
(n-1)! n, если n > 1.
Слайд 36
Метод Монте-Карло (приближённый метод)
Метод используется для вычисления площади фигуры, ограниченной произвольным контуром.Пусть есть фигура на плоскости, и пусть она расположена внутри квадрата, сторона которого, А, известна. Площадь фигуры можно вычислить, засыпав
квадрат слоем песка. Число песчинок внутри
квадрата будет пропорционально его площади, а число
песчинок внутри фигуры – пропорционально её площади.
Из этой пропорции можно определить площадь фигуры.
Эта задача легко моделируется и программируется. Роль песчинок могут играть точки выводимые произвольно на заданный участок. Их координаты
можно задавать с помощью генератора случайных чисел.
А
А
Y
X
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.