Слайд 1Понятие площади многоугольника
Слайд 2Понятие площади
В жизни часто приходится вычислять площади геометрических фигур.
Например, приходится
определять площадь поля, огорода, спортивной площадки или определять площадь пола
в здании, площадь стен или окон в комнате.
При всяком измерении необходимо заранее иметь меру, с которой сравнивается измеряемая величина. При взвешивании употребляются меры веса: килограмм, грамм, тонна, центнер. Время измеряется часами, минутами, секундами.
При измерении длины отрезка МN сравниваем его с метром, сантиметром или с какой-нибудь другой мерой длины. При измерении углов пользуемся угловыми градусами, минутами.
Точно так же при измерении площадей геометрических фигур пользуются особыми мерами, с которыми сравниваются эти фигуры.
Слайд 4Единицы измерения площадей
Такими мерами являются квадраты, стороны которых равны какой-нибудь
линейной мере: метру, дециметру, сантиметру, миллиметру.
При измерении площадей, имеющих
большие размеры, за меру может быть принят квадрат, сторона которого равна километру.
Квадрат, сторона которого равна какой-нибудь линейной единице, называется квадратной единицей: квадратным метром, квадратным сантиметром, квадратным километром и т. д.,
Измерить площадь какой-нибудь геометрической фигуры — значит узнать, сколько тех или иных квадратных единиц содержится в фигуре, площадь которой измеряется.
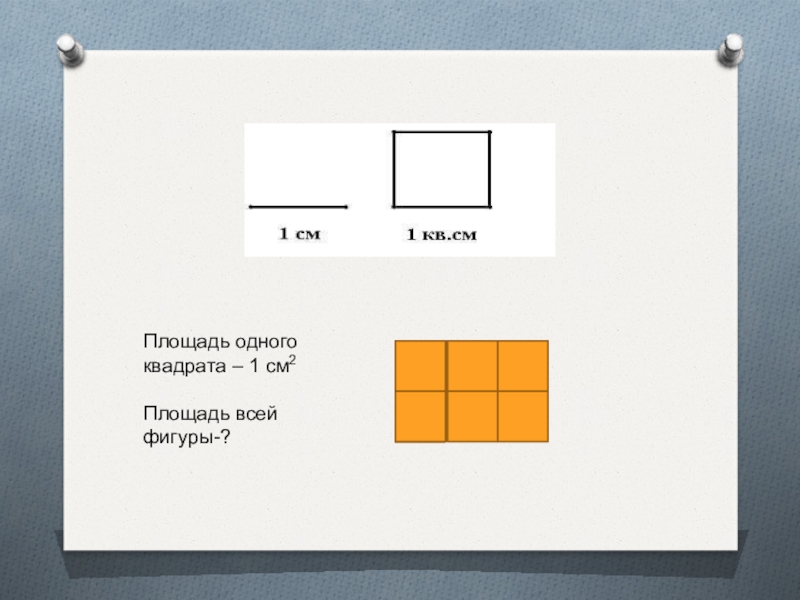
Слайд 5Площадь одного квадрата – 1 см2
Площадь всей фигуры-?
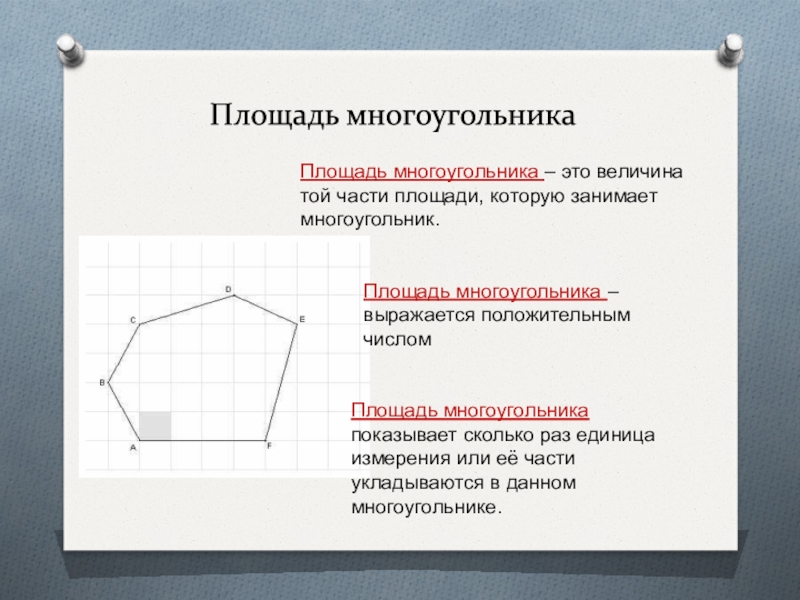
Слайд 7Площадь многоугольника
Площадь многоугольника – это величина той части площади, которую
занимает многоугольник.
Площадь многоугольника – выражается положительным числом
Площадь многоугольника показывает
сколько раз единица измерения или её части укладываются в данном многоугольнике.
Слайд 8Свойства площадей
Свойство1.
Равные многоугольники имеют равные площади
Задача
Площадь параллелограмма ABCD –
30 кв. см Чему равна площадь треугольника АВD?
Многоугольники, имеющие равные
площади называются равновеликими.
Слайд 9Свойство 2.
Если многоугольник составлен из нескольких многоугольников, то его
площадь равна сумме площадей этих многоугольников.
S1=S2+S3
Если многоугольник разрезан на несколько
многоугольников и из него составлен другой многоугольник, то такие многоугольники называют равносоставленными.
Слайд 10Верны ли утверждения?
Если два многоугольника равносоставленные, то они равновеликие?
Если два
многоугольника равновеликие, то они равносоставленные?
(выяснить кто из
известных математиков
доказал это утверждение?)
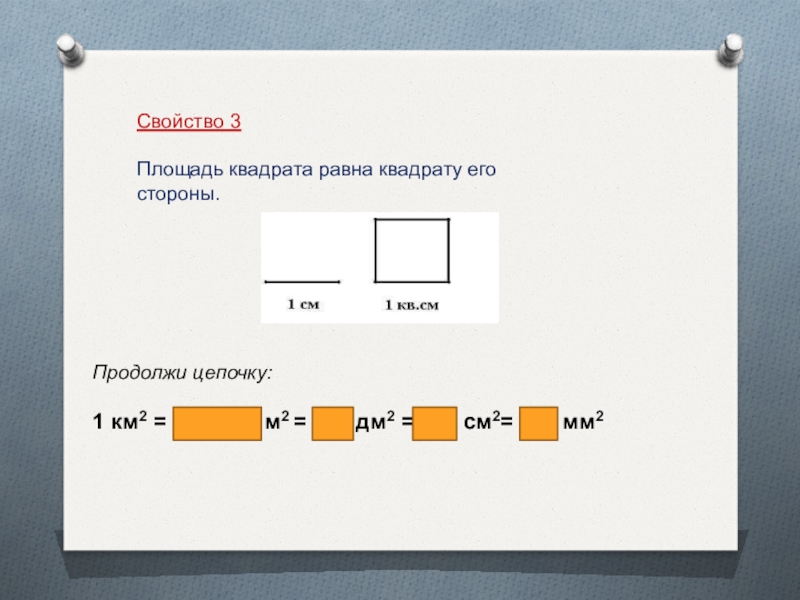
Слайд 11Свойство 3
Площадь квадрата равна квадрату его стороны.
Продолжи цепочку:
1 км2 =
1000000 м2 = 100 дм2 = 100 см2= 100 мм2
Слайд 13Палетка.
В тех случаях, когда измерение площади какой-нибудь фигуры не
требует большой точности, а также, когда фигура, площадь которой требуется
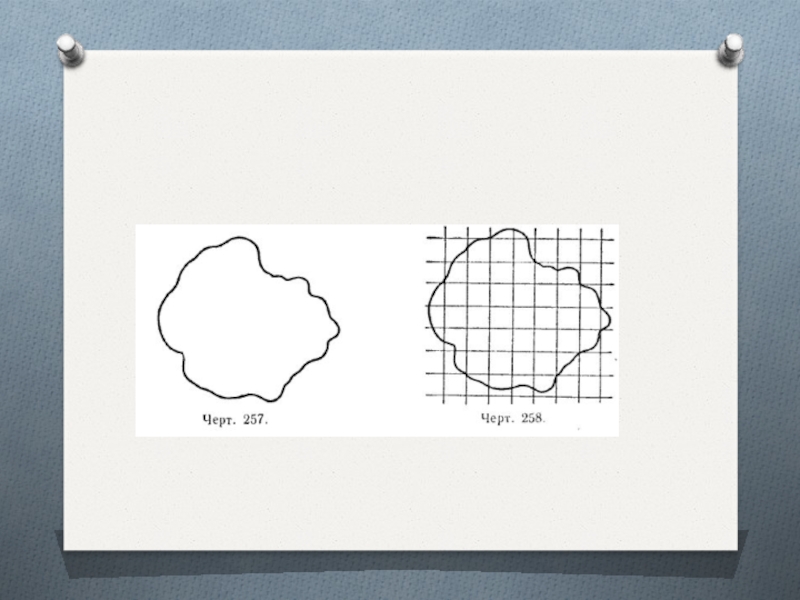
измерить, ограничена криволинейным контуром , для измерения площади употребляется особый прибор, называемый палеткой.
Палетка представляет собой прозрачную пластинку, на которую наносится масштабная квадратная сетка, например, со стороной квадрата, равной 1 см.
Слайд 15Эта пластинка накладывается на фигуру, площадь которой требуется измерить
Сначала
подсчитывается число квадратов, полностью укладывающихся в данной фигуре; на чертеже
их 26. Затем подсчитывается число квадратов, пересекаемых контуром фигуры; на чертеже их 21.
Каждый из неполных квадратов принимается за половину квадрата, таким образом, их общая площадь приближённо составит 21 : 2 = 10,5 квадрата.
Общее число квадратов, заключающихся в измеряемой фигуре, таким образом, составит 26 + 10,5 = 36,5 квадрата. Если, например, каждый квадрат в действительности соответствует 1 кв. м, то измеряемая площадь составит 36,5 кв. м.