Проекции прямых линий

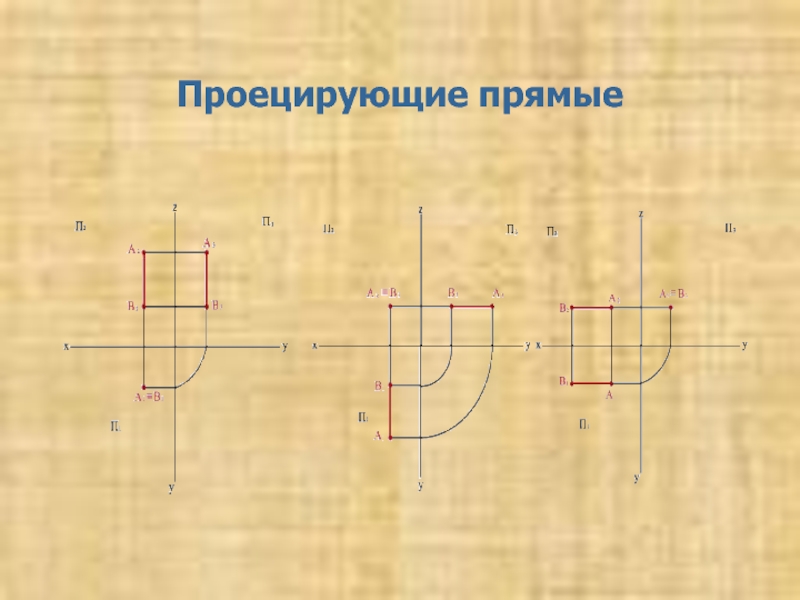
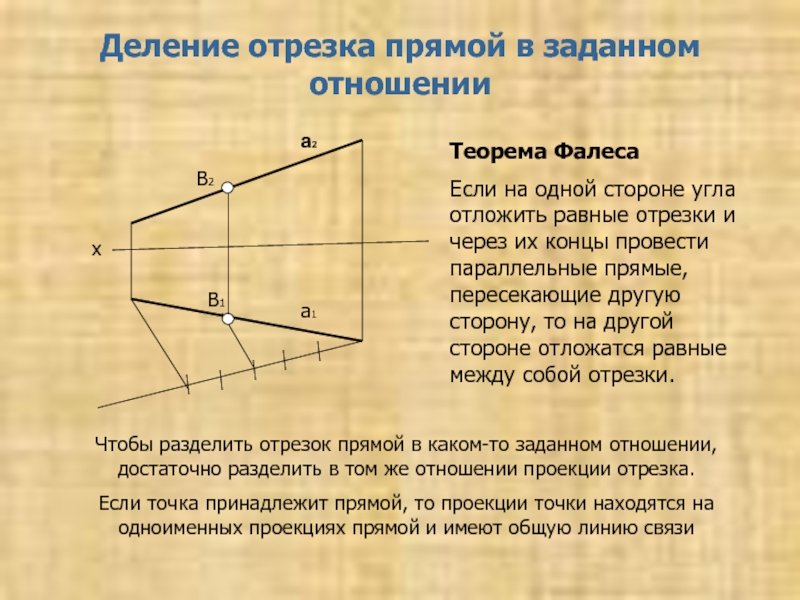
в заданном отношении
1.3 Следы прямой линии
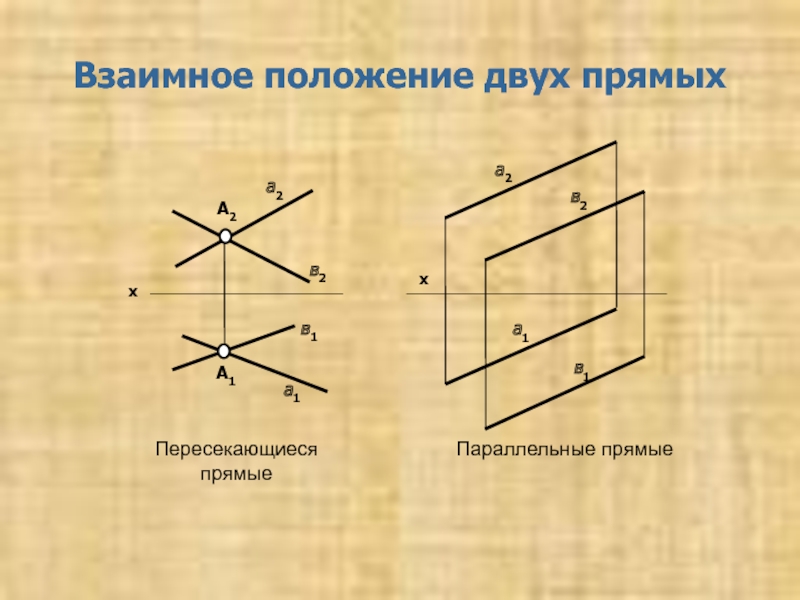
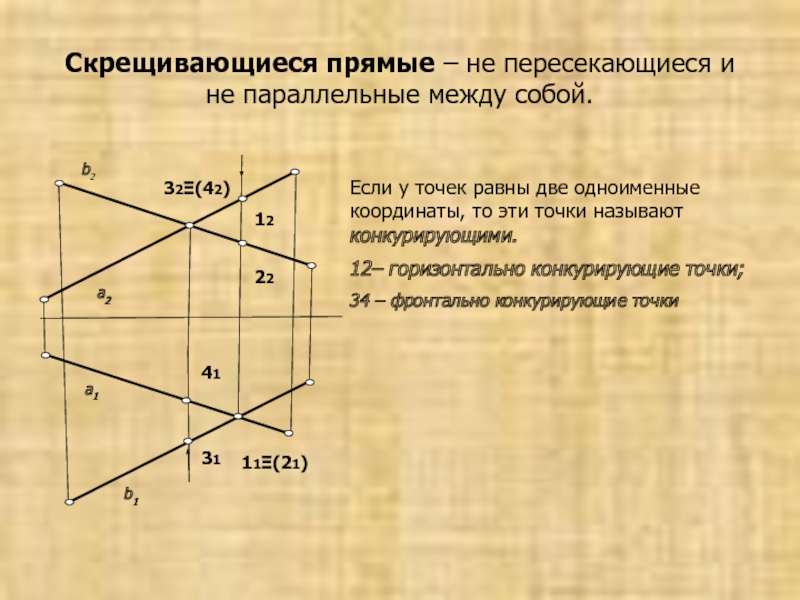
1.4 Взаимное положение двух прямых
2.

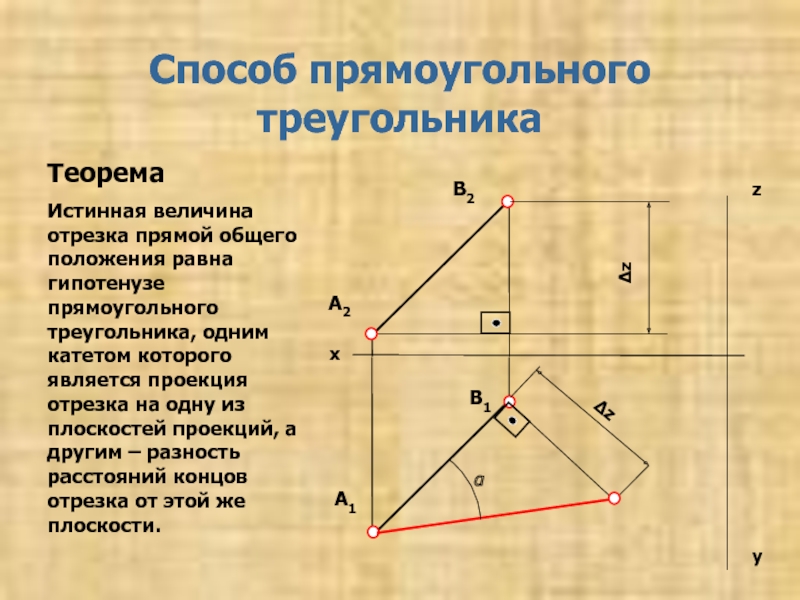
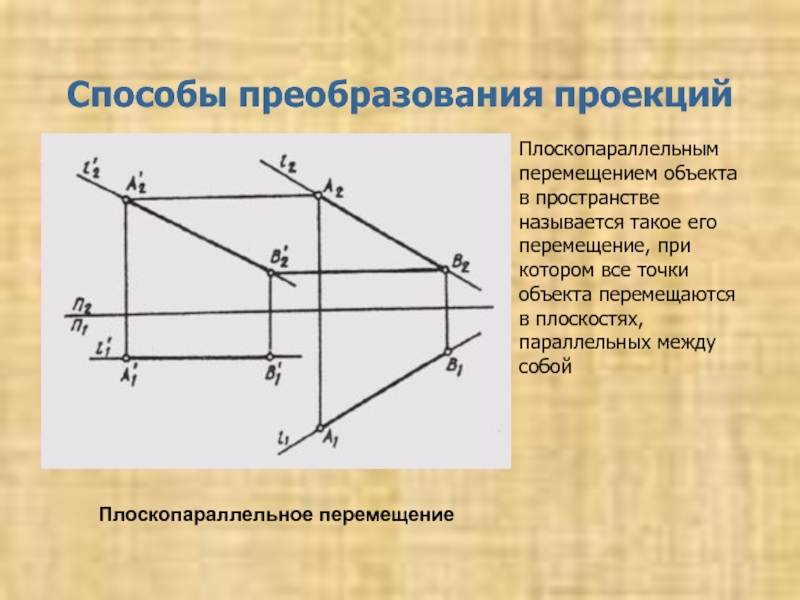
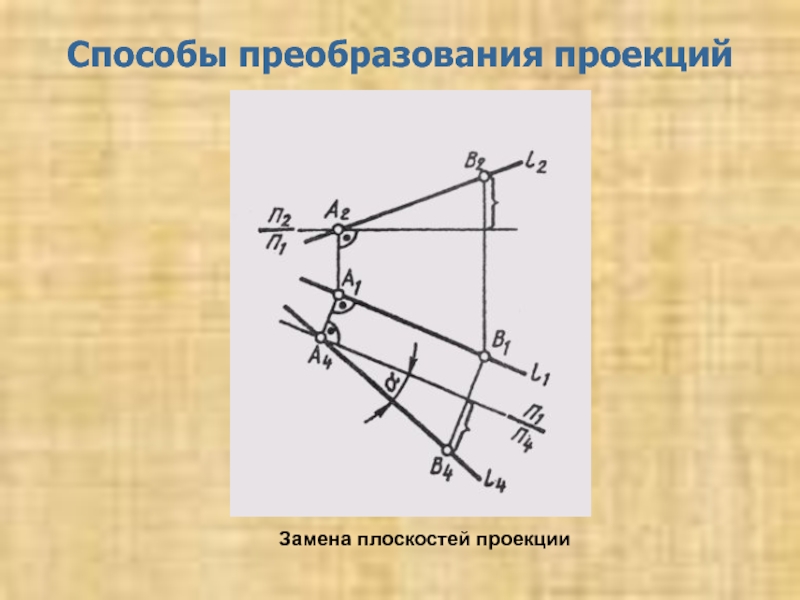
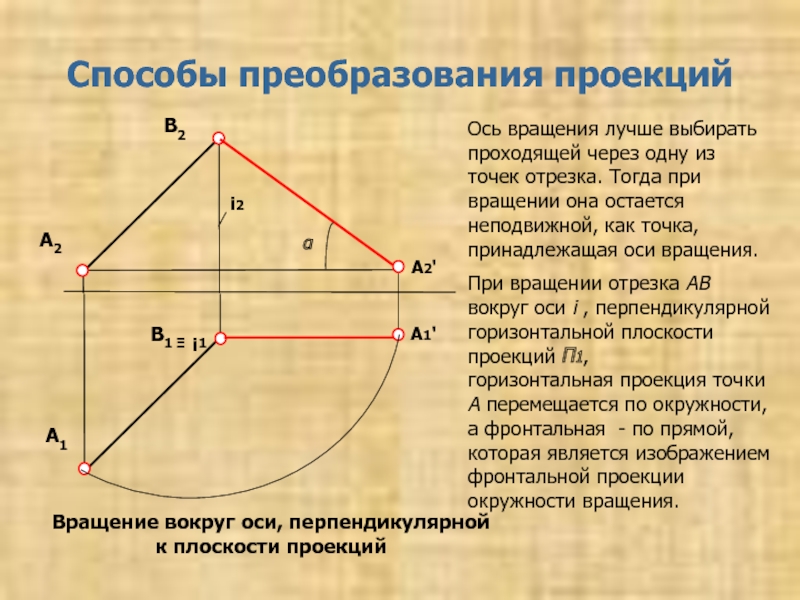
Определение натуральной величины отрезка и углов его наклона к плоскостям проекций
3. Способы преобразования проекций
4. Вопросы для самопроверки

ни одной из плоскостей проекций

проецирующая прямая.
АВ – фронтально проецирующая прямая.
ВС – профильно проецирующая прямая.

угла отложить равные отрезки и через их концы провести параллельные

прямые, пересекающие другую сторону, то на другой стороне отложатся равные между собой отрезки.

Чтобы разделить отрезок прямой в каком-то заданном отношении, достаточно разделить в том же отношении проекции отрезка.
Если точка принадлежит прямой, то проекции точки находятся на одноименных проекциях прямой и имеют общую линию связи

следом прямой.
В зависимости от того, с какой плоскостью проекции происходит

встреча прямой, следы обозначают и называют:
М - горизонтальный след прямой, Мz=0;
N - фронтальный след прямой, Ny=0;
Т - профильный след прямой, Tx=0;

проекций

плоскостей проекций

у точек равны две одноименные координаты, то эти точки называют

конкурирующими.
12– горизонтально конкурирующие точки;
34 – фронтально конкурирующие точки

определяется взаимное расположение отдельных геометрических элементов относительно друг друга. К

ним относятся задачи на определение взаимной принадлежности одних геометрических элементов другим и их пересечения.
Метрическими называют задачи на измерение отрезков, углов, определение истинной величины плоских фигур и т.п.

проекций
В
Угол между прямой и плоскостью определяется углом между прямой и

ее ортогональной проекцией на эту плоскость

прямоугольного треугольника, одним катетом которого является проекция отрезка на одну

из плоскостей проекций, а другим – разность расстояний концов отрезка от этой же плоскости.

занял частное положение относительно плоскостей проекций, которые при этом не

меняют своего положения в пространстве - способ плоскопараллельного перемещения.

2. Перемещением плоскостей проекций в новое положение по отношению, к которому проецируемый объект окажется в частном положении - способ замены плоскостей проекций.

его перемещение, при котором все точки объекта перемещаются в плоскостях,

параллельных между собой

лучше выбирать проходящей через одну из точек отрезка. Тогда при

вращении она остается неподвижной, как точка, принадлежащая оси вращения.
При вращении отрезка АВ вокруг оси i , перпендикулярной горизонтальной плоскости проекций П1, горизонтальная проекция точки А перемещается по окружности, а фронтальная - по прямой, которая является изображением фронтальной проекции окружности вращения.

могут быть расположены в пространстве две различные прямые?
Что такое след

прямой?
Как определить истинную величину отрезка по его комплексному чертежу?
Как разделить отрезок прямой в заданном отношении?
В чем состоит суть способа замены плоскостей проекций?
В чем состоит суть способа плоскопараллельного перемещения?