Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие производной. Дифференциал функции. Использование дифференциала в
Содержание
- 1. Понятие производной. Дифференциал функции. Использование дифференциала в
- 2. План лекции:Понятие производнойПравила дифференцирования, производная сложной функции
- 3. Понятие производной Производной функции f(x) называется
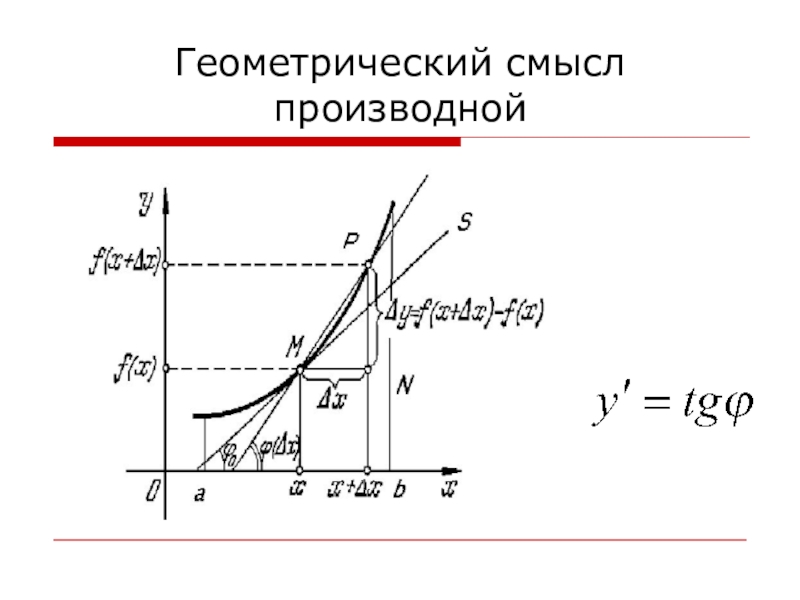
- 4. Геометрический смысл производной
- 5. Правила дифференцирования производная сложной функции
- 6. Таблица производных от основных функций
- 7. Исследование функций с помощью производных Значения аргумента,
- 8. Исследование функций с помощью производных В критической
- 9. Задание: Найти интервалы монотонности и экстремумы функцииДана функцияФункция не определена при х=2
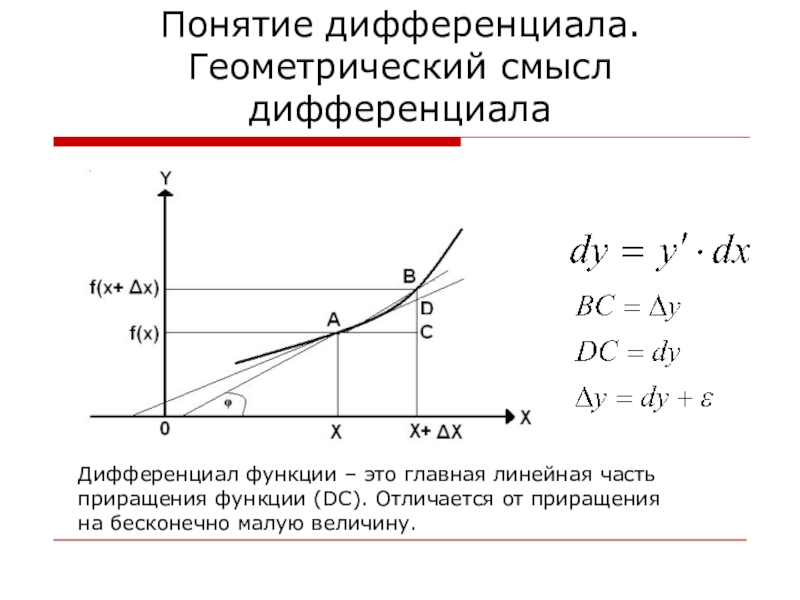
- 10. Понятие дифференциала. Геометрический смысл дифференциалаДифференциал функции –
- 11. Использование дифференциала в приближенных вычисленияхДля нахождения приближенного
- 12. БЛАГОДАРЮ ЗА ВНИМАНИЕ
- 13. Скачать презентанцию
План лекции:Понятие производнойПравила дифференцирования, производная сложной функции Таблица производных от основных функцийПонятие дифференциала. Частные производные. Полный дифференциалИспользование дифференциала в приближенных вычислениях
Слайды и текст этой презентации
Слайд 1Понятие производной. Дифференциал функции. Использование дифференциала в приближенных вычислениях.
Лекция2
Слайд 2План лекции:
Понятие производной
Правила дифференцирования, производная сложной функции
Таблица производных от
основных функций
вычислениях
Слайд 3Понятие производной
Производной функции f(x) называется предел отношения приращения
функции к приращению аргумента при стремлении последнего к нулю, т.е.
Слайд 7Исследование функций с помощью производных
Значения аргумента, при котором производная
равна 0, называются стационарными точками. Стационарные точки и точки, в
которых производная не существуют – критические точки.На интервале положительности производной функция возрастает, а на интервале отрицательности – убывает.
Слайд 8Исследование функций с помощью производных
В критической точке, отделяющей интервал
возрастания от интервала убывания, функция имеет максимум (производная меняет знак
с плюса на минус).В критической точке, отделяющей интервал убывания от интервала возрастания , функция имеет минимум (производная меняет знак с минуса на плюс ).
Слайд 9Задание: Найти интервалы монотонности и экстремумы функции
Дана функция
Функция не определена
при х=2
Слайд 10Понятие дифференциала. Геометрический смысл дифференциала
Дифференциал функции – это главная линейная
часть
приращения функции (DC). Отличается от приращения
на бесконечно малую
величину.
Слайд 11Использование дифференциала в приближенных вычислениях
Для нахождения приближенного значения приращения функции
Для
нахождения приближенного значения функции в заданной точке
Для вычисления погрешностей
