Последовательное соединение RLC- элементов

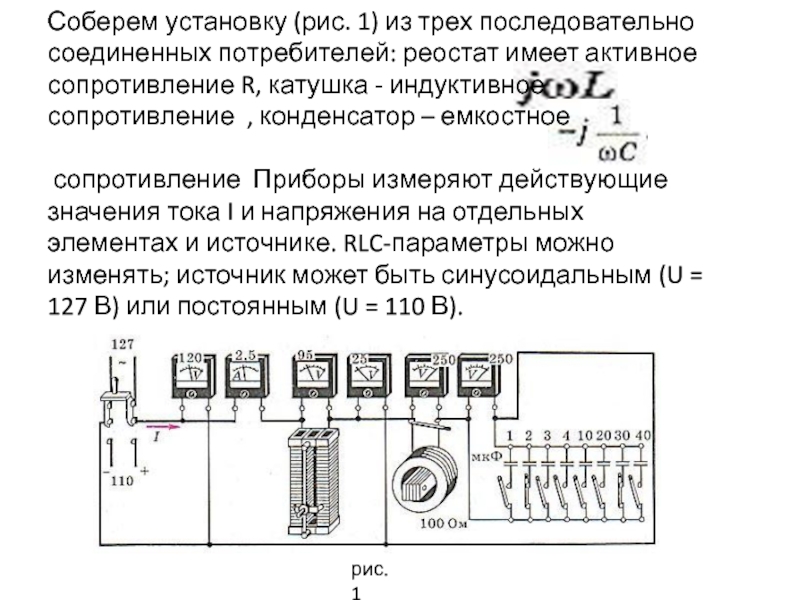
имеет активное сопротивление R, катушка - индуктивное сопротивление  , конденсатор

– емкостное

сопротивление  Приборы измеряют действующие значения тока I и напряжения на отдельных элементах и источнике. RLC-параметры можно изменять; источник может быть синусоидальным (U = 127 В) или постоянным (U = 110 В).

рис. 1

возрастает, а затем спадает до нуля: происходит заряд емкости током,

проходящим через обмотку катушки индуктивности, которая по закону электромагнитной индукции (самоиндукции) сначала препятствует его возрастанию, а затем его уменьшению. Чем больше R, L и C, тем дольше будет длиться этот процесс; чем меньше R, тем более выражается колебательный характер этого процесса. Колебания возникают вследствие того, что ранее накопленная энергия магнитного поля катушки переходит в энергию электрического поля конденсатора и далее наоборот; колебания затухают благодаря тому, что часть их энергии необратимо поглощается активным сопротивлением R. Чем больше R, тем меньше колебания по амплитуде, но и тем дольше происходит заряд емкости (конденсатора).

1). Если f = 50 Гц, С = 32 мкФ,

L = 0,32 Гн, R = 38 Ом, в стабильном режиме вынужденных колебаний приборы покажут: U = 127 В, UBC = 25 В, I = 2,5 А. Как видим, для действующих значений напряжений второй закон Кирхгофа не выполняется


поскольку эти напряжения векторные и имеют свои начальные фазы. Законы Кирхгофа справедливы для комплексной формы выражения напряжений (рис. 2):

   в алгебраической, показательной и тригонометрической формах:




Где

Для

и

комплексное сопротивление Z  составит

определяет аргумент комплексного полного сопротивления Z , т.е.  Векторные диаграммы токов и

на комплексной плоскости в соответствии с уравнением Кирхгофа, учитывая сдвиг фаз между напряжениями 
 и током I  (рис.3).

сопротивление. Ток I отстает от напряжения U, и сдвиг фаз положительный; диаграмма (б)

- для цепи, в которой преобладает емкостное сопротивление, ток I опережает напряжение U , и сдвиг фаз  отрицательный. От треугольников напряжений, разделив каждую сторону треугольника на ток, переходим к подобному ему треугольнику сопротивлений. Мгновенная мощность, в зависимости от знака  , идентична мощности RL-цепи (  > 0) или RC-цепи (   < 0). Активная мощность

= UI - полная мощность.
Величина   

является реактивной мощностью. Она положительна, когда  > 0, и отрицательна, когда   < 0. Абсолютное значение

сопряженный комплекс тока. Треугольник напряжений подобен соответствующему треугольнику сопротивлений (рис.

4).