Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение графиков функции y = sinx и y = cosx . 10 класс
Содержание
- 1. Построение графиков функции y = sinx и y = cosx . 10 класс
- 2. Цели : 1)Повторить правила преобразований функции:y
- 3. 2) Научиться строить графики вида y = f(x + t) + m3)Закрепить умения, выполнив практические задания.
- 4. Построение графиков функций у = sinx + m и у = cosх + m.
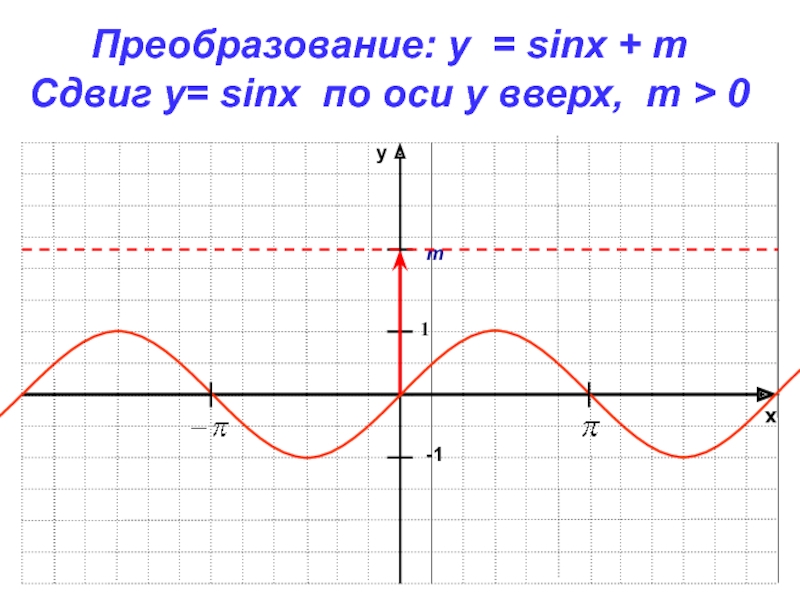
- 5. xy-11Преобразование: y = sinx + mСдвиг у= sinx по оси y вверх, m > 0m
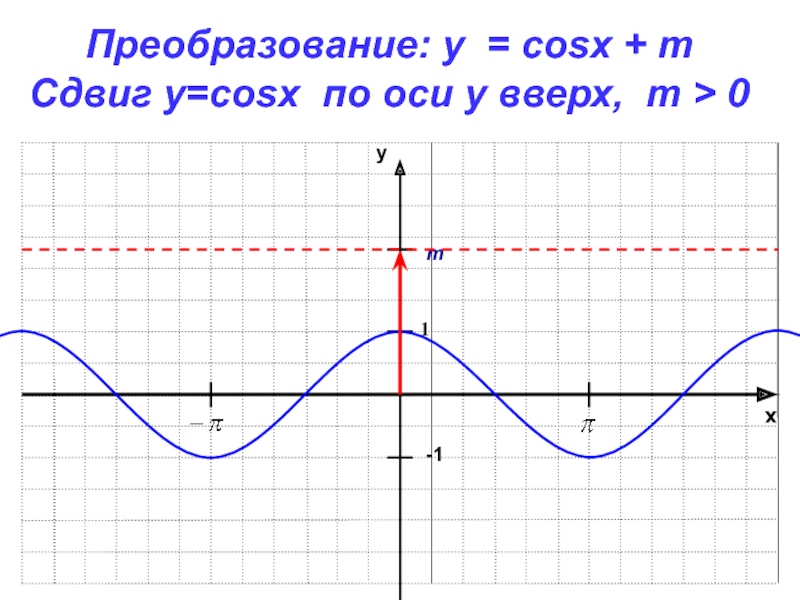
- 6. xy-11Преобразование: y = cosx + mСдвиг у=cosx по оси y вверх, m > 0m
- 7. xy-11Преобразование: y = sinx + mСдвиг у= sinx по оси y вниз, m < 0m
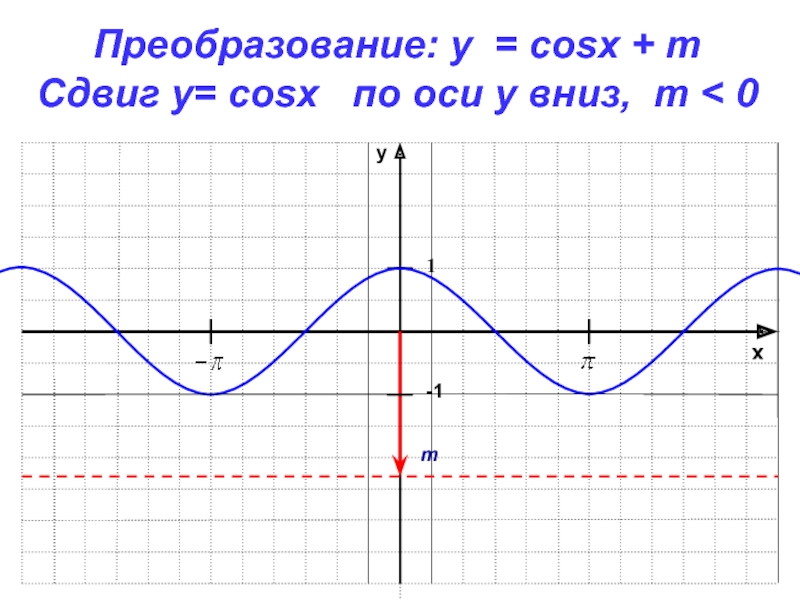
- 8. xy-11Преобразование: y = cosx + mСдвиг у= cosx по оси y вниз, m < 0m
- 9. Параллельный перенос графика вдоль оси ОуГрафик функции
- 10. Задание:Постройте в одной координатной плоскости графики функций:
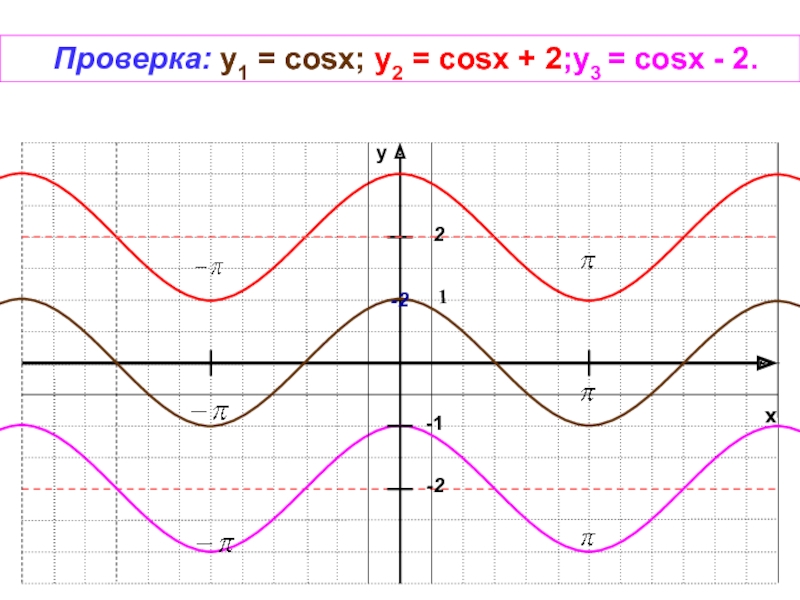
- 11. xy-11-2Проверка: y1 = sinx; у2 = sinx + 2; у3 = sinx - 2.2
- 12. Задание:Постройте в одной координатной плоскости графики функций:
- 13. xy-11-2 Проверка: y1 = cosx; у2 = cosx + 2;у3 = cosx - 2.2-2
- 14. Построение графиков функций y= sin(x+t) и у = cos(x+ t).
- 15. xy-11Преобразование: y = sin(x + t)сдвиг у=f(x) по оси х влево, t > 0 t
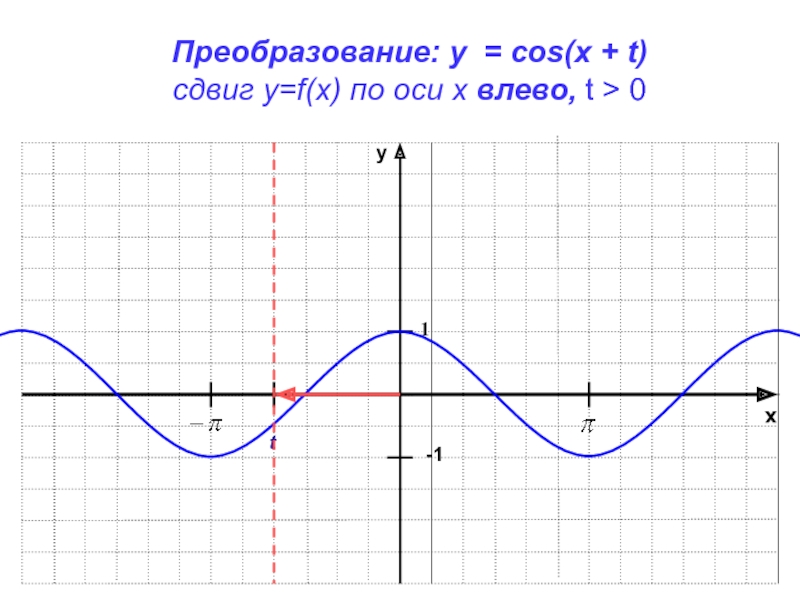
- 16. xy-11Преобразование: y = cos(x + t)сдвиг у=f(x) по оси х влево, t > 0t
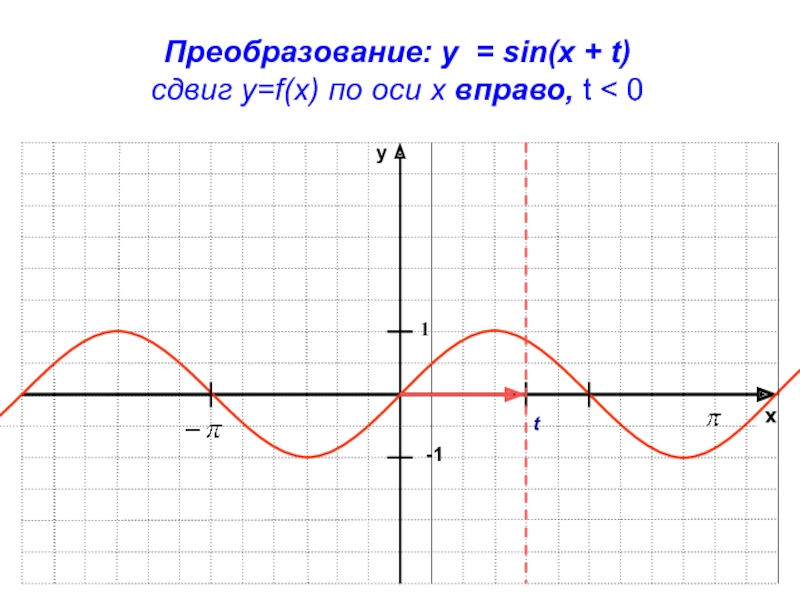
- 17. xy-11Преобразование: y = sin(x + t)сдвиг у=f(x) по оси х вправо, t < 0 t
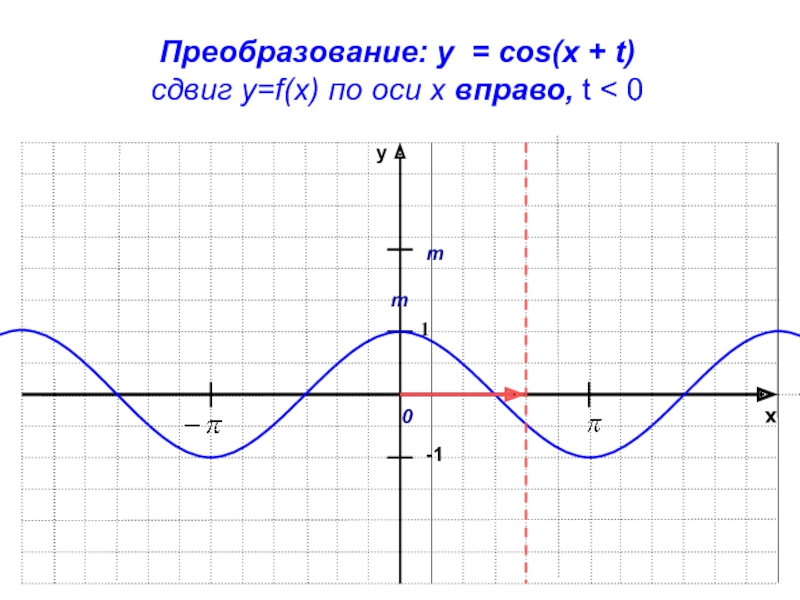
- 18. xy-11Преобразование: y = cos(x + t)сдвиг у=f(x) по оси х вправо, t < 0mm0
- 19. Параллельный перенос графика вдоль оси Ох
- 20. Задание:Постройте в одной координатной плоскости графики функций:
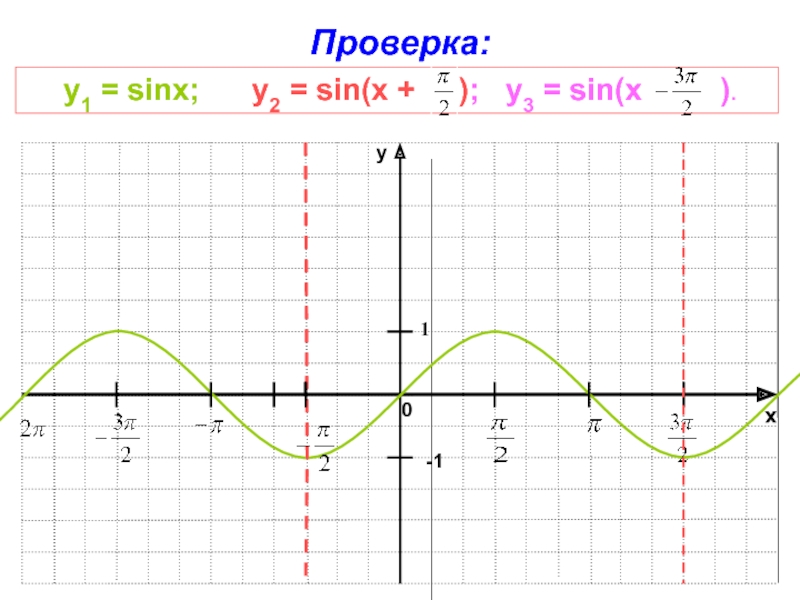
- 21. xy1Проверка:y1 = sinx; у2 =
- 22. Задание: Постройте в одной
- 23. xy-11Проверка: y1 = cosx; у2 =
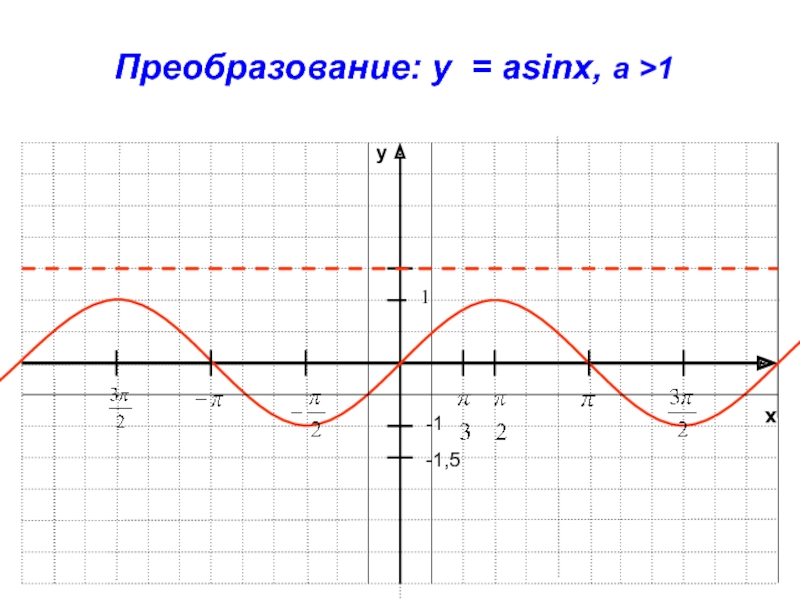
- 24. Построение графиков функций у = asinx
- 25. xy-1Преобразование: y = asinx, a >11-1,5
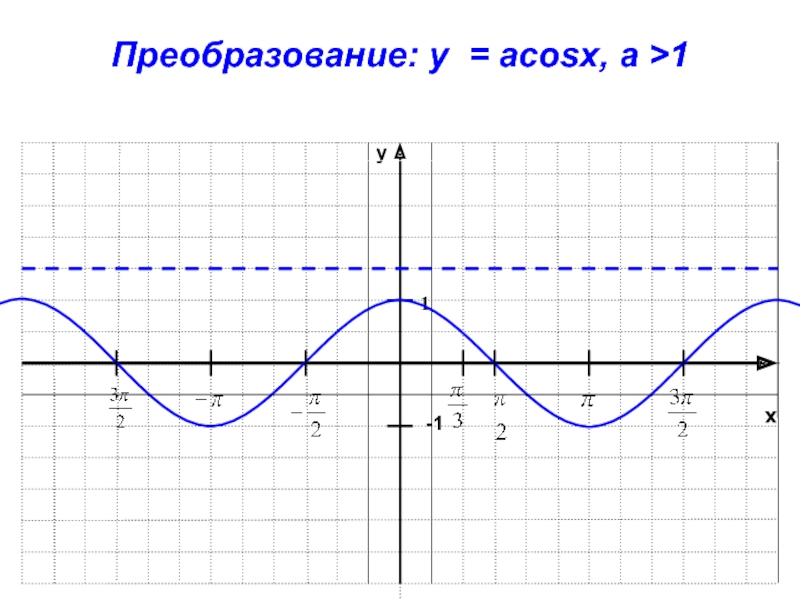
- 26. xy-11Преобразование: y = acosx, a >1
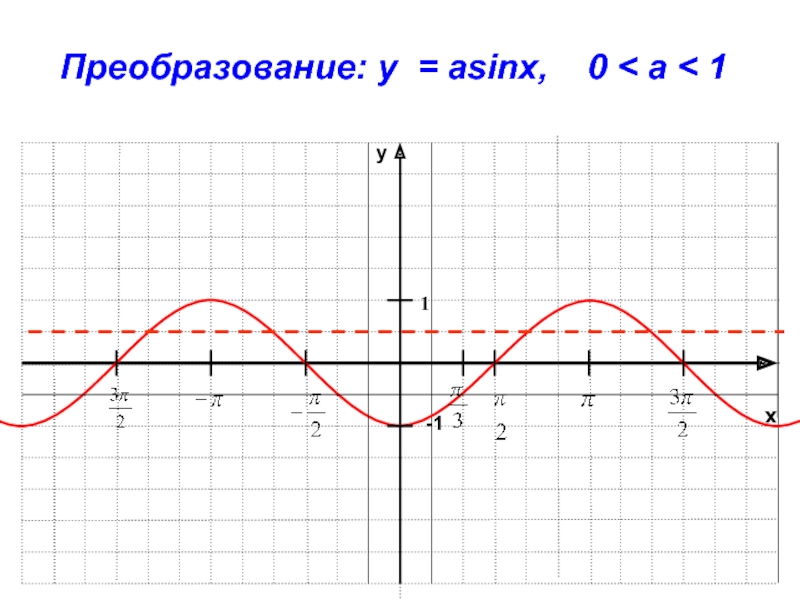
- 27. xy-11Преобразование: y = asinx, 0 < a < 1
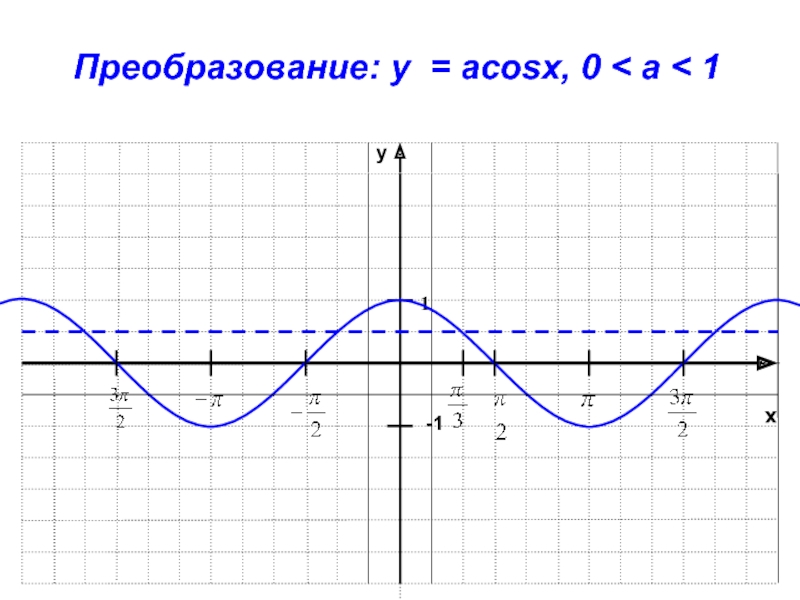
- 28. xy-11Преобразование: y = acosx, 0 < a < 1
- 29. Построение графика функции у=аf(x) График функции у=аf(x)
- 30. Постройте в одной координатной плоскости графики функций:y1
- 31. xy-11Проверка: y1 = sinx; у2 = 2sinx;
- 32. Постройте в одной координатной плоскости графики функций:
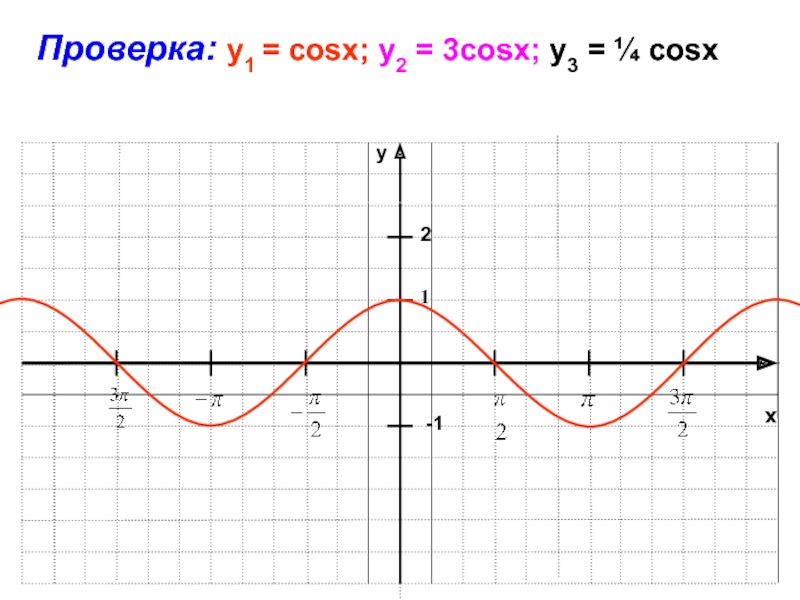
- 33. xy-11Проверка: y1 = cosx; у2 = 3cosx;
- 34. Постройте графики функций: Задание: у2
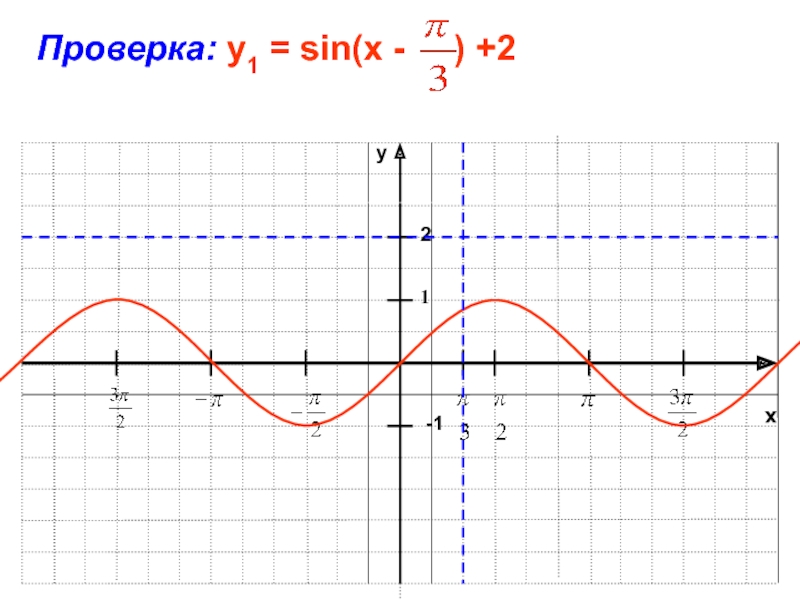
- 35. xy-11Проверка: у1 = sin(x -
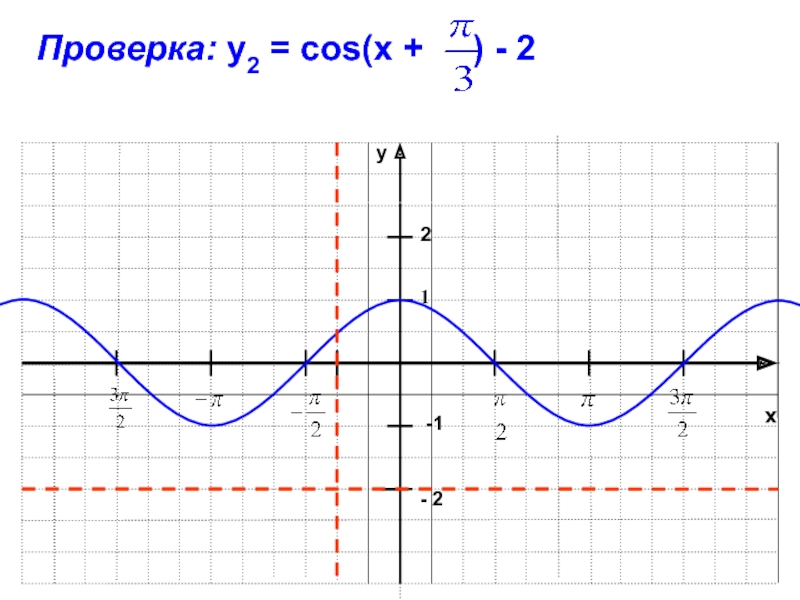
- 36. xy-11Проверка: у2 = cos(x +
- 37. Вывод: График функции y=f(x + t) +
- 38. Постройте самостоятельно графики функций: Вариант
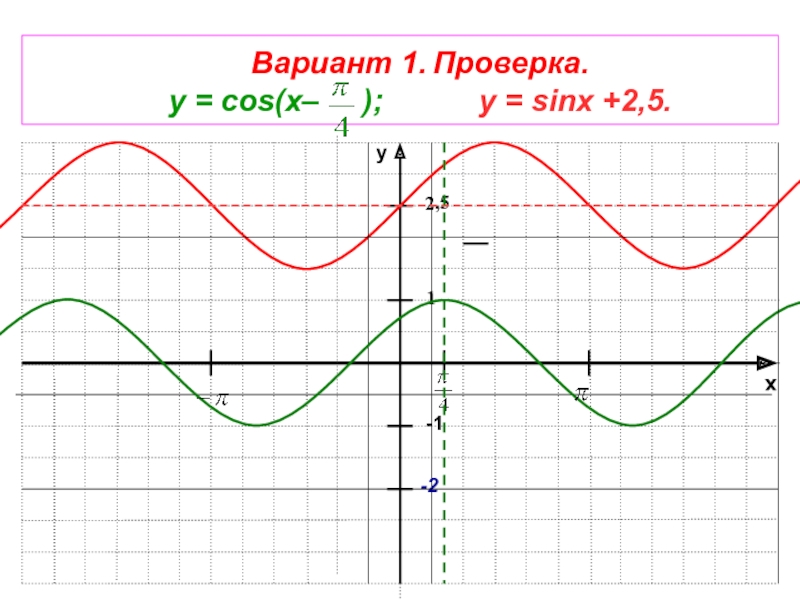
- 39. xy-11-2Вариант 1. Проверка. у = cos(x–
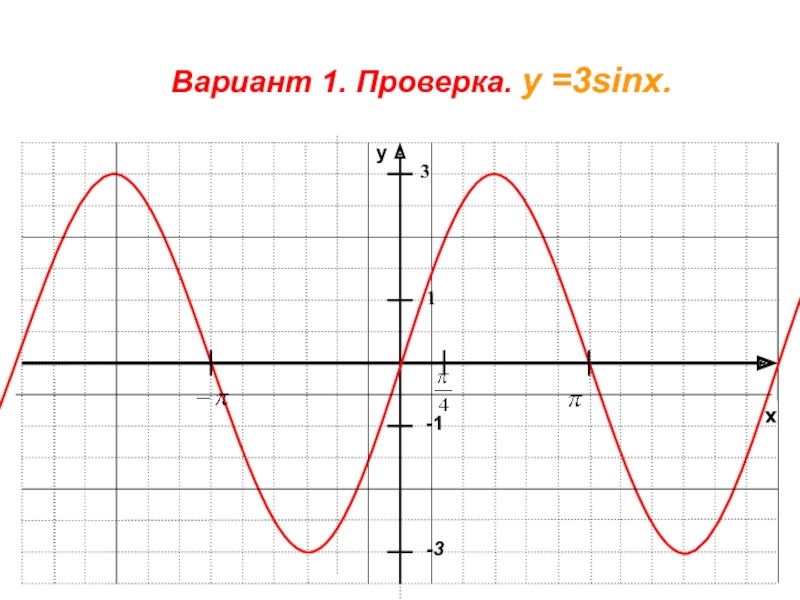
- 40. xy-11-3Вариант 1. Проверка. у =3sinx. 3
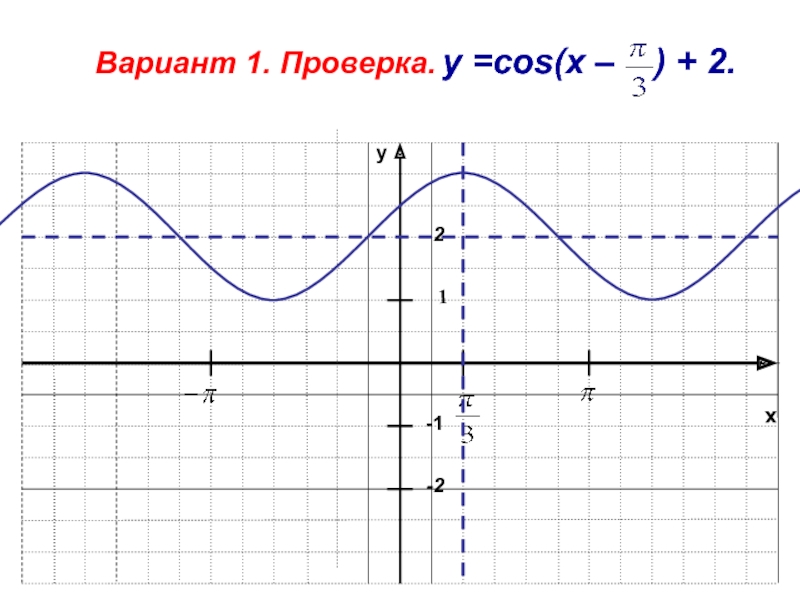
- 41. xy-11-2Вариант 1. Проверка. у =cos(x – ) + 2.2
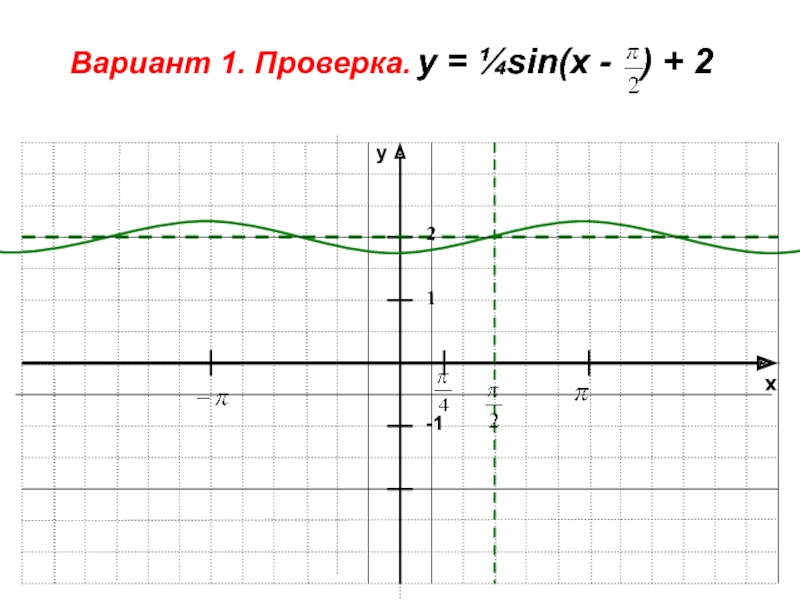
- 42. xy-11Вариант 1. Проверка. у = ¼sin(x - ) + 22
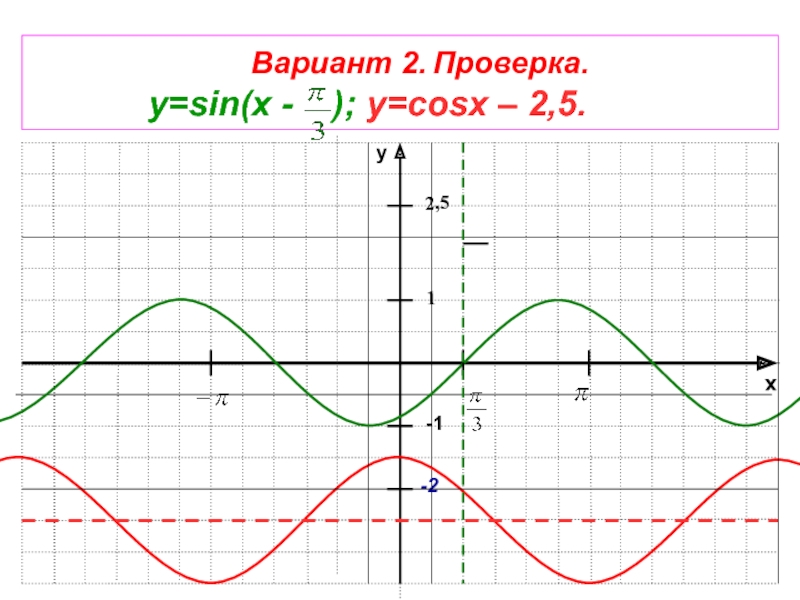
- 43. xy-11-2Вариант 2. Проверка. y=sin(x - ); y=cosx – 2,5.2,5
- 44. xy-11Вариант 2. Проверка. у = ½cosx
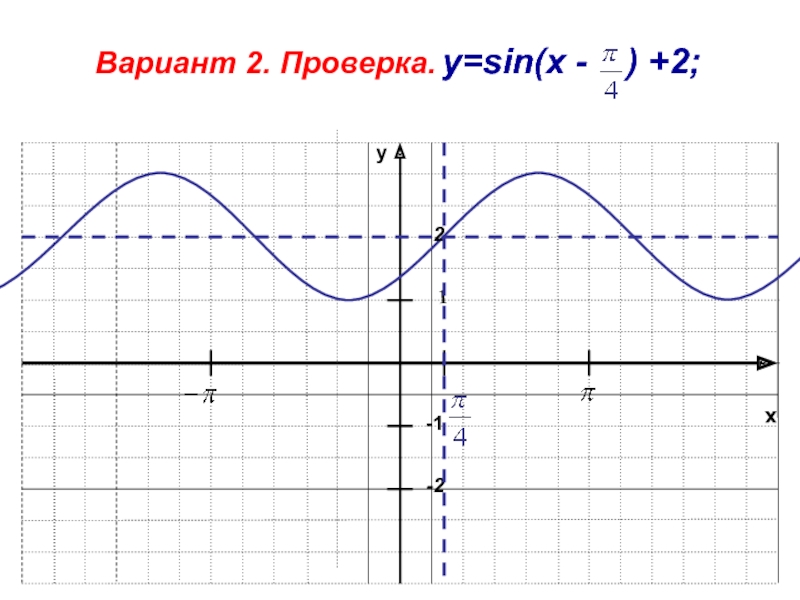
- 45. xy-11-2Вариант 2. Проверка. y=sin(x - ) +2;2
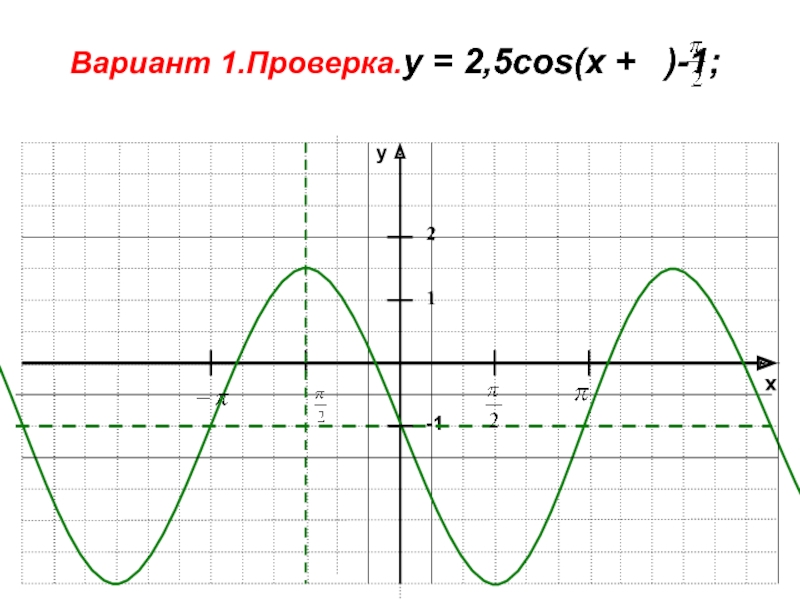
- 46. xy-11Вариант 1.Проверка.у = 2,5cos(x + )-1; 2
- 47. Скачать презентанцию
Цели : 1)Повторить правила преобразований функции:y = f(x) + my = f(x + t)y = af(x)
Слайды и текст этой презентации
Слайд 32) Научиться строить графики вида
y = f(x + t)
+ m
3)Закрепить умения, выполнив практические задания.
Слайд 9Параллельный перенос графика вдоль оси Оу
График функции y=f(x)+m получается параллельным
переносом графика функции y=f(x), вверх на m единиц, если m>0,
или вниз, если m<0.
Слайд 10Задание:
Постройте в одной координатной плоскости графики функций:
y1 =
sinx;
у2 = sinx + 2;
у3 = sinx - 2.Слайд 12Задание:
Постройте в одной координатной плоскости графики функций:
y1 =
cosx;
у2 = cosx + 2;
у3 = cosx - 2.Слайд 19
Параллельный перенос графика вдоль оси Ох
График функции y = f(x
+ t) получается параллельным переносом графика функции y=f(x) по оси
х на |t| единиц масштаба влево, если t > 0и вправо, если t < 0.
Слайд 20Задание:
Постройте в одной координатной плоскости графики функций:
y1 =
sinx;
у2 = sin(x +
);у3 = sin(x ).
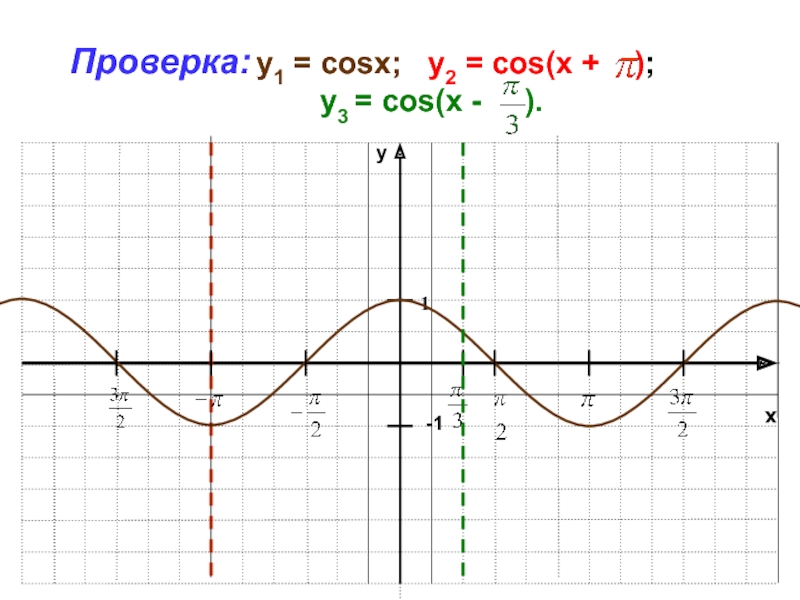
Слайд 22
Задание:
Постройте в одной координатной плоскости графики функций:
1)y1 =
cosx;
2)у2 = cos(x + );
3) у3 = cos(x -
).Слайд 29Построение графика функции у=аf(x)
График функции у=аf(x) получаем растяжением графика
функции у=f(x) с коэффициентом а от оси Ох,если а>1 и
сжатием к оси Ох с коэффициентом 0< а <1.Слайд 37
Вывод:
График функции y=f(x + t) + m может быть
получен из графика функции y=f(x) с помощью двух последовательных сдвигов
на t единиц вдоль оси Ох и на m единиц вдоль оси Оу.
Слайд 38Постройте самостоятельно графики функций:
Вариант 1.
Вариант 2.
у =
cos(x– ); 1. y=sin(x - );у = sinx +2,5; 2. y=cosx – 2,5;
у = 3sinx 3. у = ½cosx
у =cos(x – ) + 2; 4. y=sin(x - ) +2;
5. у = ¼sin(x - ) + 2; 5. y=3cos(x + )-1;