Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение классификации для нормального распределения
Содержание
- 1. Построение классификации для нормального распределения
- 2. Построение классификации для нормального распределения матрица ковариации
- 3. Построение классификации для нормального распределения Если взять
- 4. Построение классификации для нормального распределения Как строится
- 5. Построение классификации для нормального распределения для удобства
- 6. простейшая дискриминантная функция Построение классификации для нормального
- 7. Построение классификации для нормального распределения Области классов
- 8. Утверждение:Для данной решающей функции вектор лежит ровно
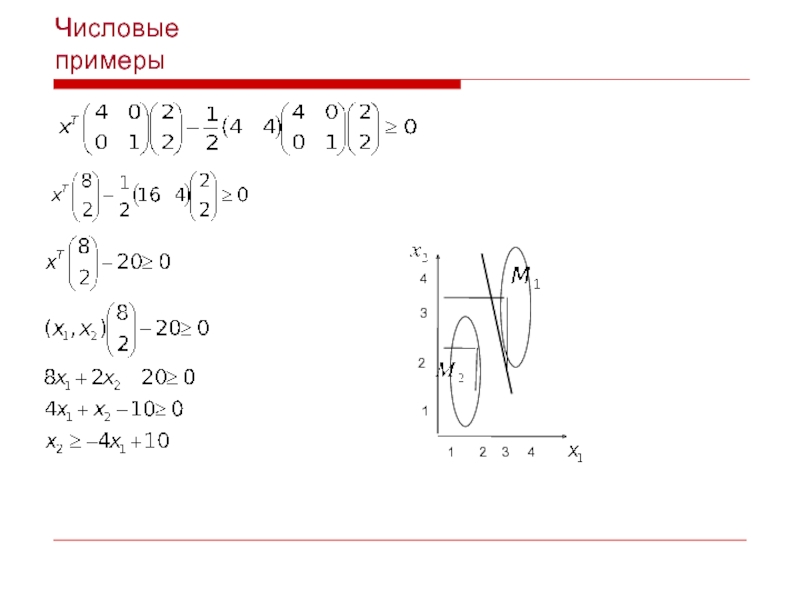
- 9. Числовые примеры Рассмотрим случай, когда матрица не
- 10. Числовые примеры
- 11. Слайд 11
- 12. Числовые примеры
- 13. Числовые примеры Найдем уравнение эллипса равной плотности вероятностей
- 14. в общем виде:соответственно полуоси:Числовые примеры
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Классификация объекта для двух нормальных распределений с
равными матрицами ковариации и
разными математическими
для нормального распределения Слайд 2Построение классификации для нормального распределения
матрица ковариации
ковариация компонент
i и j;
Где:
- дисперсия компоненты i
Матрица может быть
определена следующим образом:Слайд 3Построение классификации для нормального распределения
Если взять f(x) = const
и выбрать const таким образом, чтобы она была маленькой, то
- определяет эллипсы в многомерном пространстве, дающие описание
многомерной плотности с помощью линий равной плотности вероятности.
Если взять f(x) = const и выбрать const таким образом,
чтобы она была маленькой, то
Слайд 4Построение классификации для нормального распределения
Как строится правило решения для
классификации двух классов?
Предполагается, что есть 2 класса.
,
где К- порог.
Решение строится на основе функции правдоподобия:
Слайд 5Построение классификации для нормального распределения
для удобства работы прологарифмируем:
Преобразовав
выражение, получим правило в следующем виде:
это уравнение линейной дискриминантной функции,
полученной на основе Байесовского решающего правила.
Для дальнейшего анализа будем считать:
C (2/1) =C (1/2)
Слайд 6
простейшая дискриминантная
функция
Построение классификации для нормального распределения
Пусть
Размерность
пространства возьмем равную 2 .
Тогда получаем следующее правило решения
W – весовой вектор
Слайд 7Построение классификации для нормального распределения
Области классов представляют собой сферы.
Положение этой плоскости определяется вектором W.
Решающая плоскость перпендикулярна вектору
Уравнение решающей плоскости:
- это уравнение сферы можно свести к выражению
Слайд 8Утверждение:
Для данной решающей функции вектор
лежит ровно на середине
вектора
Таким образом, в случаях
a)
b)
решение выглядит следующим
образом:Построение классификации для нормального распределения
Слайд 9Числовые примеры
Рассмотрим случай, когда матрица не является единичной:
нужно
получить уравнение для решающей функции:
Вариант 1
Решение варианта 1: