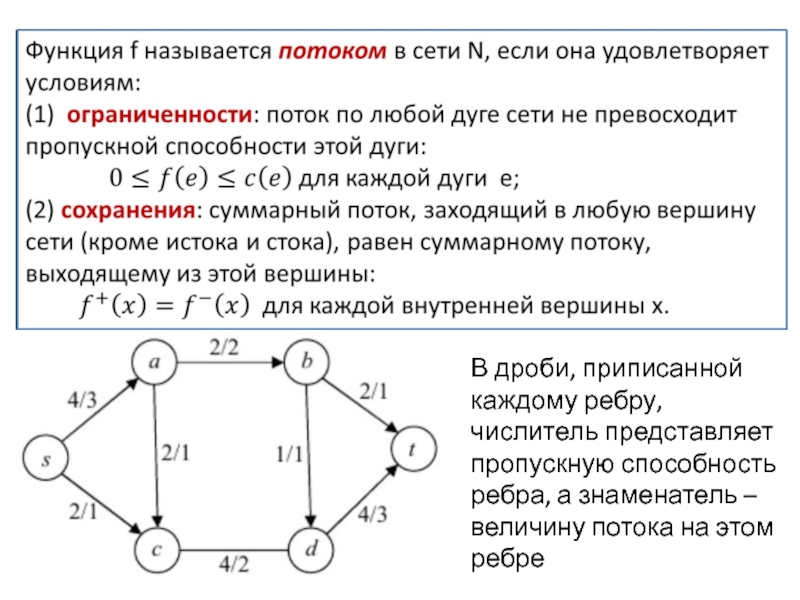
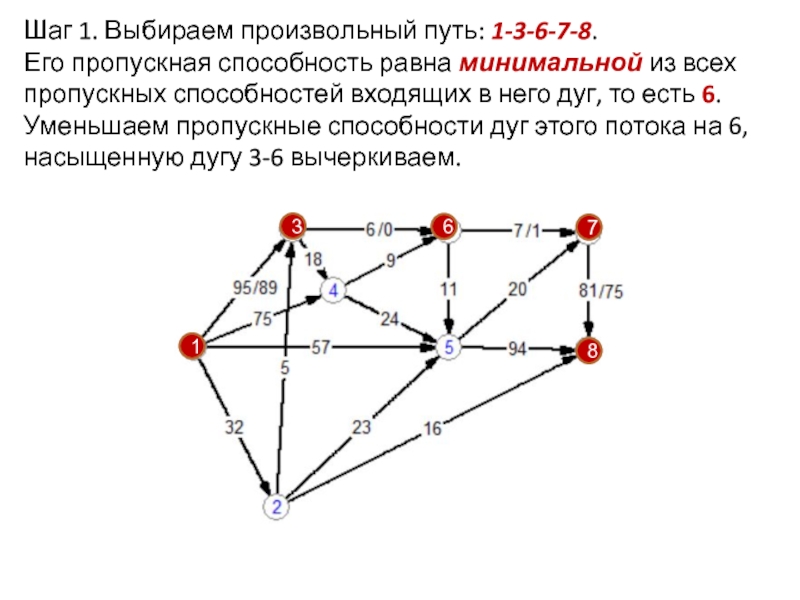
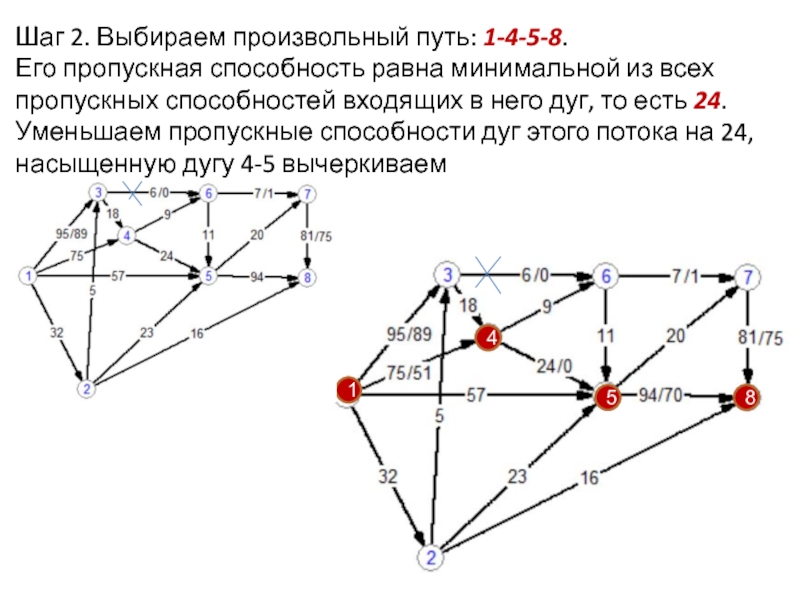
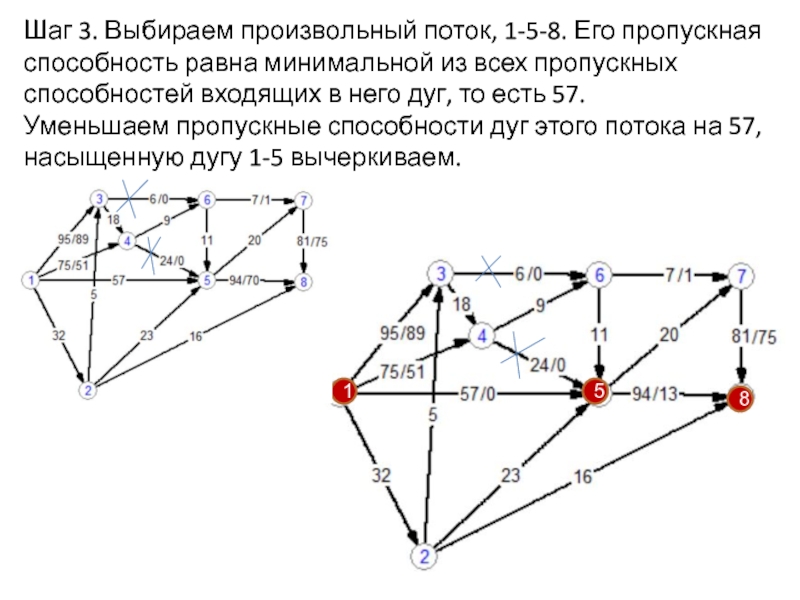
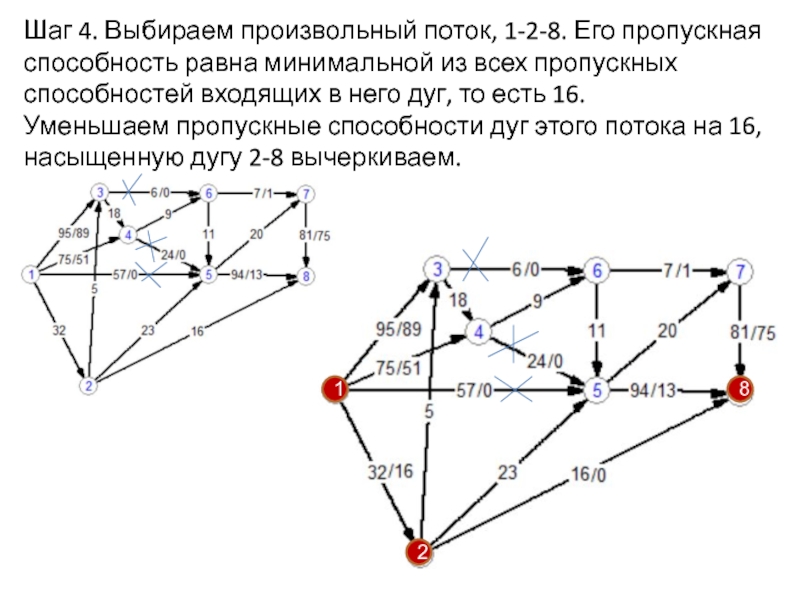
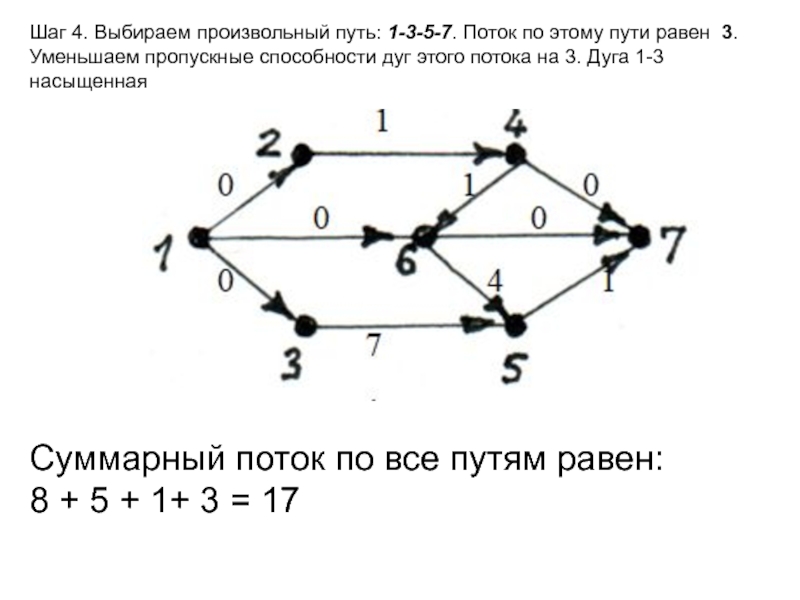
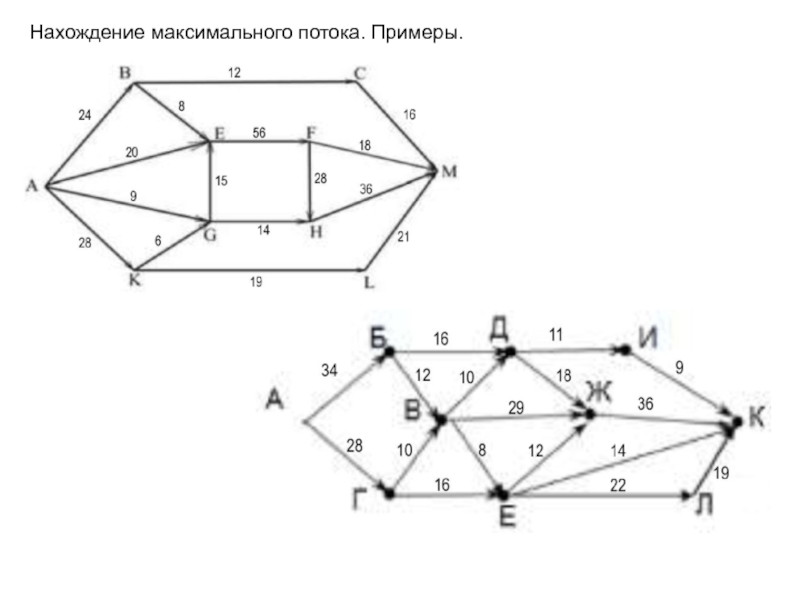
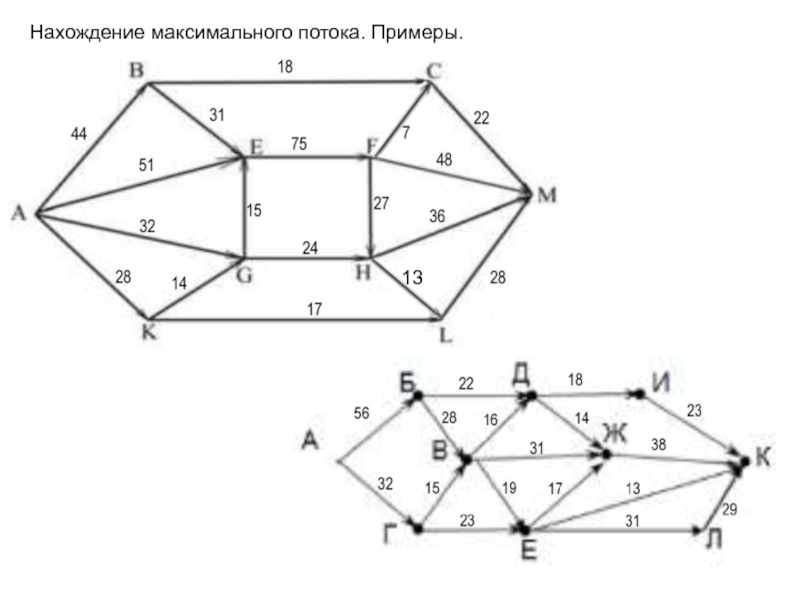
приписано положительное число c(e), называемое пропускной способностью ребра;
2) выделены
две вершины s и t, называемые соответственно источником и стоком, при этом E+(s) = E−(t)= ∅ - то есть из источника дуги только выходят, а в сток только входят. На этом занятии будем рассматривать ориентированные графы без петель и кратных ребер. Для вершины x множество всех входящих в нее ребер обозначается через E+(x), а множество выходящих – через E−(x).