Слайд 2Основные задачи
Если приписать каждой дуге ориентированного графа поток
некоторого вещества, граф становится удобной моделью при исследовании целого ряда
проблем в транспорте, связи и других областях, связанных с действительным или воображаемым движением товаров, информации или людей.
Исследуется две основные задачи:
максимизация суммарного потока между двумя заданными вершинами при условии, что поток через каждую дугу ограничен сверху и снизу;
задача нахождения ограниченных потоков с минимальной стоимостью, когда каждой дуге приписана стоимость единицы потока.
Слайд 3Ограничим определение ориентированного графа
наличие петель недопустимо
если существует дуга из vi
в vj, то дуги из vj в vi нет
ориентированный граф
должен быть связанным
Слайд 4Разделяющие множества
Пусть G = (V, E) — связный граф и F
E — подмножество множества его ребер. При этом F
называется разделяющим множеством тогда и только тогда, когда подграф G = (V, E – F) несвязен.
Разделяющие множества всегда существуют (если граф имеет по меньшей мере две вершины), так как всегда можно положить F = E. Очевидно, что граф может быть разбит разделяющим множеством на более чем две компоненты.
Слайд 5Разрезы
Если задан связный граф G = (V, E) и множество его
вершин разбито на два непустых подмножества А и A, множество
ребер, соединяющих A с A, называется разрезом.
Для любого множества A это множество ребер будет непусто в силу связности графа G, и следовательно, разрез определен. Для любого заданного графа совокупность разрезов, определенных различными множествами A, образует подкласс класса всех разделяющих множеств и, более того, любое разделяющее множество содержит, по крайней мере, один разрез в качестве своего подмножества.
Слайд 6Сети
Под сетью мы будем понимать пару S = G, с,
где G = V, E — произвольный ориентированный граф, а с:
E R — функция, которая каждой дуге u, v ставит в соответствие неотрицательное вещественное число с(и, v), называемое пропускной способностью этой дуги. Множества V и Е называются соответственно множеством вершин и множеством дуг сети S.
Слайд 7Поток в сети
Потоком в сети S называется функция f, определенная
на E. Число f(u, v) называется потоком по дуге (u,
v). Более точно, говорят, что поток направлен от u к v, если f(u, v) > 0 и поток направлен от v к u, если f(u, v) < 0.
Будем для наглядности далее иметь в виду геометрическую реализацию сети и интерпретировать |f(u,v)| как постоянную скорость потока однородного вещества через дугу (u, v). Направление потока определяется знаком f(u, v)
Слайд 8Классификация вершин по воздействию на поток
Для произвольной функции f: E
R и произвольной вершины v сети S рассмотрим величину
Если f(u, v) мы интерпретируем как поток из и в v, то величина Divf (v) определяет «количество потока» (чистый поток), выходящего из вершины v. Эта величина может быть > 0 (если из вершины v больше выходит, чем входит в нее), < 0 (если в вершину входит больше, чем выходит из нее, т. е. наступает «накопление» потока в вершине v) и, наконец, = 0.
Вершина создает поток, поглощает или сохраняет.
Слайд 9 Сгруппируем вершины сети в множества V+, V– и
V0 следующим образом:
V+ = {v V| Div (v) >
0},
V– = {v V| Div (v) < 0},
V0 = {v V| Div (v) < 0}.
V+, V–. V0 называются источниками, стоками и промежуточными вершинами соответственно
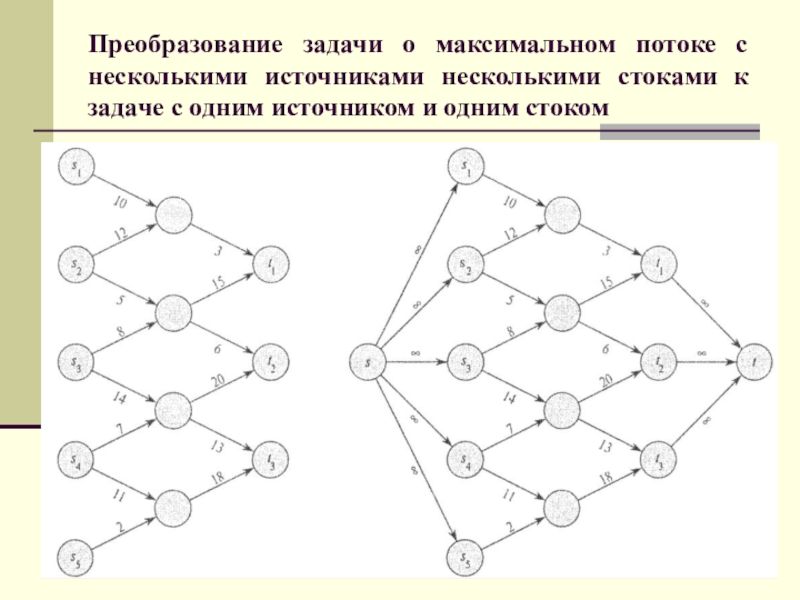
Слайд 10Преобразование задачи о максимальном потоке с несколькими источниками несколькими стоками
к задаче с одним источником и одним стоком
Слайд 11Величина потока
Выделим в нашей сети две вершины — источник, s
и сток t (s t).
Под потоком из s
в t в сети S мы будем понимать произвольную функцию вида f: E R, для которой выполняются условия
f(u, v) с(и, v) для каждой дуги u, v Е (ограничение пропускной способности),
f(u, v) = — f (v, u) (антисимметричность)
и
Div f (v) = 0 для каждой вершины v V \{s, t} (сохранение потока).
Величину W(f) = Div f (s) будем называть величиной потока f.
Слайд 12Под разрезом Р(А) сети S, соответствующим подмножеству А V
(А , А V), мы понимаем множество дуг
u, v Е, таких что u А и v V\A.
Для произвольного потока f в сети S поток через разрез Р(А) определяется естественным образом:
Слайд 13Лемма 1. Если s А и t V\A,
то для произвольного потока f из s в t
W(f) =
f(A, V\A) — f(V\A, A).
Доказательство. Суммируем уравнения Divf (v) = 0 для всех v А. Эта сумма складывается из некоторого числа слагаемых f(u, v), снабженных знаком плюс и минус, причем хотя бы одна из вершин и, v принадлежит множеству А. Если обе вершины принадлежат A, то f(u, v) появляется со знаком плюс в Divf(u) и со знаком минус в Divf(v) (и не появляется в выражении Divf(r) ни для одного r, отличного от и и v), что в сумме дает 0. Каждое из слагаемых f(u, v), и A, v V\A появляется в точности один раз со знаком плюс в Divf(u), что в сумме дает f(A, V\A). Аналогичные слагаемые f(u, v), и V\A, v A отвечают за слагаемое f(V\A, A). С другой стороны наша сумма равна Divf(s) = W(f), ибо Divf(v) = 0 для каждого v A\{s}.
Слайд 14Принимая A = V\{t}, получаем в этом частном случае из
леммы 1
Divf(s) = W(f) = f(V\{t}, {t}) – f({t}, V\{t}) =
=
– (f({t}, V\{t}) – f(V\{t}, {t})) = – Divf(t),
что выражает интуитивно понятный факт: в сток входит в точности такое количество потока, какое выходит из источника. В общем виде лемма 1 говорит, что общее количество потока можно измерить в произвольном разрезе, отделяющем s от t.
Слайд 15Определим пропускную способность разреза Р(А):
Под минимальным разрезом, разделяющим s и
t, мы будем понимать произвольный разрез Р(А), s
А, t V\A с минимальной пропускной способностью.
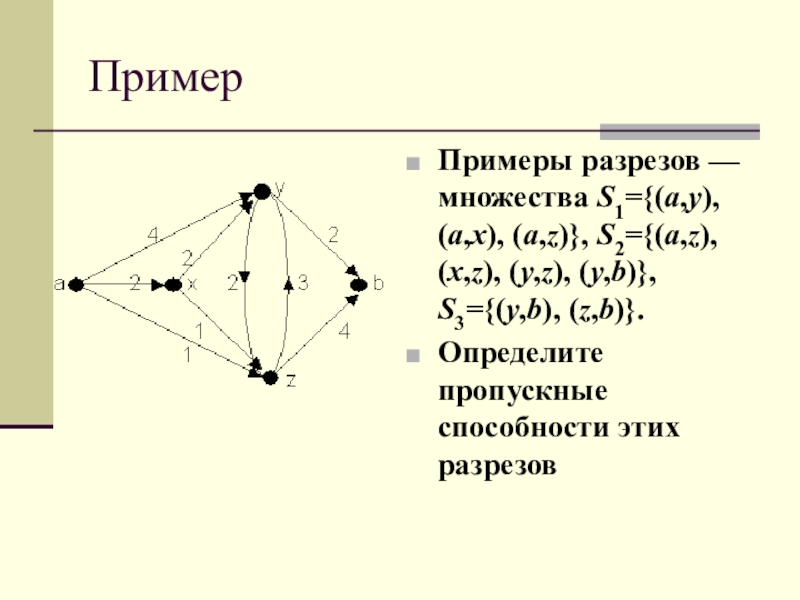
Слайд 16Пример
Примеры разрезов — множества S1={(a,y), (a,x), (a,z)}, S2={(a,z), (x,z), (y,z),
(y,b)}, S3={(y,b), (z,b)}.
Определите пропускные способности этих разрезов
Слайд 17Теорема (Форд и Фалкерсон).
Величина каждого потока из s в t
не превосходит пропускной способности минимального разреза, разделяющего s и t,
причем существует поток, достигающий этого значения.
Доказательство. Пусть Р(А) — минимальный разрез. В силу леммы 1 для произвольного потока f имеем
W(f) = f(A, V \A) – f(V \A, A) f(A, V \A) =
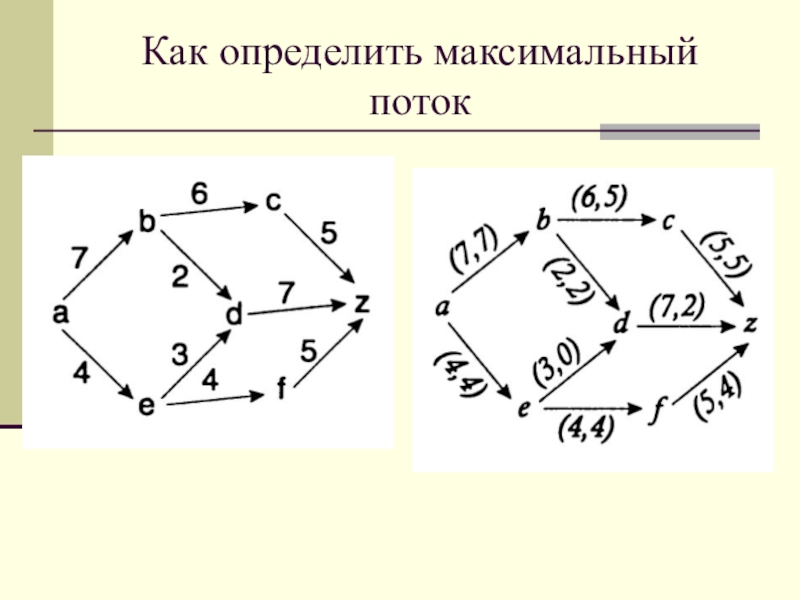
Слайд 18Как определить максимальный поток
Слайд 20Следует обратить внимание, что если поток из источника равен сумме
пропускных способностей ребер, выходящих из источника, или поток, втекающий в
сток, равен сумме пропускных способностей ребер, входящих в сток, то поток максимальный. Однако, поток может быть максимальным и без удовлетворения какого-либо из этих признаков.
Слайд 21Метод Форда-Фалкерсона
концепция остаточных сетей
концепция увеличивающих цепей
концепция разрезов
Метод является итеративным
Ford_Fulkerson_Method (G,
s, t)
Задаем начальное значение потока f равным 0
while существует увеличивающая
цепь p
do увеличиваем поток f вдоль цепи p
return f
Слайд 22Остаточные сети
Если задана некоторая сеть и поток, то остаточная сеть
— это сеть, состоящая из ребер, допускающих увеличение потока.
Пусть G
= V, E — сеть с источником s и стоком t. Величина дополнительного потока, который мы можем отправить из u в v, не превысив пропускную способность c(u,v), является остаточной пропускной способностью:
cf(u,v) = c(u, v) – f (u,v)
Слайд 23Для заданной сети G = V, E и потока f, остаточной
сетью, порожденной потоком f, является сеть Gf = V, Ef
, где
Ef = {(u,v) V V: cf(u,v) >0}.
Ребрами Ef являются или ребра E, или обратные им. Если f(u,v) 0 и (u,v) Ef . Если f (u,v) > 0 для некоторого ребра (u,v) E, то f (v, u) < 0. В таком случае cf(v, u) = c(v, u) – f (v, u) >0, и, следовательно, (v, u) Ef .
Слайд 25Метод увеличивающих цепей
Будем говорить, что дуга е сети S
является допустимой дугой из и в v относительно потока f,
если
е = и f(e) < c(e)
или
е = < v, u > и f(e) > 0.
В зависимости от того, какое из приведенных условий имеет место, первое или второе, будем говорить соответственно о согласованной или несогласованной допустимой дуге из и в v.
Слайд 26Увеличивающей цепью (длины l) для данного потока f из s
в t называется произвольная последовательность (попарно различных) вершин и дуг
v0,
e1, v1, e2,v2, …, vl–1, el, vl,
такая что v0 = s, vl = t, и для каждого i l дуга ei допустима из vi–1 в vi относительно потока f.
Знание увеличивающей цепи позволяет легко увеличить величину потока f на = min{(ei): 1 i l}, где
Слайд 27Для этого достаточно увеличить на поток по каждой согласованной
дуге ei:
а также уменьшить на поток по каждой несогласованной
дуге ei:
Для дуг е, не принадлежащих цепи полагаем f'(e)=f(e). Величина же потока увеличивается на :
W (f') = Divf’(s) = Divf(s) + = W (f') + .
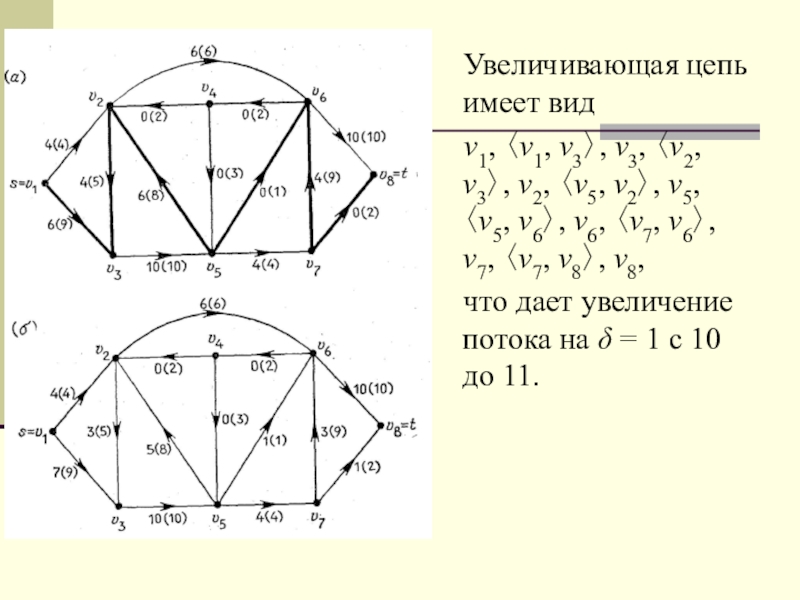
Слайд 28 Увеличивающая цепь имеет вид
v1, v1, v3,
v3, v2, v3, v2, v5, v2, v5, v5, v6, v6,
v7, v6, v7, v7, v8, v8,
что дает увеличение потока на = 1 с 10 до 11.
Слайд 29Теорема 3. Следующие три условия эквивалентны:
(а) Поток из s в
t максимален.
(б) Не существует увеличивающей цепи для f.
(в) W(f) =
c(A, V\A) для некоторого А V, такого что s A, t A.
Слайд 30Доказательство
(а) (б). Если поток максимален, то очевидно, что для
него не существует увеличивающей цепи, ибо существование такой цепи делало
бы возможным увеличение потока.
(б) (в). Предположим, что для некоторого потока f не существует увеличивающей цепи. Определим множество А V как множество вершин v, для которых существует цепь
v0, e1, v1, e2,v2, …, vk–1, ek, vk
такая что k 0, v0 = s, vk = v и еi — дуга, допустимая из vi-1 в vi, 1 i k. Очевидно, что s A, а t А, поскольку это означало бы существование увеличивающей цепи для f. Рассмотрим разрез Р(А). Для каждой дуги е Р(А) должно выполняться равенство f(e) = c(e) согласно определению множества А, таким образом, f(A, V\A) = c(A, V\A). Пользуясь определением множества А, аналогичным образом получаем f(V\A, A) = 0. В силу леммы 1 отсюда вытекает, что
W(f) = f(A, V \A) – f(V \A, A) = c(A, V\A).
(в) (а) следует из уже доказанного факта, что величина произвольного потока не превосходит с (A, V\A)
Слайд 31Алгоритм построения максимального потока
Идея метода: начиная с произвольного потока
(например, f(e) = 0 для каждой дуги е Е), мы ищем
увеличивающие цепи и увеличиваем вдоль них фактический поток.
1) Закончится ли работа такого алгоритма через конечное число шагов?
2) Будет ли полученный поток максимальным?
Слайд 32Ответ на второй вопрос будет утвердительным, что непосредственно следует из
теоремы 3.
Форд и Фалкерсон дали в некотором смысле отрицательный
ответ на первый вопрос. А именно, они привели пример сети, в которой можно так «злоумышленно» подбирать очередные рассматриваемые увеличивающие цепи, что процесс никогда не кончится; более того, величина потока в течение всего времени будет меньше одной четверти величины максимального потока.
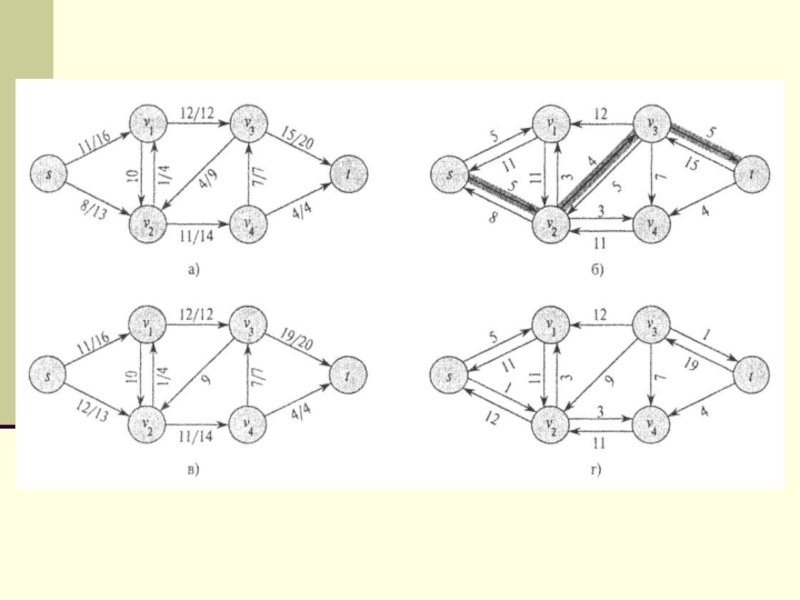
Слайд 35Алгоритм Эдмондса и Карпа
Эдмондс и Карп показали, что если
мы увеличиваем фактический поток всегда вдоль кратчайшей увеличивающей цепи, то
максимальный поток строится с использованием не более mn/2 цепей.
Отыскание кратчайшей цепи легко реализовать при помощи алгоритма, аналогичного поиску в ширину. Точнее говоря, начиная от источника s, мы ведем поиск в ширину в графе Gf, состоящем из дуг u, v, таких что в нашей сети существует дуга, допустимая от и до v относительного фактического потока f, вплоть до момента достижения стока t. Очевидно, что найденный в результате этого процесса кратчайший путь из s в t соответствует кратчайшей увеличивающей цепи из s в t в исходной сети. Принимая во внимание, что процесс поиска в ширину мы можем выполнить за время О(m + п), мы можем оценить сложность всего алгоритма построения максимального потока как О(тn(m + п)).
Слайд 36Алгоритм для построения максимального потока Диница
Этот метод основан на
построении некоторой вспомогательной бесконтурной сети, структура которой точно отображает все
кратчайшие увеличивающие цепи из s в t относительно фактического потока f. Обозначим такую сеть через Sf. Мы строим ее при помощи поиска в ширину в уже упомянутом графе Gf с дугами, определяемыми допустимыми относительно фактического потока f дугами в исходной сети. Сеть Sf содержит источник s, сток t и дуги графа Gf вида , где и находится на расстоянии d, a v на расстоянии d + 1 от s, 0 d l, где l есть длина сети Sf, т. е. расстояние от s до t в графе Gf. Пропускную способность cf(u, v) мы определяем как c(u,v) – f(u,v) или как f(v, u) в зависимости от того, представляет ли дуга согласованную дугу или нет (или сумму этих значений), если одновременно существуют согласованная и несогласованная дуги, допустимые от и к v.
Слайд 371 procedure PSA; (* построение вспомогательной бесконтурной сети Sf; переменные
V, XV, ПРЕДШ, ЗАПИСЬ, ХПРЕДШ, ХЗАПИСЬ, ДЛИНА, С, F, ХС,
XF, s, t — глобальные *)
2 begin
3 for u V do (* инициализация *)
4 begin ДЛИНА [и] := ; ХПРЕДШ [и] := ;
ХЗАПИСЬ[и]:= ;
5 for v V do ХС [и, v] := 0;
6 for v V do XF [u, v] := 0 (*инициализация нулевого потока*)
7 end;
8 ОЧЕРЕДЬ := ; XV := ; ДЛИНА [s] := 0;
(*поиск в ширину, начиная от источника s*)
9 ОЧЕРЕДЬ s;
10 while ОЧЕРЕДЬ do
11 begin u ОЧЕРЕДЬ; XV := XV {u};
12 for v ЗАПИСЬ [и] do (*поиск согласованных дуг*)
13 if (ДЛИНА [и] < ДЛИНА [v] ДЛИНА [t]) and (F [и, v] < С [и, v]) then
14 begin if ДЛИНА[и] = then ОЧЕРЕДЬ v; (*v — новая*)
15 ДЛИНА[v] := ДЛИНА[и] + 1;(*добавить к сети Sf*)
16 ХЗАПИСЬ[и] := ХЗАПИСЬ[и] {v};
17 ХПРЕДШ [v] := ХПРЕДШ[v] {u};
18 ХС[и, v] := С[и, v] – F[и, v]
19 end;
20 for v ПРЕДШ[и] do (*поиск несогласованных дуг*)
21 if (ДЛИНА[и] < ДЛИНА[v] ДЛИНА [t]) and (F[v, и] > 0) then
22 begin if ДЛИНА[v] = then ОЧЕРЕДЬ v; (* новый *)
23 ДЛИНА [v] := ДЛИНА[и] + 1;
24 if XC[и, v] = 0 then (* добавить к сети Sf *)
25 begin ХЗАПИСЬ[и] : = ХЗАПИСЬ[и] {v};
26 ХПРЕДШ[v] := ХПРЕДШ[v] {u};
27 end;
28 ХС[и, v] := XС[и, v] + F[и, v]
29 end
30 end
31 end

Слайд 38Эффективный алгоритм построения псевдомаксимального потока во вспомогательной бесконтурной сети (Малхотри,
Кумара и Махешвари)
Слайд 39Данные: Сеть, представленная списками инцидентности
ПРЕДШ [v], ЗАПИСЬ[v], v V,
пропускные способности c[u, v], и, v V, источник s
V и сток t V. Результаты: Максимальный поток F[u, v], и, v V.
1 begin
2 for u V do
3 for v V do F[и, v] := 0; (* нулевой начальный поток *)
4 repeat PSA; (*построение вспомогательной бесконтурной сети*)
5 if ДЛИНА[t] then (* поток F не является максимальным *)
begin MAXPSA; (*построение максимального потока
во вспомогательной сети*)
(*перенести поток из вспомогательной сети в главную*)
for u XV do (*XV = множество вершин вспомогательной
сети*)
8 for v XV do
9 begin F[u, v] := F[u, v] – XF[u, v];
10 if F[u, v] > C[u, v] then
11 begin
F[v, u] := F[v, u] – (F[u, v] – C[u, v]);
12 F[u, v] := C[u, v]
13 end
14 end
15 end (* конец фазы*)
16 until ДЛИНА[t] = (* поток F – максимальный *)
17 end






























![Потоки в сетях Данные: Сеть, представленная списками инцидентностиПРЕДШ [v], ЗАПИСЬ[v], v V, пропускные Данные: Сеть, представленная списками инцидентностиПРЕДШ [v], ЗАПИСЬ[v], v V, пропускные способности c[u, v], и, v ](/img/tmb/6/593726/012d473cf5858f48a8254301b73eab3d-800x.jpg)