Задачи урока:
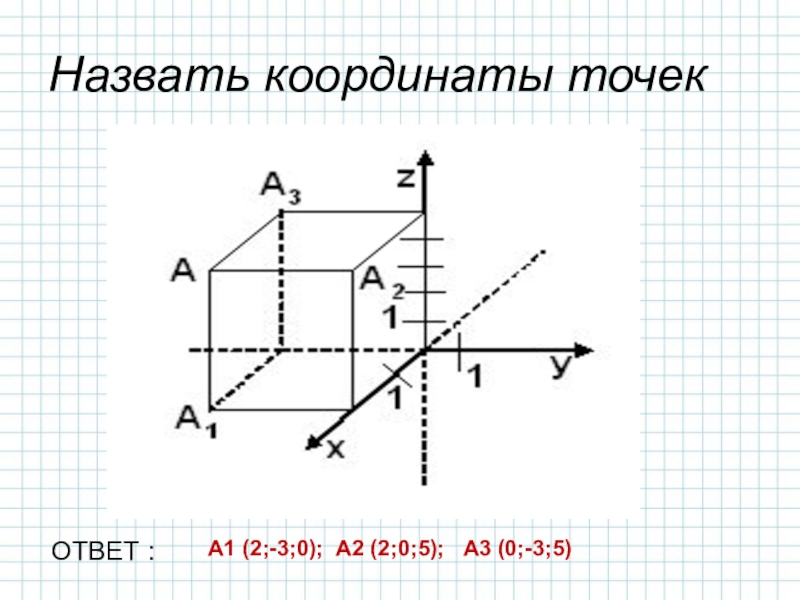
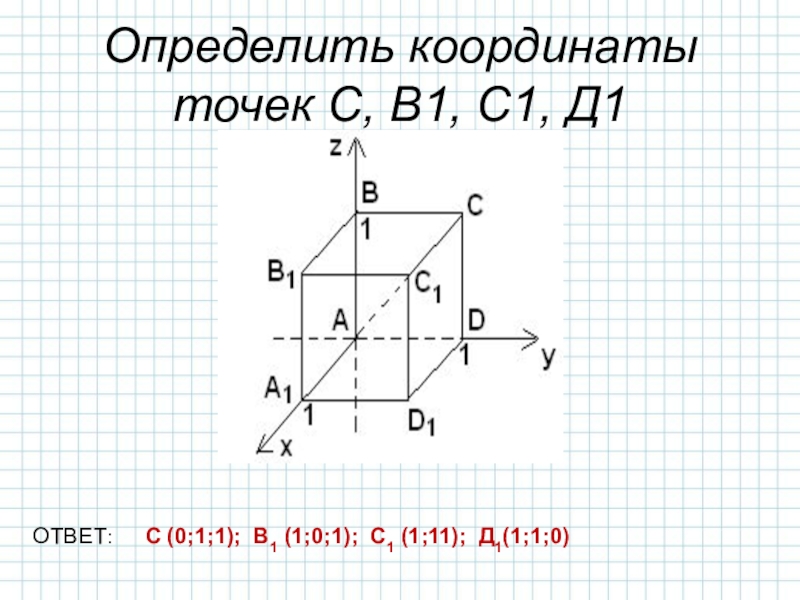
-вспомнить умения строить точку по заданным её
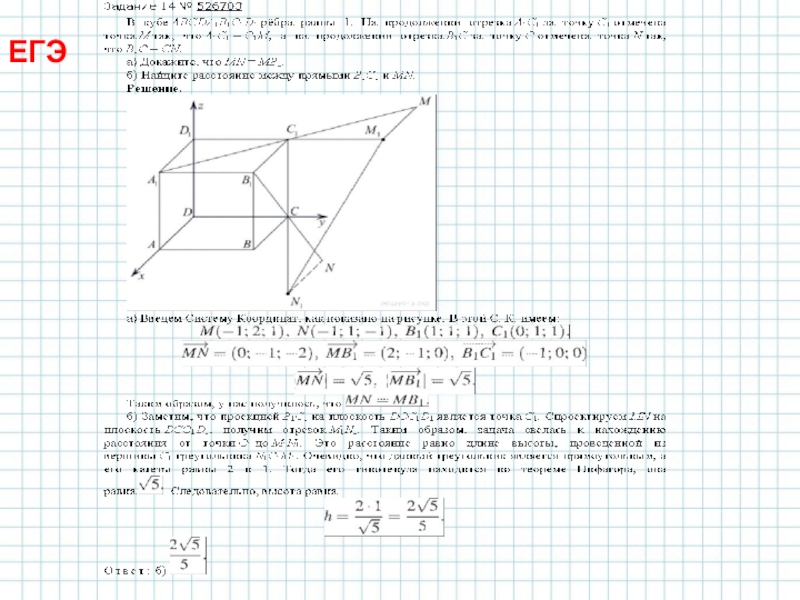
координатам и находить координаты точки, изображённой в заданной системе координат,-решить задачи ЕГЭ