Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПП12_1_Диффер_Теоремы_ан
Содержание
- 1. ПП12_1_Диффер_Теоремы_ан
- 2. МатематикаУГТУ-УПИ2007г.М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко, Н.М.Рыбалко, А.Б.СоболевПоточная практика 12.1 Дифференциал функции.Основные теоремы анализа
- 3. Цель:Изучить соответствующий математический аппарат для дальнейшего изучения
- 4. ОНК1, ОНК2, ОНК3: самостоятельная работа с литературой
- 5. Дифференциал функции.Основные теоремы анализа.
- 6. 1.Теоретическая часть2.Задачи3.Решения задач4.Упражнения5.Решение упражненийОглавлениеДифференциал функции.
- 7. Оглавление:Дифференциал функции. Дифференциал функции1.Определение дифференциала функции2.Свойства дифференциала3.Геометрический смысл
- 8. Дифференциал функции.Задача №:Оглавление:
- 9. Дифференциал функции.Решение задачи №:Оглавление:
- 10. Упражнение №:Оглавление:Основные теоремы анализа
- 11. Решение упражнения №:Оглавление:Основные теоремы анализа
- 12. Оглавление:Дифференциал функции
- 13. Оглавление:Дифференциал функции
- 14. Оглавление:Дифференциал функции
- 15. Оглавление:Дифференциал функции
- 16. Оглавление:Дифференциал функции
- 17. Оглавление:Дифференциал функции
- 18. Оглавление:Дифференциал функции
- 19. Оглавление:Дифференциал функции
- 20. Оглавление:Основные теоремы анализа
- 21. Оглавление:Основные теоремы анализа
- 22. Оглавление:Основные теоремы анализа
- 23. Оглавление:Основные теоремы анализа
- 24. Оглавление:Основные теоремы анализа
- 25. Оглавление:Основные теоремы анализа
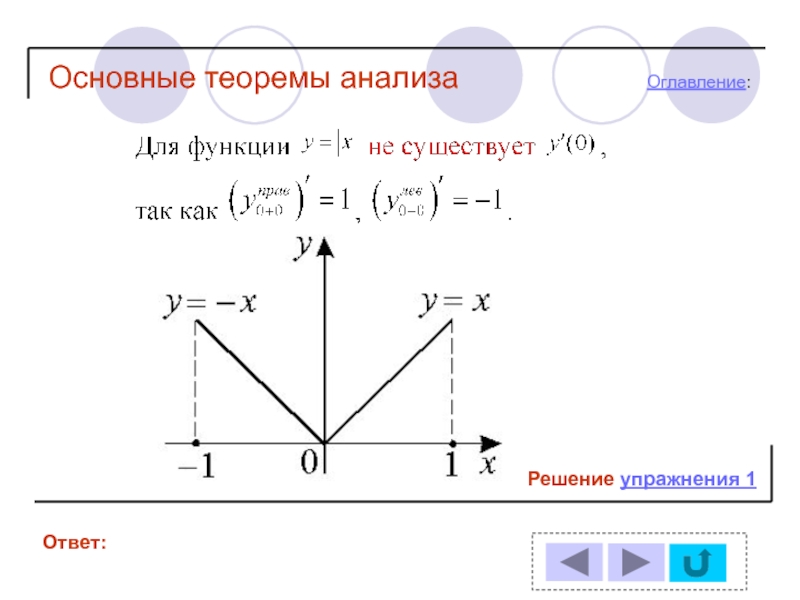
- 26. Упражнение 1Ответ: Решение:Оглавление:Основные теоремы анализа
- 27. Задача 1Ответ: Решение:Оглавление:Дифференциал функции
- 28. Ответ: Решение:Оглавление:Задача 2Дифференциал функции
- 29. Ответ: Решение:Оглавление:Задача 3Дифференциал функции
- 30. Ответ: 0,513Решение:Оглавление:Задача 4Дифференциал функции
- 31. Задача 5Ответ: 1,9938Решение:Оглавление:Дифференциал функции
- 32. Задача 6Ответ: 443Решение:Оглавление:Дифференциал функции
- 33. Решение упражнения 1Ответ:Оглавление:Основные теоремы анализа
- 34. Решение задачи 1Ответ:Оглавление:Дифференциал функции
- 35. Решение задачи 2Ответ:Оглавление:Дифференциал функции
- 36. Решение задачи 3Ответ:Оглавление:Дифференциал функции
- 37. Решение задачи 4Ответ: 0,513Оглавление:Дифференциал функции
- 38. Решение задачи 5Ответ: 1,9938Оглавление:Дифференциал функции
- 39. Решение задачи 6Ответ: 443Оглавление:Дифференциал функции
- 40. В результате студент должен уметь:1. Вычислять дифференциалы
- 41. Перечень источников, список дополнительной литературы по теме.Сборник
- 42. Скачать презентанцию
МатематикаУГТУ-УПИ2007г.М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко, Н.М.Рыбалко, А.Б.СоболевПоточная практика 12.1 Дифференциал функции.Основные теоремы анализа
Слайды и текст этой презентации
Слайд 2Математика
УГТУ-УПИ
2007г.
М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко,
Н.М.Рыбалко, А.Б.Соболев
Поточная практика 12.1
Слайд 3Цель:
Изучить соответствующий математический аппарат для дальнейшего изучения курса математики и
применять методы математического анализа в ходе изучения специальных дисциплин для
будущей профессиональной деятельности.
Слайд 4ОНК1, ОНК2, ОНК3: самостоятельная работа с литературой и электронными изданиями
для поиска информации об отдельных определениях, понятиях и терминах, объяснения
их применения в практических ситуациях, решения теоретических и практических типовых и системных задач, связанных с дальнейшим изучением курса математики и специальных дисциплин.ИК1: способность самостоятельно работать на компьютере;
ИК2: выполнение расчетов в ходе последующего обучения;
ИК4: готовность работать с информацией из разных источников.
Формируемые общенаучные, инструментальные и индивидуальные компетенции по ФГОС:
ИД3,5: навыки логического творческого и системного мышления .
Слайд 61.Теоретическая часть
2.Задачи
3.Решения задач
4.Упражнения
5.Решение упражнений
Оглавление
Дифференциал функции.
Слайд 7Оглавление:
Дифференциал функции.
Дифференциал функции
1.Определение дифференциала функции
2.Свойства дифференциала
3.Геометрический смысл дифференциала
4.Применение дифференциала
к
приближенным вычислениям
5.Дифференциалы высших порядков
Основные теоремы анализа
6.Теорема Ролля
7.Теорема Лагранжа
8.Теорема Коши
Слайд 40В результате студент должен уметь:
1. Вычислять дифференциалы первого и более
высокого порядка.
2. Применять понятие дифференциала
к приближенным вычислениям.
3. Пользоваться основными
теоремами анализа.
Слайд 41Перечень источников,
список дополнительной литературы по теме.
Сборник задач по математике
для втузов: В 4 ч. Ч. 2: Введение в анализ.
Дифференциальное и интегральное исчисление функций одной переменной. Дифференциальное исчисление функций нескольких переменных. Кратные интегралы. Дифференциальные уравнения./ А. В. Ефимов, А. Ф. Каракулин, И. Б. Кожухов и др. / Под ред. А. В. Ефимова, А. С. Поспелова. - 4-е изд., перераб. и доп. - М.: Физматлит, 2003. - 288 с.: ил.; 21 см. - ISBN 5-940520-34-0.2. Данко, Павел Ефимович. Высшая математика в упражнениях и задачах: Учеб. пособие для вузов: В 2 ч. Ч. 1 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд. - М.: ОНИКС 21 век : Мир и образование, 2003. - 304с.: ил.; 22 см. - ISBN 5-329-00326-1.
3. Кузнецов, Леонид Антонович. Сборник задач по высшей математике. Типовые расчеты: учеб. пособие / Л. А. Кузнецов. - Изд. 3-е, испр. –
СПб. ; М. ; Краснодар: Лань, 2005. - 240 с.; 21 см. - (Учебники для вузов. Специальная литература). - Загл. 1-го изд.: Сборник заданий по высшей математике: Типовые расчеты. - ISBN 5-8114-0574-X.
