Практическое занятие 6

оценки его результатов
Задание
1. Определить коэффициенты линейной множественной регрессии.
2. Определить

дисперсии (общая, факторная, остаточная) и корреляционную связь признака и факторов.
3. Определить коэффициент детерминации и множественный R.
4. Определить критерий Фишера и ошибки аппроксимации.
5. Определить t критерий и границы доверительной вероятности.
6. Произвести оценку значений определенных параметров.
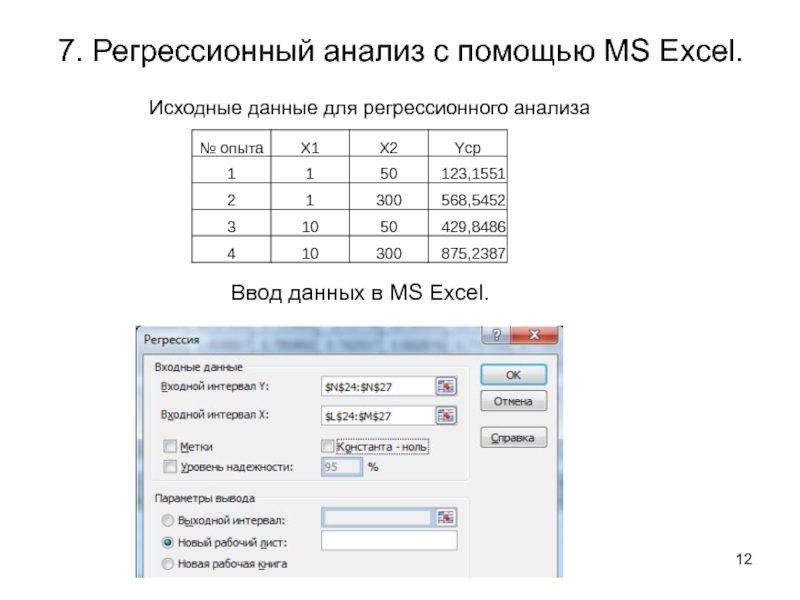
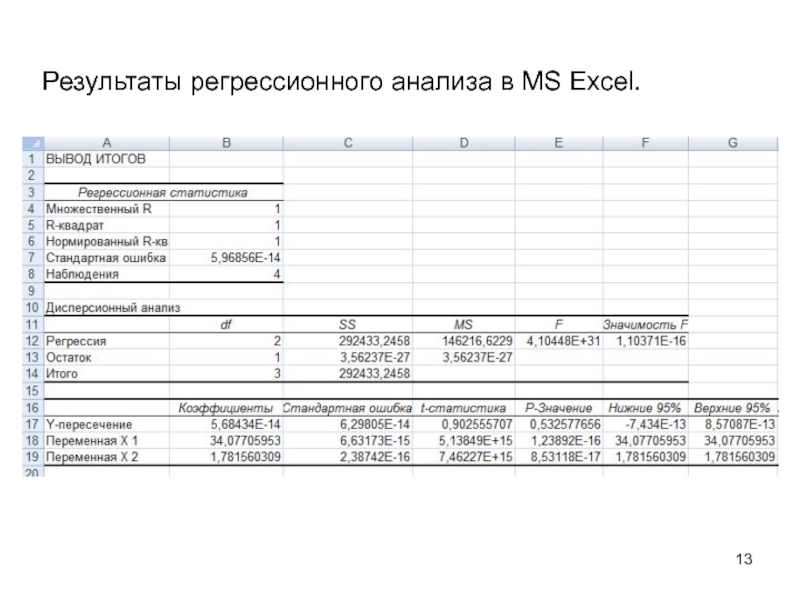
7. Провести регрессионный анализ с помощью MS Excel.
8. Сделать выводы по работе.

модели необходимо определить коэффициенты уравнения регрессии b0 , b1 и

b2. решим систему трехлинейных уравнений с тремя неизвестными b0,b1,b2: 





Для решения системы можете воспользоваться решение системы методом Крамера

значений строим функцию

дисперсия результативного признака Y, отображающую влияние как основных, так и

остаточных факторов:




где - среднее значение результативного признака Y.

дисперсия результативного признака Y, отображающую влияние только остаточных факторов




При корреляционной

связи результативного признака и факторов выполняется соотношение


при этом

линейной многофакторной регрессии используют множественный коэффициент детерминации





Множественный R равен

квадратному корню из коэффициента детерминации, эта величина принимает значения в интервале от нуля до единицы.

число наблюдений;
m – число факторов в

уравнении регрессии.
Показатель средней ошибки аппроксимации

аппроксимации



где - стандартное значение ошибки для коэффициента

регрессии
Границы доверительных интервалов для коэффициентов регрессии

к 1.
2) Проверка значения критерия Фишера - должен быть в

интервале(Fкр;+∞), определяется в Excel =FРАСПОБР(0,05;кп;ко)
3) Оценка значимости – значение должно быть меньше 0,05.
4) Проверка t-критерия - должен попадать в критическую область: (-∞;tкр)U(tкр;+ ∞). Определяется: =СТЬЮДРАСПРОБР(0,05; n-k-1).
5) Проверка нижних и верхних границ доверительных интервалов - не должен проходить через 0.

Excel.
Исходные данные для регрессионного анализа

и с помощью MS Excel. Далее сравниваем полученные результаты. Даем

рекомендации по использованию моделей для прогнозирования.