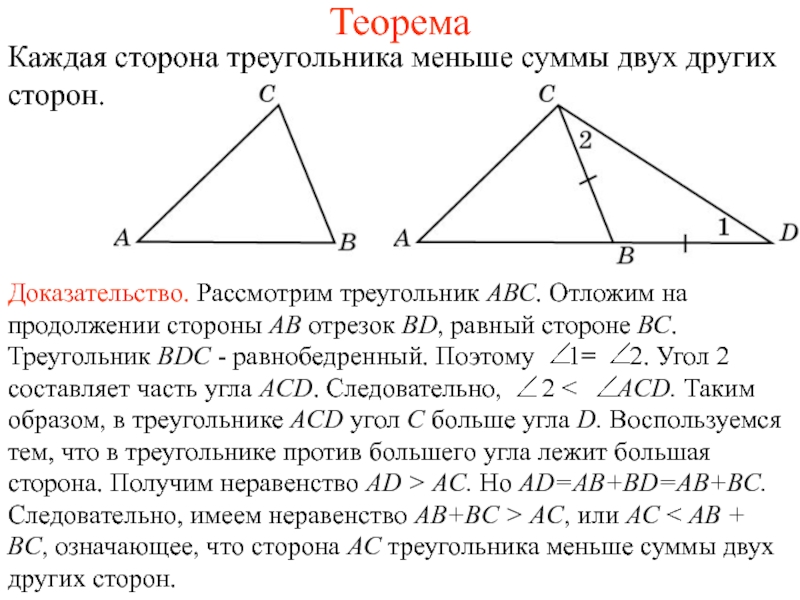
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Практическое занятие №1 Корреляционный анализ
Содержание
- 1. Практическое занятие №1 Корреляционный анализ
- 2. План занятия1. Корреляционный анализ. 2. Проверка гипотез о взаимосвязи переменных.
- 3. ПримерыМенеджер интересуется, зависит ли объем продаж в
- 4. Постановка проблемыНаша цель – научиться отвечать на
- 5. Корреляционный анализэто совокупность основанных на математической теории
- 6. Корреляция и причинная связьКогда проверка гипотезы показывает,
- 7. Корреляционные связиПо форме корреляционная связь может быть
- 8. Корреляционные связиположительная корреляция (большие значения одного набора
- 9. Величина (сила) связи и ее значимость (достоверность)
- 10. Коэффициенты корреляцииКоэффициент корреляции Браве-Пирсона (r) — это
- 11. Коэффициент корреляцииКоэффициент корреляции измеряет силу и направление
- 12. Коэффициент корреляцииКоэффициент корреляции — это величина, которая
- 13. Допущения для определения коэффициента корреляцииМетрический характер измеряемых
- 14. Значения коэффициента корреляцииКоэффициент корреляции изменяется на отрезке
- 15. Корреляционные связиЦихончик Н.В., 2016
- 16. Цихончик Н.В., 2016
- 17. Слайд 17
- 18. Корреляционный анализВыбрать коррелируемые переменные (интервальная шкала, нормальное распределение)Гипотеза о связи переменныхКорреляционная матрицаКоэффициенты корреляцииКорреляционная плеяда
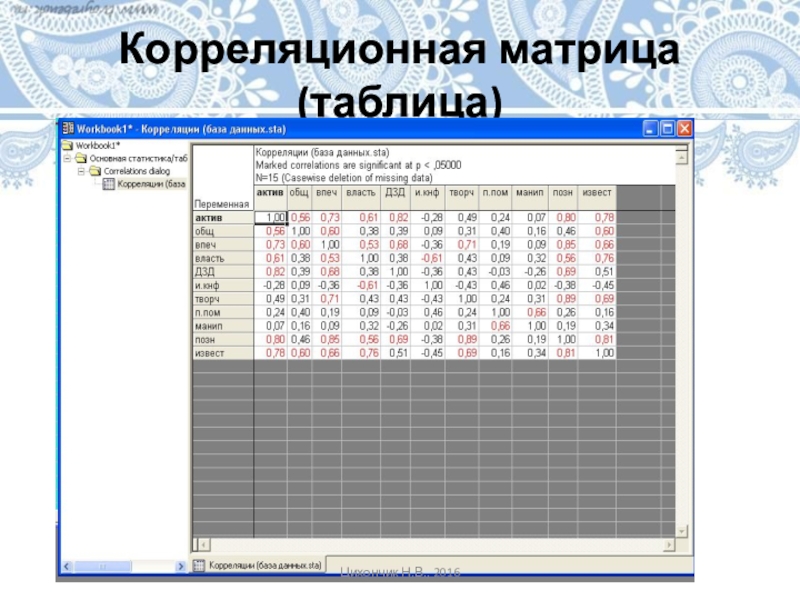
- 19. Корреляционная матрица (таблица)Цихончик Н.В., 2016
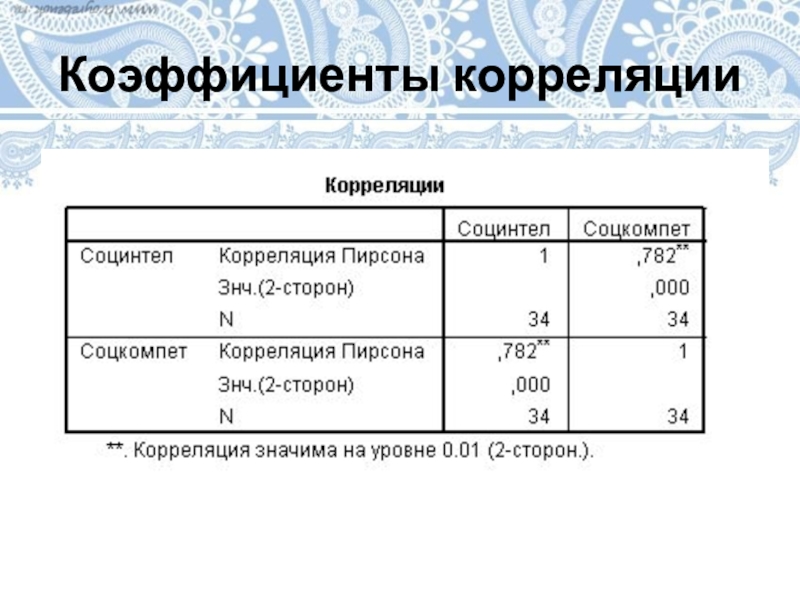
- 20. Коэффициенты корреляции
- 21. Корреляционная плеядакорреляционные плеяды – это способ отображения
- 22. Корреляционная плеядаЦихончик Н.В., 2016
- 23. 2 задача занятия – Проверка гипотез о взаимосвязи переменных
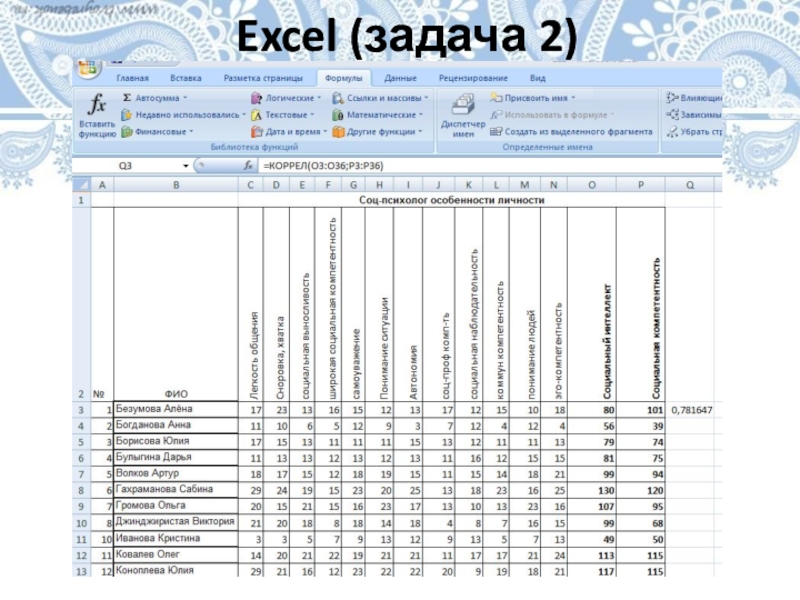
- 24. Excel (задача 2)
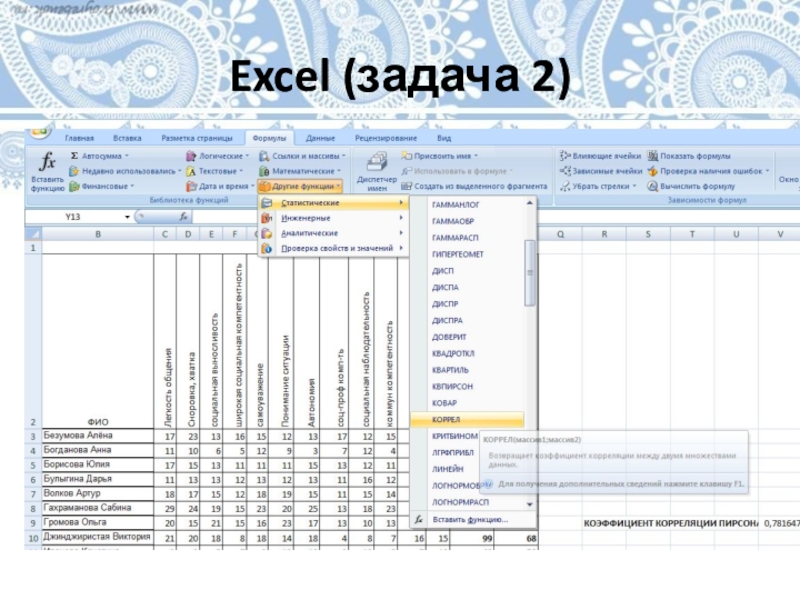
- 25. Excel (задача 2)
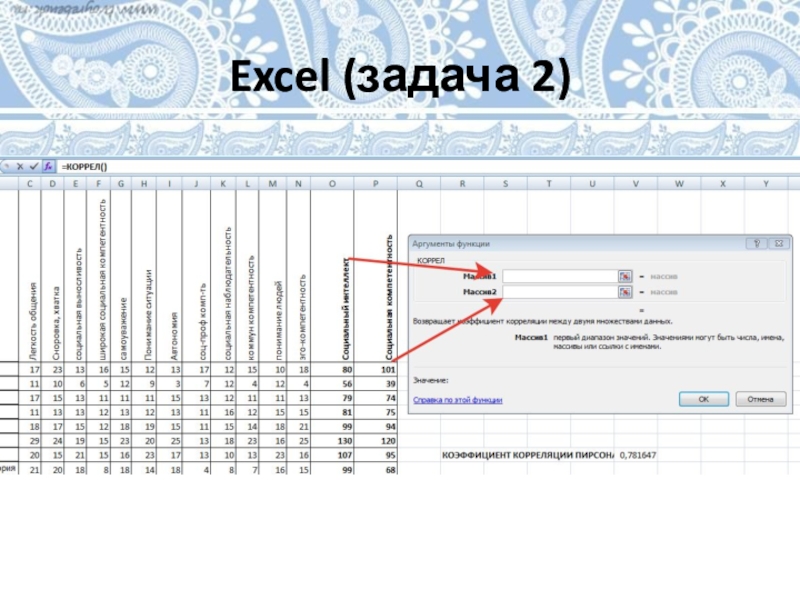
- 26. Excel (задача 2)
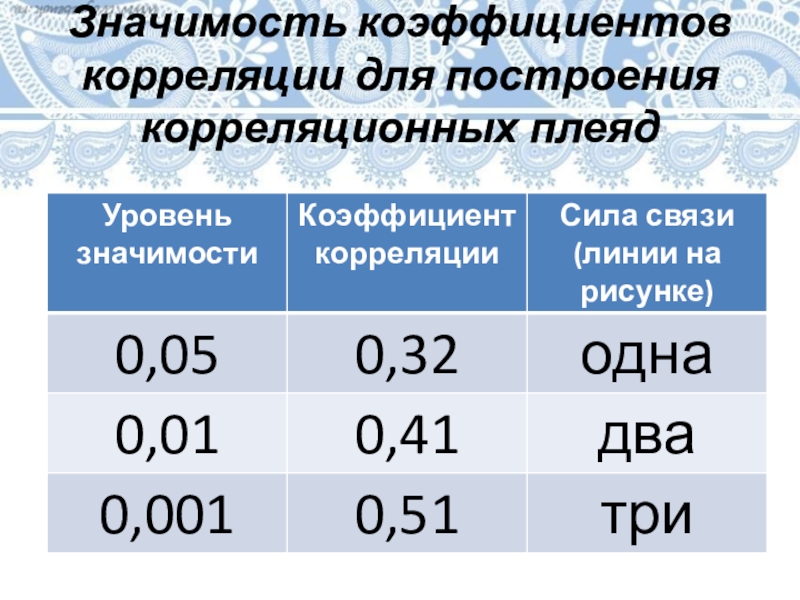
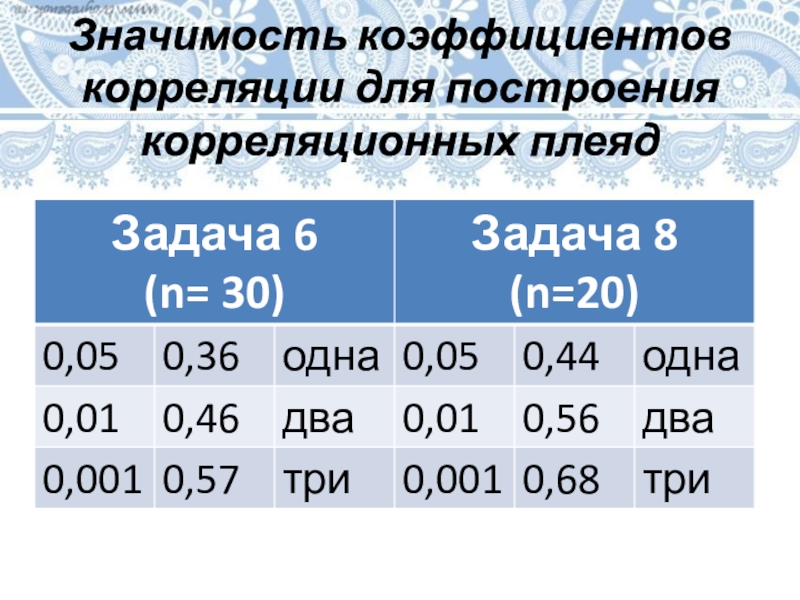
- 27. Значимость коэффициентов корреляции для построения корреляционных плеяд
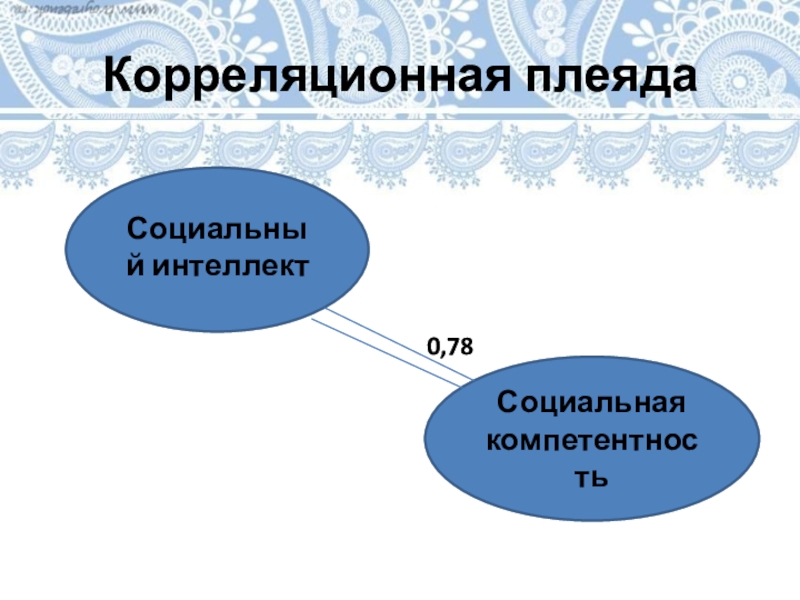
- 28. Корреляционная плеядаСоциальный интеллектСоциальная компетентность0,78
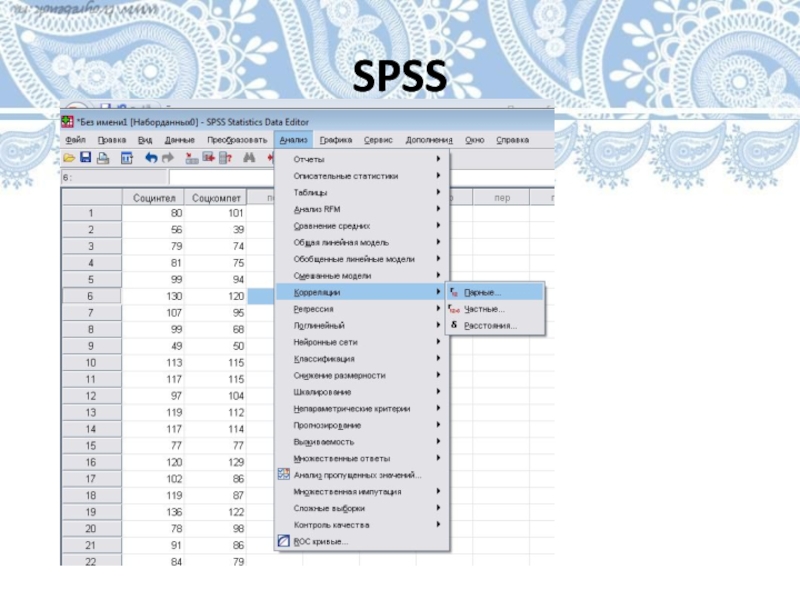
- 29. SPSS
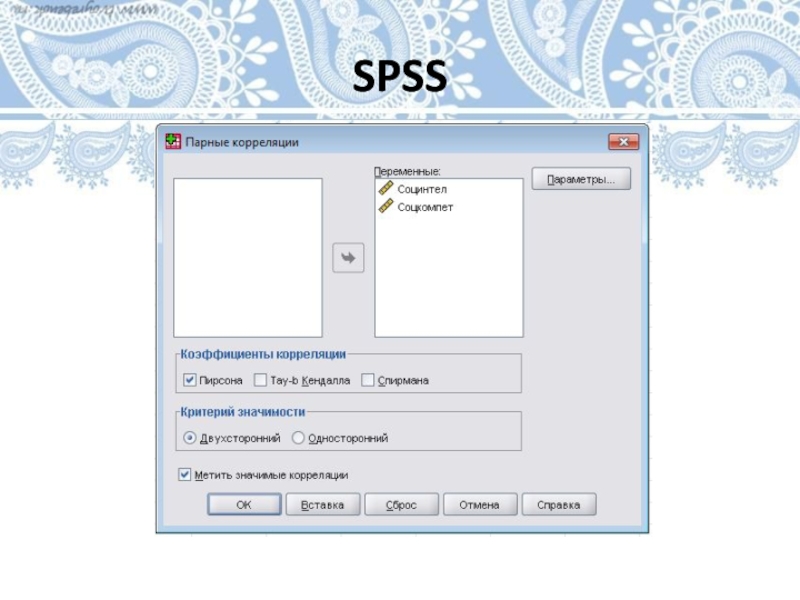
- 30. SPSS
- 31. Задания (Файл 111. xls)Задача 6. Построить корреляционные
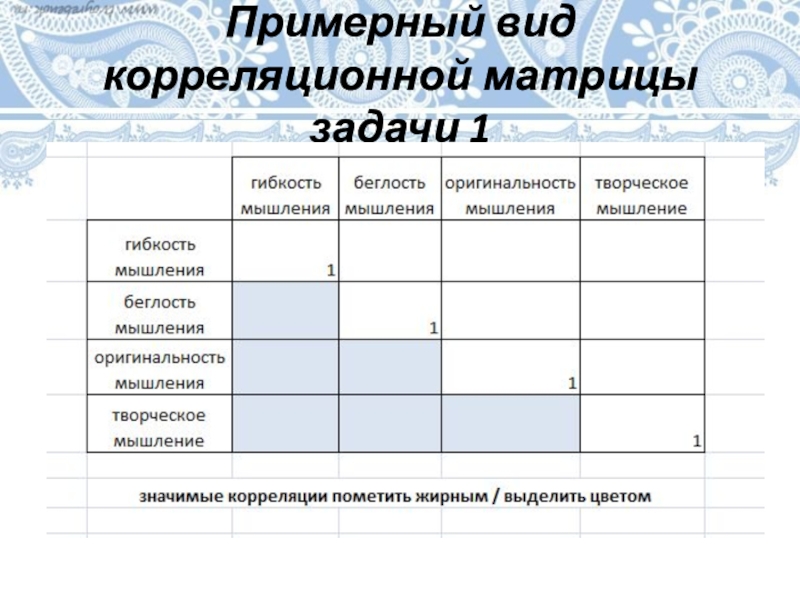
- 32. Примерный вид корреляционной матрицы задачи 1
- 33. Значимость коэффициентов корреляции для построения корреляционных плеяд
- 34. Итог занятияПо результатам решения задач необходимо сдать
- 35. Задание к следующему занятиюКластерный анализ: понятие и назначение процедуры.Виды кластерного анализа.
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Практическое занятие №1
«Корреляционный анализ»
по дисциплине «Многомерный статистический анализ в социологических
исследованиях»
Слайд 3Примеры
Менеджер интересуется, зависит ли объем продаж в этом месяце от
объема рекламы в этом же периоде?
Преподаватель хочет выяснить, есть ли
зависимость между количеством часов, потраченных студентом на занятия, и результатами экзамена?Врач исследует, влияет ли кофеин на сердечные болезни и существует ли связь между возрастом человека и его кровяным давлением?
Социолог исследует, какова связь между уровнем преступности и уровнем безработицы в регионе? Есть ли зависимость между расходами на жилье и совокупным доходом семьи? Связаны ли доход от профессиональной деятельности и продолжительность образования?
Цихончик Н.В., 2016
Слайд 4Постановка проблемы
Наша цель – научиться отвечать на четыре вопроса:
Вопрос 1.
Существует ли связь между двумя или более переменными?
Вопрос 2. Какой
тип имеет эта связь? Вопрос 3. Насколько она сильна?
Вопрос 4. Какой можно сделать прогноз, основываясь на этой связи?
Цихончик Н.В., 2016
Слайд 5Корреляционный анализ
это совокупность основанных на математической теории корреляции методов обнаружения
корреляционной зависимости между двумя случайными признаками или факторами
это проверка гипотез
о связях между переменными с использованием коэффициентов корреляции«Оба термина, — пишет Е.В. Сидоренко, — корреляционная связь и корреляционная зависимость — часто используются как синонимы. Зависимость подразумевает влияние, связь — любые согласованные изменения, которые могут объясняться сотнями причин»
Цихончик Н.В., 2016
Слайд 6Корреляция и причинная связь
Когда проверка гипотезы показывает, что существует значимая
линейная связь между переменными, исследователь должен рассмотреть возможные виды связи
между переменными и выбрать ту, которая диктуется логикой исследования.Цихончик Н.В., 2016
Слайд 7Корреляционные связи
По форме корреляционная связь может быть прямолинейной или криволинейной
По
направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной")
Степень,
сила или теснота корреляционной связи определяется по величине коэффициента корреляцииЦихончик Н.В., 2016
Слайд 8Корреляционные связи
положительная корреляция (большие значения одного набора связаны с большими
значениями другого)
отрицательная корреляция (малые значения одного набора связаны с большими
значениями другого)нулевая корреляция (данные двух наборов никак не связаны)
Цихончик Н.В., 2016
Слайд 9Величина (сила) связи и ее значимость (достоверность) представляют две различные
характеристики связи. В общем случае, чем сильнее связь, тем более
значимой она являетсяНулевая гипотеза утверждает, что для генеральной совокупности, из которой была извлечена выборка, связь между переменными полностью отсутствует, т.е. значение проверяемого показателя меры связи для генеральной совокупности равно нулю
Дальнейшая логика проверки на статистическую значимость аналогична общей последовательности этапов проверки любой статистической гипотезы
Цихончик Н.В., 2016
Слайд 10Коэффициенты корреляции
Коэффициент корреляции Браве-Пирсона (r) — это параметрический показатель, для
вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений
Коэффициент
корреляции рангов Спирмена (rs) — это непараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измеренийЦихончик Н.В., 2016
Слайд 11Коэффициент корреляции
Коэффициент корреляции измеряет силу и направление связи между двумя
переменными.
Обозначения:
Выборочный коэффициент корреляции r
Коэффициент корреляции генеральной совокупности ρ
Цихончик
Н.В., 2016Слайд 12Коэффициент корреляции
Коэффициент корреляции — это величина, которая может варьировать в
пределах от +1 до -1 (т.е. -1 < r
1)Коэффициенты корреляции — удобный показатель связи
по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками
Таблицы значений критериев можно найти в специальных руководствах
Цихончик Н.В., 2016
Слайд 13Допущения для определения коэффициента корреляции
Метрический характер измеряемых данных (данные представлены
в интервальной шкале или шкале отношений)
Обе переменные подчиняются нормальному закону
распределенияЗависимость между переменными приблизительно линейна
Гомоскедастичность, т.е. однородность дисперсий (дисперсия значений y равномерна для всех значений x). На графике значения y должны быть приблизительно равномерно распределены выше и ниже линии y(x) по всей ее длине (точки на графике должны образовывать достаточно симметричную овалообразную форму без значительных выбросов)
Существенные признаки нелинейности или отклонения от гомоскедастичности свидетельствуют о необходимости использовать другую меру связи и другой критерий значимости.
Цихончик Н.В., 2016
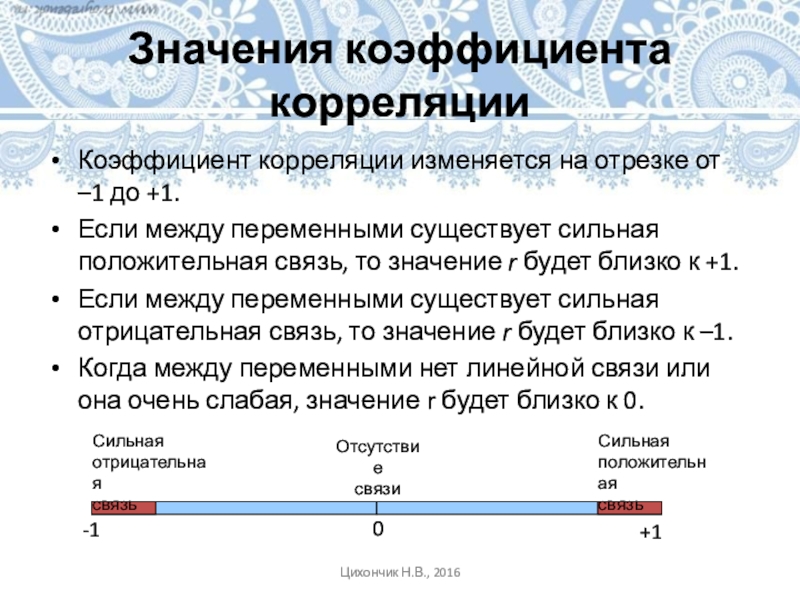
Слайд 14Значения коэффициента корреляции
Коэффициент корреляции изменяется на отрезке от –1 до
+1.
Если между переменными существует сильная положительная связь, то значение
r будет близко к +1. Если между переменными существует сильная отрицательная связь, то значение r будет близко к –1.
Когда между переменными нет линейной связи или она очень слабая, значение r будет близко к 0.
-1
+1
0
Сильная
отрицательная
связь
Сильная
положительная
связь
Отсутствие
связи
Цихончик Н.В., 2016
Слайд 18Корреляционный анализ
Выбрать коррелируемые переменные (интервальная шкала, нормальное распределение)
Гипотеза о связи
переменных
Корреляционная матрица
Коэффициенты корреляции
Корреляционная плеяда
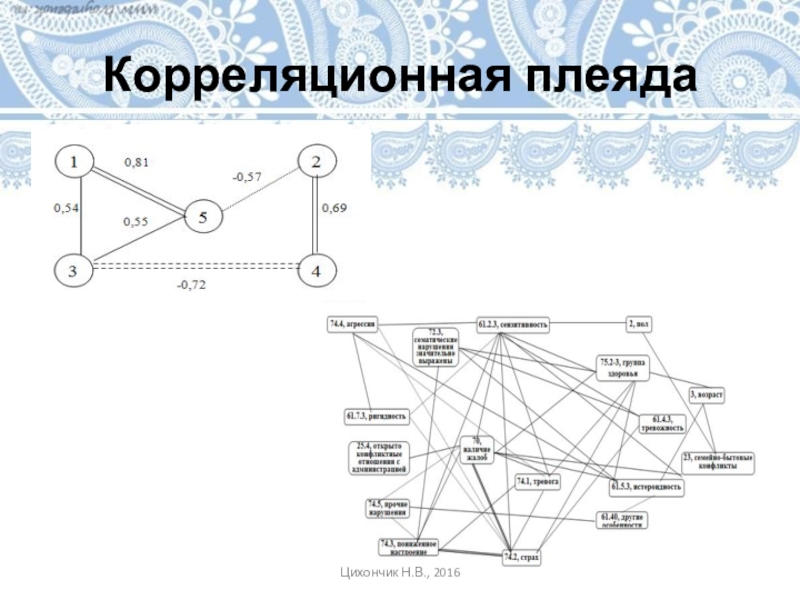
Слайд 21Корреляционная плеяда
корреляционные плеяды – это способ отображения информации о корреляциях,
который помогает их структурировать, проводить объединение коррелирующих факторов
http://www.robotron.ru/papers/pleyadi.html Примеры удачных
и неудачных построений плеядЦихончик Н.В., 2016
Слайд 31Задания (Файл 111. xls)
Задача 6. Построить корреляционные плеяды для групп
1 и 2.
Задача 8. Построить корреляционные плеяды для групп 1
и 2 по 5 стратегиям поведения в конфликте.Задача 10. Установить значимые корреляции успеваемости с показателями теста.